SVEUCILIŠTE J. J. STROSSMAYERA U OSIJEKUODJEL ZA MATEMATIKU

PREDDIPLOMSKI STUDIJ MATEMATIKE

Tajana Novak

Mersennovi i savršeni brojeviZavršni rad

Osijek, 2014.

SVEUCILIŠTE J. J. STROSSMAYERA U OSIJEKUODJEL ZA MATEMATIKU

PREDDIPLOMSKI STUDIJ MATEMATIKE

Tajana Novak

Mersennovi i savršeni brojeviZavršni rad

Voditelj: doc. dr. sc. Ivan Matic

Osijek, 2014.

Sažetak: Ovaj završni rad proucava kakav oblik imaju elementi nekih podskupovaskupa prirodnih brojeva (Mersennovi i savršeni brojevi). Uz kratak prikaz povijesti vi-djeti cemo kako je došlo do otkrica novih brojeva te objasniti u kakvom su odnosu Mer-sennovi i savšeni brojevi. U 17. stoljecu brojeve oblika 2p− 1, gdje je p prost broj,pocinje izucavati francuski redovnik Marin Mersenne (1588. – 1648.). Ti brojevi su ponjemu dobili ime Mersennovi brojevi. Ako je broj Mp = 2p− 1 prost broj, onda se onnaziva Mersennov prost broj. Uz Mersennove brojeve vežemo savršene brojeve. To subrojevi koji imaju osobinu da su jednaki zbroju svojih pravih djelitelja. Traženje i jednihi drugih matematicarima je zadavalo velike poteškoce.

Kljucne rijeci: Marin Mersenne, Mersennovi brojevi, Mersennovi prosti brojevi, savr-šeni brojevi

Abstract: This final paper studies the form that the elements of some subsets of thenatural numbers set have (Mersenne and perfect numbers). After a brief history reviewwe can see how there has been a discovery of new elements and explain the relationshipbetween Mersenne and perfect numbers. In the 17th century the French monk MarinMersenne (1588th-1648th) begins to study numbers of form 2p− 1 where p is a primenumber. These numbers are named after him and called Mersenne numbers. If the num-ber of Mp = 2p− 1 is a prime number, then it is called Mersenne prime number. WithMersenne numbers we associate perfect numbers. These are numbers that have a charac-teristic that they are equal to the sum of their aliquot divisors. Search for both of themhas caused great difficulties for mathematicians.

Key words: Marin Mersenne, Mersenne numbers, Mersenne primes, perfect numbers

Sadržaj

1 Uvod 3

2 Pregled povijesti 4

2.1 Marin Mersenne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.2 Razvoj znanosti u 17. stoljecu . . . . . . . . . . . . . . . . . . . . . . . 4

3 Mersennovi brojevi 7

3.1 Definicija i osnovna svojstva . . . . . . . . . . . . . . . . . . . . . . . . 7

3.2 Potraga za Mersennovim brojevima . . . . . . . . . . . . . . . . . . . . 8

3.3 Neka svojstva Mersennovih brojeva . . . . . . . . . . . . . . . . . . . . 10

4 Savršeni brojevi 13

4.1 Definicija i osnovna svojstva . . . . . . . . . . . . . . . . . . . . . . . . 13

4.2 Parni savršeni brojevi . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

4.3 Neka svojstva parnih savršenih brojeva . . . . . . . . . . . . . . . . . . . 17

1 Uvod

Za razvoj znanosti u 17. stoljecu znacajnu ulogu imala su tri udruženja: Acca-demia dei Lincei u Rimu, koja je postojala samo kratko vrijeme, Académie Royale desSciences u Parizu, te Royal Society u Londonu. Za osnivanje Académie Royale des Sci-ences je zaslužan Marin Mersenne. Poznati Philosophical Transactions, kojega je RoyalSociety poceo izdavati 1665., i The Journal des Savants su bili prvi casopisi u kojima suse objavljivali matematicki i znanstveni clanci.

U 17. stoljecu brojeve oblika 2p− 1 , gdje je p prost broj, pocinje izucavati fran-cuski redovnik Marin Mersenne (1588. – 1648.). Mersenne je bio matematicar, fizicar,filozof, teoreticar muzike i teolog. Bio je centralna licnost jedne od najznacajnijih na-ucnih grupa u Francuskoj pocetkom 17. stoljeca. Ti brojevi su po njemu dobili imeMersennovi brojevi. Ako je broj Mp = 2p− 1 prost broj, onda se on naziva Mersennovprost broj. Mersenne je u svojoj knjizi Cogitata physico mathematica 1644. godine izniotvrdnju da je Mp prost broj za p = 2,3,5,7,13,17,19,31,67,127,257 te da je Mp složenza sve ostale proste brojeve p < 257. Kasnija istraživanja pokazala su da je napravio petpogrešaka. Do danas su poznata 48 Mersennova prosta broja, ali su toliko brzo rastuci dasu danas deset najvecih poznatih prostih brojeva upravo Mersennovi brojevi.

Uz Mersennove brojeve vežu se savršeni brojevi. To su brojevi koji imaju svojstvoda su jednaki zbroju svojih pravih djelitelja. Najmanji takav je broj 6 i za njega vrijedida je zbroj njegovih pravih djelitelja jednak 1+2+3 = 6 , pa je to savršen broj. Još nijepoznato postoje li neparni savršeni brojevi. Za parne je formulu još davno dao Euklid,a nadopunio ga je Euler pa danas znamo da ako je 2p−1 Mersennov prost broj, onda je2p−1(2p−1) paran savršen broj.

Vidimo da je traženje parnih savršenih brojeva direktno povezano sa traženjemMersennovih prostih brojeva, pa je traženje i jednih i drugih zadavalo poteškoce mate-maticarima kroz povijest.

3

2 Pregled povijesti

2.1 Marin Mersenne

Marin Mersenne je roden u radnickoj obitelji u malom gradu Oizé u pokrajini Ma-ine (današnji Sarthe, Francuska) 8. rujna 1588. godine i kršten je na isti dan. Od malihnogu pokazivao je želju za proucavanjem. Bez obzira na financijsku situaciju, Marina suroditelji poslali u Le Mans gdje je ucio gramatiku. Kasnije, u dobi od šesnaest godina,Mersenne je zatražio da ide u novoosnovanu isusovacku školu College La Fleche, u kojuje takoder bio upisan i Descartes, koji je osam godina mladi od Mersenna. Mersennovotac je želio da mu sin ima crkvenu karijeru, medutim Mersenne je bio posvecen studijukoji je volio i spreman za vece odgovornosti, odlucio se na daljnje školovanje u Parizu.Krenuvši u Pariz, na putu je boravio u samostanu Minims. To iskustvo je toliko inspiri-ralo Mersenna tako da je obecao pridružiti se njihovom redu ako se jednoga dana odlucizarediti. Nakon što je stigao u Pariz, nastavio je svoje filozofsko obrazovanje na CollègeRoyale du France, pohadajuci paralelno i nastavu iz teologije na Sorbonni. Studije jezavršio 1611. i dobio stupanj Magister Atrium u filozofiji.

Po završetku studija, shvatio je da je spreman za miran i studiozan život jednogsamostana. Mersenne se pridružio Redu Minimis na Place Royaleu 1611. Taj red je1454. osnovao Francesco di Paola (1416-1507). Mersenne je bio posvecen pobožnostii znanosti, te je zareden za svecenika 1612. Tijekom 1614.-1618. predavao je filozofijui teologiju u samostanu u Neversu i vratio se u Pariz u manastir l’Annonciade na PlaceRoyaleu 1619., a red je podržavao njegova istraživanja.

Na pocetku je Mersenne bio pristalica skolastike, ali kasnije je postao protivnikAristotelovom ucenju (alkemija, astrologija, rosenkreutzerstvo) i postao sljedbenik mo-derne znanosti. Osim teologije, posebno je zainteresiran bio za matematiku i bio je miš-ljenja da je znanost nemoguca bez matematike. Proucavao je proste brojeve, permutacije,cikloide, barometre i zakon gravitacije, a zanimala ga je i glazba. Umro je 1648. zbogkomplikacija prouzrokovanih upalom pluca.

2.2 Razvoj znanosti u 17. stoljecu

U 16. stoljecu je veoma malen broj ljudi bio zainteresiran za znanost. Oni koji su se ba-vili znanošcu najcešce su to radili u izolaciji ili u sklopu nekog svucilišta i njihovi radoviimali su znacenja samo u lokalnim društvima. Objavljivanje radova je bilo otežano zbog

4

crkvene cenzure, a osim knjiga nije bilo drugih nacina za ucene ljude da ostanu u kon-taktu jedni sa drugima. Zahvaljujuci ocu Marinu Mersennu zabilježeni su prvi slucajeviredovitog okupljanja matematicara za koje znamo. Mersenne je bio sposoban razumijetii cijeniti rad drugih, i sam je napravio mali doprinos na putu do novih saznanja. Do-laskom u Pariz 1619. uvidio je nedostatak bilo kakve formalne organizacije u kojoj biznanstvenici mogli djelovati. Mersenne je dao sve od sebe da nešto pokrene. Njegovsamostan postao je mjesto redovitih susreta za sve one koji su htjeli razgovarati o svojimradovima i rezultatima i slušati o tudim, a on je bio veza izmedu znanstvenika iz raz-nih zemalja, posrednik znanstvenih informacija. Kada bi na nekom od okupljanja bilorezultata za predstavljanje, on bi ih tiskao na tanke listove papira, koji bi se podijelili.Potrudio se stupiti u kontakt sa svim ljudima koji su bili od neke važnosti u svijetu zna-nosti kroz mrežu dopisivanja kojom su se prenosile vijesti o napretku znanosti i novimotkricima u zamjenu za više informacija. Mersenne je poticao sve znanstvenike, koji bimogli doprinijeti pronalaženju nekog odgovora, na razmišljanje kroz brojna pitanja kojaje postavljao u svojim pismima, a on je prenosio pitanja i odgovore dalje drugima kakobi izazvao njihove reakcije.

Njegovo pisanje pisama ispunjava mnoge zadace modernog znanstvenog casopisa.Nakon njegove smrti, pisma su pronadena u njegovoj celiji i to od 78 razlicitih dopis-nika diljem Europe. Medu njima su Fermat u Francuskoj, Huygens u Nizozemskoj, Pelli Hobbes u Engleskoj te Galileo i Torricelli u Italiji. Mersenne je imao ideju postavitistupac žive na vrhu planine i promatrati ucinak atmosferskog tlaka, no propustio je pri-liku da postane slavan jer prije nego što je Mersenne uspio realizirati svoj plan, Pascalje proveo eksperiment i dokazao da visina stupca žive varira s visinom. Buduci da setalijanski slabo razumio u inozemstvu, Mersenne je imao znacajnu ulogu u popularizacijiGalileovih istraživanja diljem Europe. Vrijedno je spomenuti da je to ucinio vjerni clankatolickog reda, unatoc tadašnjem neprijateljstvu Crkve prema znanosti. Kad je cuo daGalileo piše knjigu o kretanju Zemlje, ponudio mu je pomoc s objavljivanjem knjige.Medutim, Galileo je sam bio uspješan u tome te su kopije knjige ubrzo poslane u Francu-sku. Nedugo nakon njihovog dolaska knjige su doživjele oštre kritike i osude Crkve, tesu spaljene. Mersenne je 1634. godine objavio verziju Galileovih ranih predavanja o me-hanici pod nazivom Les m’ecaniques de Galil’ee, a 1639. preveo Discorsi na francuskigodinu dana nakon objavljivanja izvornog izdanja. Nije preveo Galileov Dialogo kada sepojavio 1632. Vjerojatno zato što je osjetio da je Galileo prekršio obecanje papi da se neoslanja previše na Kopernikovu teoriju sažeto iznoseci neke njene dijelove.

Nakon Mersennove smrti, sastanci se i dalje održavaju u redovitim razmacima uraznim domovima u Parizu i okolici. Acad’emie Royale des Sciences, koja je osnovana

5

1666. smatra se izravnim nasljednikom tih brojnih privatnih okupljanja. Nova akade-mija bila je sastavljena od dva dijela: matematicki odjel koji ukljucuje sve "egzaktneznanosti" i fizicki odjel koji se bavi više "eksperimentalnim znanostima" poput fizike,kemije, botanike i anatomije. Kao što mu ime kaže, ovo udruženje je kraljevska insti-tucija, ali i znanstvena akademija. Njegovi clanovi priznaju i znanost i krunu. Državaje spremna pružiti znatna sredstva za podršku Akademije, tako da bi mogla uživati plo-dove njenih znanstvenih istraživanja. Dok se Royal Society u Engleskoj stalno bori sfinancijskim poteškocama, clanovi francuskog odjeljenja nemaju slicnih problema i dajusve svoje vrijeme za Akademiju. Sredstva iz kraljevske riznice privukla su znanstvenikeiz svih odjeljenja, tako da se s vremenom Acad’emie Royale des Sciences cini više kaoeuropsko udružnje nego francusko. Nakon nekoliko godina Acad’emie pocinje dijelitisvoje zakljucke kroz novoosnovani casopis Journal des savants. Journal des savants nijeizvorno povezan s Acad’emie. Osnovan je 1665. da bi se bavio umjetnošcu, znanosti iteologijom. Njegova pojava prouzrocila je žestoke oporbe iz vjerskih krugova tako da jeobjavljivanje privremeno bilo obustavljeno, urednik uklonjen, a tematika ogranicena prijenego što se objavljivanje nastavilo. Kad se vratio u publiciranju, postao je kvazi-službeniglasnik Acad’emie.

6

3 Mersennovi brojevi

3.1 Definicija i osnovna svojstva

Definicija 1 Mersennov broj je pozitivan prirodni broj oblika Mn = 2n− 1, gdje je nprirodan broj.

Definicija 2 Mersennov prost broj jest prost broj oblika 2p−1.

Prvih nekoliko Mersennovih brojeva su M1 = 1, M2 = 3, M3 = 7, M4 = 15, M5 =

31, M6 = 63, M7 = 127, M8 = 255 iz cega je vidljivo da su neki Mersennovi brojeviprosti, a neki složeni.

Propozicija 1 (Cataldi-Fermat) Ako je Mersennov broj Mn prost, tada je i n prost broj.

Dokaz: Ako je broj n složen, možemo ga zapisati u obliku n= rs za neke prirodne brojever, s koji su oba veci od 1. Tada je

2rs = (2s−1)(2s(r−1)+2s(r−2)+ · · ·+2s +1)

te je Mn složen jer je djeljiv s 2s−1 .

2

Primjer 1 Time smo iz Mersennovih prostih brojeva iskljucili sve Mersennove brojevesa složenim indeksom, poput

M6 = 26−1 = 63 = 7 ·9 = (23−1)(23 +1).

Stari matematicari mislili su da je Mn prost za svaki prost broj n, ali zapravo nijetako. Dokaz tome je da za proste potencije p≤ 30402457 kojih ima ukupno 1 881 339 ,Mersenovi prosti su samo za njih 43.

Primjer 2 Za p=11 imamo M11 = 211−1 = 2047 = 23 ·89 .

Za p=33 imamo M33 = 233−1 = 8589934591 = 7 ·23 ·89 ·599479 .

7

1644. godine je Mersenne u uvodu svoje knjige Cogitata physico mathematicaobjavio tvrdnju da je Mp prost za p = 2,3,5,7,13,17,19,31,67,127,257 te da je Mp

složen za sve ostale proste brojeve p < 257 . Nekoliko stotina godina nitko nije uspiopotvrditi ni opovrgnuti tu tvrdnju, iako je Mersenne napravio 5 grešaka, jer su ti brojeviveoma veliki. Americki matematicar Cole je 1903. pokazao složenost Mersennovogbroja M67.

M67 = 267−1 = 193707721 ·761838257287.

Mersenne je zabunom ukljucio M67 i M257 koji su složeni, a izostavio je M61, M89 i M107

koji su prosti.

3.2 Potraga za Mersennovim brojevima

Prva cetiri Mersennova prosta broja poznavali su još i stari Grci. To su brojevi

M2 = 3

M3 = 7

M5 = 31

M7 = 127.

Peti Mersennov prost broj, M13 = 8191, otkriven je još 1461 i ne zna se tko ga je otkrio.Sljedeca dva, M17 i M19 otkrio je Cataldi 1588., a nakon gotovo dva stoljeca Euler jepokazao da je M31 prost Mersennov broj. Iduci otkriven je bio M127 iako nije iduci povelicini, a otkrio ga je Lukas 1876. Pocetkom 20. stoljeca Powers je otkrio još dva, i toM89 1911. i M107 1914. godine.

Potraga za Mersennovim prostim brojevima znatno se ubrzala pojavom elektronic-kog racunala. Alan Turing tragao je za njima 1949. na Manchester Marku 1, ali prviuspješni pronalazak prostog Mersennovog broja nakon punih 38 godina, i to broja M521,bio je 1952. godine na racunalu SWAC na Institutu za numericke analize Sveucilišta uKaliforniji, pod vodstvom Lehmera i uz kompjuterski program za pretragu kojega je na-pisao prof. R. M. Robinson. Sljedeci, M607, pronaden je pomocu racunala samo 2 satakasnije. Sljedeca tri, M1279 , M2203 i M2281, otkriveni su tokom iducih nekoliko mjeseciistim programom. Slijede M4253, M44497, te M6972593 koji je ujedno i prvi poznati prostbroj sa preko 1000000 znamenki.

George Woltman je 1996. godine osnovao medunarodno udruženje GIMPS (GreatInternet Mersenne Prime Search) koje ima više od 100000 clanova koji tragaju za što

8

vecim Mersennovim prostim brojem. Pri tome koriste internet i zajednicko centralnoracunalo za testiranje i provjeru. Od osnivanja ovog udruženja do danas otkriveno je 13Mersennovih brojeva i svih 13 otkriveno je u okviru GIMPS projekta.

2008. godine matematicari sa UCLA koji sudjeluju u GIMPS-u osvojili su nagraduotkrivši prvi prost broj sa preko 13 milijuna znamenki, na racunalu Dell Optiplex 745.Ukupno je osam Mersennovih prostih brojeva otkriveno upravo na UCLA.

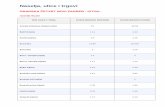
2009. otkriven je 47. po redu ali ne najveci do tada (najveci je otkriven 45. poredu) M42643801. Curtis Cooper, matematicar sa Sveucilišta Central Missouri, pronašaoje 2013. godine 48. Mersennov prosti broj, M57885161 koji je brojio 17425170 znamenki,u sklopu istraživanja koje vodi GIMPS. Dr. Cooper i njegov tim otkrili su ukupno triMersennova prosta broja prethodnih sedam godina. Na slici 1 tablicno su prikazani svido sada poznati Mersennovi brojevi.

Još nije dokazana tvrdnja da postoji beskonacno mnogo Mersennovih prostih bro-jeva.

Danas je najbolja poznata metoda za provjeru prostosti Mersennovih brojeva Lucas-Lehmerov test, koji navodimo u iducem teoremu.

Teorem 1 (Lucas - Lehmerov test) Definirajmo niz prirodnih brojeva (sn) sa s1 = 4,sn+1 = s2

n−2. Neka je p neparan prost broj. Mersennov broj Mp je prost ako i samo akoMp dijeli sp−1 za n > 1.

9

Slika 1: Otkrica Mersennovih brojeva

3.3 Neka svojstva Mersennovih brojeva

U programiranju n-bitne varijable tipa unsigned int mogu poprimiti vrijednosti od 0 doMn = 2n− 1. (n+ 1)-bitne varijable tipa signed int, koristeci metodu dvojnog komple-menta, mogu poprimiti vrijednosti cijelih brojeva izmedu −Mn i Mn−1 .Slijedi nekoliko zanimljivih teorema o Mersennovim brojevima.

Teorem 2 Ako su a i p prirodni brojevi takvi da je ap−1 prost, onda je a = 2 ili p = 1.

Dokaz:Ocito vrijedi a≡ 1 (mod a−1) . Onda je

ap ≡ 1 (mod a−1)

pa jeap−1≡ 0 (mod a−1).

To znaci da (a− 1) | (ap− 1). Medutim, ap− 1 je prost, pa je a− 1 = ap− 1 ili jea−1 =±1.

10

U prvom slucaju je a = ap, stoga je a = 0 ili a = 1 što je kontradikcija jer ni jedan odbrojeva 0 i 1 nije prost, ili je p = 1.U drugom slucaju je a = 2 ili a = 0. Ako je a = 0 onda imamo

0p−1 = 0−1 =−1,

što nije prost broj. Prema tome je a = 2.

2

Teorem 3 Ako je p neparan prost broj, onda je svaki prost broj q koji dijeli 2p−1 jednaknekom višekratniku od 2p uvecanom za 1. Ova tvrdnja vrijedi i u slucaju kada je 2p−1prost broj.

Primjer 3 25−1 = 31 je prost broj i 31 = 1+3 · (2 ·5)

211−1 = 23 ·89

gdje je 23 = 1+(2 ·11) i 89 = 1+4 · (2 ·11).

Za dokaz Teorema 3 cemo koristiti Mali Fermatov teorem.

Teorem 4 (Mali Fermatov teorem) Neka je p prost broj. Tada za svaki prirodan broj a,takav da su a i p relativno prosti, vrijedi: ap−1≡ 1 (mod p). Opcenito, za svaki prirodanbroj a vrijedi: ap ≡ a (mod p).

Dokaz Teorema 3:Prema Malom Fermatovu teoremu, q dijeli 2q−1−1.Buduci da je q djelitelj od 2p−1, za sve pozitivne cijele brojeve c, q je takoder djeliteljod 2pc−1.Kako je p prost i q nije djelitelj od 21− 1 , p je takoder najmanji pozitivni cijeli brojtakav da je q djelitelj od 2p−1.Kao posljedica toga, za sve pozitivne cijele brojeve x, q je djelitelj od 2x−1 ako i samoako je p djelitelj od x. Zato, buduci je q djelitelj od 2q−1−1 , p je djelitelj od q−1 , paje q≡ 1 (mod p) .Nadalje, kako je q djelitelj od 2p − 1, koji je neparan, q je neparan. Zato je q ≡ 1(mod 2p).

2

11

Teorem 5 Ako je p neparan prost broj, tada je svaki prost broj q koji dijeli 2p− 1 kon-gruentan ±1 modulo 8.

Dokaz :Iz uvjeta teorema direktno slijedi

2p+1 ≡ 2 (mod q),

pa je 2p+1

2 drugi korijen od 2 (mod q), tj. 2 je kvadratni ostatak modulo q. Prema kva-dratnom zakonu reciprociteta, svaki prost broj q, takav da je 2 kvadratni ostatak moduloq, je kongruentan ±1 (mod 8). Dokaz ove cinjenice je posljedica Gaussova kvadratnogzakona reciprociteta, te se može vidjeti u [5], Prop 4.1.5.

2

Teorem 6 Broj znamenki u decimalnom zapisu Mersennovog broja Mn jednak jebn · log2c+1 gdje je bxc funkcija najvece cijelo od x.

12

4 Savršeni brojevi

4.1 Definicija i osnovna svojstva

Savršeni brojevi bili su poznati Pitagori i njegovim sljedbenicima, koji su im pri-davali misticna svojstva. Pitagorejci su im dali naziv "savršeni", a podrijetlo naziva jevjerojatno religiozno ili astrološko. Filozofi su se još mnogo stoljeca kasnije bavili mis-ticnim i religijskim znacajem savršenih brojeva. Sveti Augustin objasnio je da je Bogstvorio Zemlju u tocno 6 dana kao simbol savršenog djela, a savršenstvo svemira opisanoje brojem 28, to je broj dana koliko treba da Mjesec napravi puni krug oko Zemlje.

Oko 100. godine Nikomah je u svojoj knjizi naveo prva cetiri savršena broja : 6,28, 496 i 8128. On napominje da savršeni brojevi postižu sredinu izmedu veceg i manjegzbroja pravih djelitelja, te da oni dolaze u skladnom redu. Naime 6, 28, 496, i 8128 sujedini savršeni brojevi u intervalima izmedu 1, 10, 100, 1000, 10000. Na osnovi toganastala slutnja da n-ti savršen broj ima tocno n znamenki te da parni savršeni brojevizavršavaju naizmjence na znamenke 6 i 8. Obje pretpostavke opovrgnuo je Cataldi kadaje pokazao da su da su peti, šesti i sedmi savršeni broj jednaki 33550336, 8589869056 i137438691328. Parni savršeni brojevi doista završavaju znamenkama 6 i 8, ali ne naiz-mjence.

Sa σ(n) oznacavamo sumu svih pozitivnih djelitelja prirodnog broja.

Primjer 4 Za složeni broj 15 i prosti broj 17 imamo

σ(15) = 1+3+5+15 = 24 σ(17) = 1+17 = 18.

Funkciju f : N→ C za koju vrijedi

• f (1) = 1 ,

• f (a ·b) = f (a) · f (b) za relativno proste a i b,

nazivamo multiplikativna funkcija.

Primjer 5 Pokažimo da je σ multiplikativna funkcija. Ocito je σ(1) = 1.Osim toga, σ(pk) = 1+ p+ p2 + · · ·+ pk = pk+1−1

p−1 , za prost broj p.

13

Promotrimo najprije σ(n) u slucaju n = pkql , gdje su p i q razliciti prosti brojevi. Tadaimamo:

σ(pkql) = 1+ p+ p2 + · · ·+ pk +q+ pq+ p2q · · ·+ pkq+ · · ·+ql + pql + p2ql + · · ·+ pkql

= (1+ p+ p2 + · · ·+ pk)(1+q+q2 + · · ·+ql)

=pk+1−1

p−1· q

l+1−1q−1

= σ(pk)σ(ql).

Generalizacijom prethodnog racuna dobivamo da je funkcija σ multiplikativna te

σ(pα11 pα2

2 · · · pαkk ) =

k

∏i=1

pαii −1

pi−1= σ(p1)σ(p2) · · ·σ(pk).

Definicija 3 Za prirodan broj N kažemo da je savršen ako vrijedi σ(N) = 2N .

Primjer 6 6 , 28 i 496 su savršeni brojevi.

σ(6) = 1+2+3+6 = 12 = 2 ·6

σ(28) = 1+2+4+7+14+28 = 56 = 2 ·28

σ(496) = 1+2+4+8+16+31+62+124+248+496 = 992 = 2 ·496

Definiciju 3 možemo na ekvivalentan nacin iskazati u obliku da je broj jednak sumi svo-jih pravih djelitelja. Koristimo definiciju sa funkcijom σ jer ona ima neka specificnasvojstva.

Teorem 7 Ako je n = pα11 pα2

2 · · · pαkk rastav broja n na proste faktore, onda je

σ(n) =k

∏i=1

(1+ pi + p2i + · · ·+ pαi) =

k

∏i=1

pαi+1i −1pi−1

.

Dokaz: Jedini djelitelji od pαii su 1, pi, p2

i , · · · , pαii , pa je

σ(pαii ) = 1+ pi + p2

i + · · ·+ pαii .

Prisjetimo se sume geometrijskog niza

1+ x+ x2 + · · ·+ xk =k

∑i=0

x =xk+1−1

x−1,

14

iz cega slijedi da je σ(pαii ) =

pαi+1i −1pi−1 . Buduci da je σ multiplikativna funkcija, vrijedi

σ(n) = σ(k

∏i=1

pαii ) =

k

∏i=1

σ(pαii ) =

k

∏i=1

pαi+1i −1pi−1

.

2

Lema 1 Ako η |n onda je σ(η)η≤ σ(n)

n , gdje jednakost vrijedi za η = n.

Dokaz: Ako d|n onda je n = dk, za neki k, k = nd i k|n. Ova tvrdnja vrijedi i u suprotnom

smjeru, pa imamo da d|n ako i samo ako nd |n, iz cega slijedi

σ(n) = ∑d|n

d = ∑d|n

nd= n∑

d|n

1d.

Ako je η pravi djelitelj od n, onda je

σ(n)n

= ∑d|n

1d> ∑

d′|η

1d′

=σ(η)

η

2

4.2 Parni savršeni brojevi

Pojam savršenog broja prvi je definirao Euklid u posljednjoj definiciji VII. knjigeElemenata, a u posljednjoj propoziciji IX. knjige dao je metodu kojom se može odreditisavršen broj.

Dan je geometrijski red 1 + 2 + 4 + 8 + 16 + 32 + · · · . Odredimo niz njegovihparcijalnih suma. Clanovi toga niza (sn) su 1, 3, 7, 15, 31, 63, 127, ... One clanove kojisu prosti brojevi pomnožimo sa njihovim posljednjim pribrojnikom i umnožak ce bitisavršeni broj.

Primjer 7 Prva parcijalna suma iznosi

s1 = 1+2 = 3,

a to je prost broj. Pomnožimo li ga sa posljednjim pribrojnikom te sume dobivamo 3 ·2 =

6 i broj 6 je savršeni broj.Druga parcijalna suma iznosi

s2 = 1+2+4 = 7,

15

što je takoder prost broj. Pomnožimo ga sa posljednjim pribrojnikom dobivamo 7 ·4 = 28i to je takoder savršeni broj.Treca parcijalna suma,

s3 = 1+2+4+8 = 15

nije prost broj, pa broj 15 ·8 nije savršeni broj.

Teorem 8 (Euklid) Ako je 2n−1 prost broj, onda je N = 2n−1(2n−1) savršen.

Dokaz: Ocito je da vrijedi σ(2n−1) = (1+(2n−1)) = 2n.Pa vrijedi

σ(N) = σ(2n−1)σ(2n−1) = 2n 2n−12−1

= 2n(2n−1) = 2N,

stoga je N savršen broj.

2

Traženje savršenih brojeva tako se svelo na traženje Mersennovih prostih brojeva.

Postavlja se pitanje jesu li svi savršeni brojevi Euklidovog tipa? Leonard Eulerpokazao je da je svaki paran savršen broj takvog oblika.

Teorem 9 (Euler) Ako je N paran savršen broj, onda se on može zapisati u obliku

N = 2n−1(2n−1).

Do danas nije pronaden niti jedan neparni savršeni broj, ali nije niti dokazano daoni ne postoje. Postojanje neparnih savršenih brojeva je jedan od najstarijih neriješenihproblema u matematici. Turcaninov je 1908. godine pokazao da ako postoji neparansavršeni broj, morao bi imati najmanje 5 razlicitih prostih faktora i morao bi biti veci od210. U novije vrijeme je uz pomoc suvremenih racunala pokazano da bi takav broj, kadabi postojao, morao biti veci od 10300. Danas je aktualan projekt koji se bavi proširenjemnavedene donje granice ([9]).

16

Slika 2: Graficki prikaz prvih nekoliko trokutastih brojeva

4.3 Neka svojstva parnih savršenih brojeva

Parni savršeni brojevi imaju niz svojstava. Kažemo da je broj Tn trokutast ako se grafickimože prikazati trokutastim oblikom, tj. ako je Tn = 1+2+ · · ·+n = n(n+1)

2 .

Propozicija 2 Ako je N paran savršen broj, onda je N trokutast.

Dokaz: Neka je Tk−1 trokutast broj, k prirodan broj, te

Tk−1 = 1+2+ · · ·+ k−1 =12(k−1)k.

Primjetimo da je N = 2n−1(2n−1) = 122n(2n−1).

2

Korolar 1 Ako je N savršen broj, onda je ∑d|N1d = 2

Dokaz: Pokazali smo da je d|N ekvivalentno Nd |N, stoga je

∑d|N

d = ∑d|N

Nd= N ∑

d|N

1d= 2N.

Kracenjem dobivamo ∑d|N1d = 2.

2

17

Propozicija 3 Ako je N paran savršeni broj, onda se on može zapisati kao suma odrede-nog broja kubova neparnih brojeva, tj.

N = 13 +33 + · · ·+(2n−1

2 −1)3.

Dokaz: U dokazu ce nam koristiti formulan

∑i=1

i3 =n2(n+1)2

4,

koja se lako dokazuje indukcijom po n. Uvedimo supstituciju m = 2n−1

2 .

13 +33 + · · ·+(2m−1)3 = (13 +23 + · · ·+(2m)3)− (23 +43 + · · ·+(2m)3)

=(2m)2(2m+1)2

4−23 m2(m+1)2

4= m2(2m+1)2−2m2(m+1)2

= m2(4m2 +4m+1−2m2−4m−1) = m2(2m2−1).

Kada uvrstimo m dobivamo traženi rezultat.

2

Savršeni brojevi imaju zanimljiv prikaz u binarnom zapisu. J. F. Studnicka je prvi zabi-lježio 6 = 1102, 28 = 111002, 496 = 1111100002, i 8128 = 11111110000002. Opcenito,vrijedi sljedeca propozicija:

Propozicija 4 Ako je N paran savršen broj i zapisan u binarnom brojevnom sustavu,onda on ima 2n−1 znamenki, prvih n jedinica i posljednjih n−1 nula.

Dokaz: Slijedi direktno iz binarnog zapisa brojeva, buduci da je

2p−1 = 1+2+ · · ·+2p−1.

2

Propozicija 5 Svaki parni savršeni broj završava znamenkom 6 ili 8.

Dokaz: Svaki prosti broj n veci od 2 je oblika 4m+ 1 ili 4m+ 3, za neki m. U prvomslucaju imamo

N = 2n−1(2n−1) = 24m(24m+1−1) = 16m(2 ·16m−1)

≡ 6m(2 ·6m−1)≡ 6(12−1)≡ 6 (mod 10),

18

buduci da je indukcijom po m jasno da je 6m ≡ 6 (mod 10). U drugom slucaju slicnoimamo

N = 4 ·16m(8 ·16m−1)≡ 4 ·6(8 ·6−1)

≡ 4(8−1)≡ 8 (mod 10).

Konacno, za n = 2 je N = 6 i u tom slucaju takoder tvrdnja vrijedi.

2

19

Literatura

[1] D. Burton, The history of mathematics: An introduction, Sixth edition, The Mc-GrawHill 1 Companies, New York 2007.

[2] C. von Collani, Biography of Marin Mersenne,dostupno na: http://132.187.98.10:8080/encyclopedia/en/

mersenneMarin.pdf

[3] B. Ibrahimpašic, E. Lidan, Mersennovi i savršeni brojevi, MATH-KOL (Banja Luka),2009.

[4] O. Knill, The oldest open problem in mathematics, NEU Math Circle,2007.

[5] I. Matic, Uvod u teoriju brojeva, skripta, Odjel za matematiku, Sveucilište u Osijeku,2013.

[6] J. Voight, Perfect numbers: An elementary introduction, Department of Mathema-tics, University of California, Berkeley,dostupno na: https://www.math.dartmouth.edu/~jvoight/notes/

perfelem.pdf

[7] Mersenne Primes: History, Theorems and Lists,dostupno na: http://primes.utm.edu/mersenne/

[8] Mersenne primes,dostupno na: http://en.wikipedia.org/wiki/Mersenne_prime/

[9] www.oddperfect.org

20