一、不变子空间的概念

§§7.77.7 不变子空间不变子空间

一、一、不变子空间的概念不变子空间的概念

二、线性变换在不变子空间上的限制二、线性变换在不变子空间上的限制

§7.7 §7.7 线性变换的定义线性变换的定义

三、不变子空间与线性变换的矩阵化简三、不变子空间与线性变换的矩阵化简

四、线性空间的直和分解四、线性空间的直和分解

第七章线性变换第七章线性变换


设是数域 P 上线性空间 V 的线性变换， W 是 V 的 A

的子空间，若有 ,W ( ) ( )即W W W A A

则称 W 是　的不变子空间，简称为－子空间 . A A

V 的平凡子空间（ V 及零子空间）对于 V 的任意一

个变换来说，都是－子空间 . A A

一、不变子空间一、不变子空间1 、定义

注：


1 ）两个　－子空间的交与和仍是　－子空间 .A A

2 ）设　则 W 是－子空间1 2( , , ),sW L A

1 2( ), ( ), , ( ) .s W A A A

证：显然成立 ." "

" " 任取设 ,W 1 1 2 2 ,s sk k k

则 1 1 2 2( ) ( ) ( ) ( ).s sk k k A A A A

故 W 为的不变子空间 .A

2 、不变子空间的简单性质

由于 1 2( ), ( ), , ( ) ,s W A A A ( ) .W A


1 ）线性变换的值域与核都是的A ( )VA 1 0A A

不变子空间 .

证： ( ) ( ) ,V V V A A

, ( ) ( ).V V A A A有

故　　为的不变子空间 .( )VA A

又任取有 1 0 , A 1( ) 0 (0). A A

3 、一些重要不变子空间

1(0) A 也为的不变子空间 . A


2 ）若　则与都是－子空间 . ,AB=BA ( )VB 1(0)B A

证： ( ) ( ) .V V B B

对　　　　　存在使( ), ,V V B ( ), B

于是有，

( ) ( ) ( ) ( ) ( ) ( )V A A B AB BA B A B

( )VB 为的不变子空间 . A

1 0 , 0 ,V B B其次，由

对有 1 0 , B 0. B


于是 ( ) ( ) ( ) ( ) (0) 0. B A BA AB A B A

1( ) 0 . A B

故　为　的不变子空间 . 1 0B A

的多项式的值域与核都是的不变子空间 . A ( )f A A

这里　　为中任一多项式 .( )f x [ ]P x

( ) ( )f f A A A A

注：


,W k W

4 ）线性变换的特征子空间是的不变子空间 . A0

V A , .o o oV V A有

5 ）由的特征向量生成的子空间是的不变子空间 . A A

证：设是　的分别属于特征值 1 2, , , s A

1 2, , , s 的特征向量 .

3 ）任何子空间都是数乘变换　的不变子空间 .

任取 1 2( , , , ),sL

设 1 1 2 2 ,s sk k k 则

1 1 1 2 2 2 1 2( ) ( , , , )s s s sk k k L A

1 2( , , , )sL 为的不变子空间 . A


事实上，若 , 0 .W L k k P

则为　的一组基 . L 因为 W 为－子空间，A

( ) ,W A 即必存在　使,P . A

是的特征向量 . A

特别地，由　的一个特征向量生成的子空间是一A

个一维－子空间 . A 反过来，一个一维－子空间A

必可看成是　的一个特征向量生成的子空间 . A

注：注：


二、在不变子空间二、在不变子空间 WW 引起的线性变换引起的线性变换A

定义：

不变子空间 W 上的限制 . 记作 .W

A

　在不变子空间 W 上引起的线性变换，或称作　在 AA

设　是线性空间 V 的线性变换， W 是 V 的一个　的 A A

不变子空间 . 把看作 W 上的一个线性变换，称作A


① 当时， W ( ) ( ).W A A

③ 任一线性变换　在它核上引起的线性变换是零 A

变换，即 1 00 ;

AA

即有 0

.V oEA

注：注：

当时，无意义 . W ( )W A

.W W WA②

　在特征子空间上引起的线性变换是数乘变换，0

VA


1 、设　是　维线性空间 V 的线性变换， W 是 V 的A n

－子空间，为 W 的一组基，把它扩允为1 2, , , k A

V 的一组基： 1 2 1, , , , , .k k n

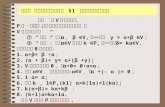
若在基下的矩阵为，则 WA 1 2, , , k

1k kA P

A在基下的矩阵具有下列形状 : 1 2, , , n

1 2

3.0

A AA

三、不变子空间与线性变换的矩阵化简三、不变子空间与线性变换的矩阵化简


反之，若 1 21 2 1 2

3, , , , , , ,0n n

A AA

A

1 .k kA P 则由生成的子空间必为的1 2, , , k A

不变子空间 .

事实上，因为 W 是 V 的不变子空间 .

1 2( ), ( ), , ( ) .k W A A A

即，均可被1 2( ), ( ), , ( )k A A A1 2, , , k

线性表出 .


从而， 1 2( , , , )n A

11 12 1 1, 1 1

11 11 2 2, 1 2

1 2 , 11 2

1, 1

, 1

( , , , )0 0 0

0 0 0

k k n

k k n

k k kk k k knn

k k kn

n k nn

a a a a aa a a a a

a a a a aa a

a a

1 21 2

3( , , , ) .0n

A AA

1 11 1 21 2 1

2 12 1 22 2 2

1 1 2 2

( )( )

( )

k k

k k

k k k kk k

a a aa a a

a a a

AA

A

设


在这组基下的矩阵为 iW

A , , 1,2, , .i in ni iA A P i s

若，则 1 2 sV W W W

1 211 1 21 2 1, , , , , , , , ,sn n s sn

为 V 的一组基，且在这组基下的矩阵为准对角阵 A

2 、设是维线性空间 V 的线性变换，都是 nAiW A

的不变子空间，而　　　　　是的一组基，且 iW1 2, , ,ii i in

1

2 .

s

AA

A

（ 1 ）


的子空间为的不变子空间，且 V 具有直和分解： AiW

1 2 .sV W W W

由此即得：

下的矩阵为准对角矩阵 (1), 则由　　　　　　生成 1 2, , ,ii i in

V 的线性变换　在某组基下的矩阵为准对角形A

V 可分解为一些　的不变子空间的直和 .A

反之，若在基 1 211 1 21 2 1, , , , , , , , ,sn n s sn A


定理 12 ：设为线性空间 V 的线性变换，是 A ( )f

1 21 2( ) ( ) ( ) ( ) srr r

sf

1 2 .sV V V V

四、线性空间的直和分解四、线性空间的直和分解

是的特征多项式 . 若具有分解式： A ( )f

再设 ( ) ( ) 0,iri iV E V A

A则　都是的不变子空间；且 V 具有直和分解：iV


证：令( )

( )( ) ii r

i

ff

( ) ,i iW f V A

则是的值域，iW ( )if A 是的不变子空间 . iW A

又 ( ) ( ) ( )i ir ri i i iE W E f V A A A

( ) ( )iri iE f V f V A A A

( ) 0.iri iE W A （ 2 ）

1 111 1 1( ) ( ) ( ) ( ) ,i i sr r rr

i i s


下证　　　　　　　　　　　分三步： 1 2 .sV V V V

1 . 证明 1 2 .sV W W W

1 2( ), ( ), ( ) 1sf f f

∴ 存在多项式使1 2( ), ( ), , ( ),su u u

1 1 2 2( ) ( ) ( ) ( ) ( ) ( ) 1s su f u f u f

于是 1 1 2 2( ) ( ) ( ) ( ) ( ) ( )s su f u f u f E A A A A A

∴ 对　有 ,V

2 . 证明　　　　　　　是直和 . 1 2 sV V V

3 . 证明 , 1,2, , .i iV W i s


1 1 2 2( ) ( ) ( ) ( ) ( ) ( ) ( )s su f u f u f A A A A A A

1 1 2 2( ) ( )( ) ( ) ( )( )f u f u A A A A

( ) ( )( )s sf u A A

这里 ( ) ( )( ) ( ) , 1,2, , .i i i if u f V W i s A A A

1 2 .sV W W W

1 1 2 2( ) ( )( ) ( ) ( )( ) ( ) ( )( )s su f u f u f A A A A A A

( )E


其中　 i iV （也即，　　　　　　　　），　　　　

( ) ( ) 0iri iE A

0, 1,2, , .i i s 则

( ) ( ),jrj if i j

∴ 存在　使 ( ),h ( ) ( )( ) .jr

i jf h

于是 ( ) ( )( ) .jr

i jf h E A A A

1 2 0s (3) 即证，若

2 . 证明　　　　　　　是直和 .1 2 sV V V


用作用（ 3 ）的两端，得 ( )if A

1 2( )( )i sf A

( )( ) ( )( ) ( )jri j j jf h E A A A

( ) ( ) 0 0, .jrj jh E h j i A A A

又 ( ),( ) 1.iri if

1 2( )( ) ( )( ) ( )( )i i i sf f f A A A

( )( ) 0i if A


( )(0) ( )(0) 0, 1,2, , .u v i s A A

( ) ( )( ) ( ) ( ) ( )iri i i iu f v E A A A A

( ) ( ) ( ) ( )( ) ( )iri i i i iE u f v E A A A A

从而 ( ) ( ) ( )( ) iri iu f v E E A A A A

所以　　　　　　　是直和 .1 2 sV V V

( ) ( ) ( )( ) 1iri iu f v

∴ 有多项式，使( ), ( )u v


3 . 证明 : ( ) ( ) 0,iri i iW V E V A

1( ) (0)ir

i iW E

A首先由 (2) ，有

1 2 , .s i iW

即 1 2 ( ) 0i s

其次，任取　　　　设,iV

.i iW V即

令 , ( ); .j j i ij i

( ) 0.iri iE W A


1 2 1 2s sV V V

0, 1,2, , .i i s

由（ 2 ） , 有　( ) ( ) 0, 1,2, , .iri iE i s A

从而有 ( ) ( ) 0, 1,2, , .iri iE i s A

( ) ( ) ( ) ( ) 0i ir ri i iE E A A

( ) ( ) ( ) ( )i ir ri i i iE E A A又

又 1 2 0,s

由，是直和，它的零向量分解式21 2 sV V V

即　　　　　　　　

,i iV

唯一 .


综合　　，即有1 ,2 ,3

1 2 .sV V V V

于是 .i iW

故 ( ) ( ) 0, .iri i iW V E V A

即有 .i iV W

是的不变子空间，且 iV A


练习：练习：设 3 维线性空间 V 的线性变换　在基A 1 2 3, ,

下的矩阵为 1 2 22 1 2 .2 2 1

A

证明：是　的不变子空间 . 1 2 1 3( , )W L A

证：令 1 1 2 2 1 3,

由 1 2 3 1 2 3( , , ) ( , , )A A

1 2 1 2 3

1 1( , ) ( , , ) 1 0 .

0 1


有

1 2 1 2 3

1 1( , ) ( , , ) 1 0

0 1

A A

1 2 3

1 1( , , ) 1 0

0 1A

1 2 3

1 2 2 1 1, , 2 1 2 1 0

2 2 1 0 1

1 2 3

1 1, , 1 0 .

0 1


即 1 1 2 1( ) A

2 1 3 2( ) A

1 2( ), ( ) .W A A

故 W 为　的不变子空间 .A

一、不变子空间的概念

Documents

Transcript of 一、不变子空间的概念

一、 不变子空间的概念

Documents

Transcript of 一、 不变子空间的概念

一、不变子空间的概念

Transcript of 一、不变子空间的概念