1  

TEMAS DE FÍSICA I LEYES DE NEWTON 

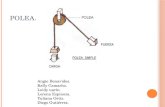
Profr. Abelardo Rodríguez Soria et al       TRIMESTRE 11‐P  Sistemas con aceleración común.  EJEMPLO 1. La máquina de Atwood.   La máquina de Atwood consiste en una polea fija en su centro (lisa y no rotatoria). Una cuerda pasa por la polea y remata en dos bloques de masas m1 y m2, como se ve en la figura 1. Se trata de calcular 

la aceleración del sistema y la tensión en la cuerda, una vez que se liberan los bloques. ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ 

 

  

   

 

Figura 1  Figura 2  Primer paso. Diagramas de cuerpo libre.   En la figura 2 se muestra el DCL de cada bloque. Advierta que existe una sola cuerda y por tanto una sola tensión, dado que la polea es lisa.  Segundo paso. Ejes de coordenadas y referencia temporal.   Se puede adoptar un sistema de ejes X, Y distinto para cada bloque. En este caso, como todas las fuerzas están verticales, solamente es necesario un solo eje para cada bloque, que designaremos “Eje X”.  

  

Figura 3  

2  xisten

os escoger arbitrariamente una de las opciones. Supondremos que m2 está acelerado 

acia ab

 para cada bloque en el sentido de su respectiva aceleración, tal como 

rcer paso. Leyes de movimiento.  a aplicar la 2a. ley de Newton a cada ue. La expresión matemática general de esta ley 

es la siguiente: 

E  aquí dos opciones de movimiento: el bloque m2 puede estar acelerado hacia abajo o hacia arriba. 

En estos casos podem

h ajo, y por tanto el bloque m1 estará acelerado hacia arriba.  

  Se recomienda trazar el Eje X envemos  la figura 3. 

  En cuanto a la referencia temporal, supondremos que t ≡ 0 cuando se liberan los bloques.  Te  Vamos  bloq

 

(i)    x x

y y

F mam F ma

ì =ï= Þ í =ïî

åå åF a  

 En el presente problema los bloques se mueven con una misma magnitud de aceleración “a”, puesto que 

extensible. Además, los vectores aceleración de cada bloque tienen solo componente X (se 

ene ax = a, ay = 0). Entonces las ecuaciones (i) se reducen para este problema a una sola, a saber, 

i)    x a

la ec  bloque: 

Bloque 1. (iii)    T – m1 g = m1 a  

 

Bloque 2. (iv)    m2 g – T = m2 a  

 

la cuerda es in

ti

 F m=å  (i

 Apliquemos  uación (ii) a cada 

  

  

Figura 4a  Figura 4b    Fíjese bien en el signo de la componente de cada fuerza. En particular, para el bloquehacia ajo son positivas, porque el eje X para este bloque está dirigido hacia abajo.  

 2 las fuerzas  ab

 T y a. 

 dinámicas.   Este paso se explicará en otro ejemplo más adelante, donde sí se necesita. 

 Cuarto paso. Incógnitas y datos.   Los datos del problema son m1, m2, y por supuesto, g. Las incógnitas son dos: Quinto paso. Relaciones cinemáticas y/o

3  

resolver ya, pues  tenemos un sistema  (iii),  (iv) de dos ecuaciones con dos cógnitas. Se recomienda “eliminar las tensiones”, lo cual podemos lograr sumando miembro a miembro 

es

– m1 g + m2 g = m1 a + m2 a 

i)   

 Sexto paso. Operaciones matemáticas.   Podemos proceder a inestas ecuacion . Obtenemos  (v)   

 de donde  

2 1(v1 2m m+

( )m m ga

-=  

 valor de a en la ecuación (iii) obtenemos   tensión: 

 

 Sustituyendo este la 

2 11 1 1 1

( )m m gT m g m a m g m

m m-

= + = + ×+

  1 2

ii)   

 o sea  

1 22m mT g

m m= ×

+ (v

1 2

 negativa. Esto significa 

 el bloque m1 hacia abajo). 

os 

bloques se moverían con velocidad constante. • Conforme se aumenta m2, manteniendo m1 constante, la aceleración tiende a la de la gravedad: 

 

 Observaciones. 

• La solución (vi) nos dice que si m1 > m2, entonces la aceleración a resultasimplemente que  los vectores aceleración mostrados en  la  figura 3  invierten  sus direcciones  (el bloque m2 estaría acelerado ahora hacia arriba,

• Por  otra  parte,  si  las masas  son  iguales  (m1  = m2),  la  aceleración  del  sistema  es  cero:  amb

 

( )121

 2 2

m2

0 0

1lim lim

1

mm

mm m

ga g

® ®

-= =

+ 

iagramas, Ejes, Leyes, Incógnitas, Relaciones, Operaciones). Este acrónimo no nción  es  servir  de  recordatorio  de  los 

distintos pasos del método.    

   y la tensión T tiende a cero.    Los pasos del método que hemos utilizado aquí para  resolver el problema  forman el  siguiente acrónimo: “D E L I R O” (Dviene  sugerido  por  experiencias  pasadas  en  el  aula ☺.  Su  inte

4  EJEMPLO  2.      EMPUJAR MEDIANTE  FUERZA NORMAL.  Se  aplica  una  fuerza  horizontal  F  a  un sistema de dos bloques en contacto que se deslizan sobre una superficie horizontal lisa, como se muestra en la figura 5.  (a) ¿Cuánto vale la aceleración de los bloques? (b) ¿Qué tipo de fuerza es la que acelera el bloque de   masa m2 y cuánto vale dicha fuerza? 

(c) ¿Qué fuerza total actúa sobre el bloque m1? 

Tome F = 40 N, m1 = 16 kg, m2 = 8 kg. 

‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐   Primer paso. Diagramas de cuerpo libre.   El  bloque  izquierdo  tiene  contacto  con  el agente que aplica la fuerza F, con el bloque derecho, y con la superficie horizontal. Estos cuerpos ejercen 

  

  

Figura 5 

sobre él las fuerzas F, la fuerza normal N y la fuerza normal N1, respectivamente. 

 

 Figura 6 

 En cuanto al bloque derecho, éste  tiene contacto con el bloque  izquierdo y con  la superficie horizontal, cuerpos que le ejercen las fuerzas N y N2, respectivamente. Los DCL’s de los bloques están en la figura 6. 

Segundo paso. Ejes y referencia temporal.   Obviamente, ambos cuerpos se van a mover con  la misma aceleración “a”, que apunta hacia  la derecha. Por tanto, escogemos los ejes X y Y para cada cuerpo como vemos en la figura 6, con el Eje X en ambos casos hacia la derecha, en el sentido de la aceleración común. Tercer Paso. Leyes de movimiento.   El movimiento de cada bloque obedece las ecuaciones   . , 0x yF ma F= =å å(La segunda se justifica por que la aceleración no posee componente Y).   He aquí las ecuaciones      Bloque izquierdo    Bloque derecho  En X:    F – N = m1  a      N = m2 a  En Y:    N1 – m1 g = 0      N2 – m2 g = 0    

5  Cuarto paso. Incógnitas y datos.   Los datos son F, m1, m2, g. Las incógnitas son N, a, N1 y N2. 

 Quinto paso. Relaciones cinemáticas y/o dinámicas.   Ambos bloques se mueven con la misma aceleración a. Ya tomamos esto en cuenta.  Sexto paso. Operaciones matemáticas.   Eliminando la normal N de las ecuaciones que contienen la aceleración a, obtenemos  

   2

48 N m216 kg 8 kg s

Fam m

= = =+ +1 2

 

   La normal N resulta igual a  

    2 2N

m8 kg 2 16N m a= = × =s

 

 (Favor de no confundir la N de fuerza normal con la N de la unidad newton). 

‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐   Otro modo de resolver este problema es el siguiente:   En primer  lugar, notemos que  ambos bloques  se mueven  juntos  con  la misma  aceleración. De hecho se comportan como si fuesen una sóla partícula de masa igual a M = 16 kg + 8 kg = 24 kg. Sobre esta partícula actúa una fuerza F = 48 N, de tal manera que la aceleración común de los bloques vale  

    248N m224kg s

Fa =M

= =  

 Figura 7 

   Apliquemos ahora  la segunda  ley “Fuerza = Masa × Aceleración” al bloque derecho. La  fuerza que lo empuja hacia la derecha es puramente la normal N. Entonces  

   2

Nm8kg 2 16N = × =s

 

 Esta  misma  fuerza  normal  N  actúa  sobre  el  bloque  izquierdo  hacia  la  izquierda.  Sumándola algebraicamente con la fuerza de 48 N sobre dicho bloque tenemos que la fuerza total sobre él es  48 N – 16 N = 32 N. Dado que la masa del bloque izquierdoes de 16 kg, su aceleración resulta de  32 N/ 16 kg = 2 m/s2, como debía.    

6  EJEMPLO 3.   JALAR MEDIANTE FRICCIÓN. Un bloque de masa m1 = 4 kg descansa sobre otro mayor 

de masa m2 = 10 kg, que puede deslizarse a  lo  largo de una mesa horizontal  lisa. Existe  fricción entre 

ambos bloques, con coeficiente de fricción estático μ = 0.5.   Se  desea  comunicar  al  conjunto  de  los  dos bloques  una  aceleración  de  a  =  0.8  m/s2,  jalando horizontalmente  con  un  cable  el  bloque  superior  con cierta  fuerza  F.  ¿Cuánto  debe  valer  esta  fuerza?  ¿Es posible esta situación?  

‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐   Discutamos  el  movimiento.  La  única  fuerza horizontal sobre el bloque inferior es la fuerza de fricción debida al bloque superior, la cual actúa hacia la derecha 

 

  

Figura 8 

sobre este bloque, impulsándolo a lo largo de la superficie horizontal. Para que ambos bloques se muevan juntos con  la misma aceleración, es menester que tal fuerza de fricción sea suficiente para producir una aceleración de 0.8 m/s2 (o sea que la fuerza de fricción logre esto sin rebasar su valor máximo permitido).   La figura 9a muestra el DCL de ambos bloques, y  las figuras 9b,c muestran respectivamente  los DCL’s del bloque superior y del bloque inferior. 

 

  

 

 

 

 

  

Figura 9a  Figura 9b  Figura 9c  

  Refiriéndonos al DCL de la figura 9a, la fuerza F necesaria para producir una aceleración común 

de 0.8 m/s2 en ambos bloques (o sea suponiendo que ambos bloques se muevan juntos como si fuesen un solo bloque de masa 14 kg) es      F = masa × aceleración = 14 × 0.8 = 11.2    (N)  Por otra parte, del DCL de la figura 9b se deduce que para que el bloque superior tenga una aceleración de 0.8 m/s2, debemos tener      F – f1 = m1 a        11.2 – f1 = 4 × 0.8    ⇒     f1 = 8 N  

¿Es esto posible? Lo será si la fricción necesaria, f1, no excede la fricción máxima fmáx permitida, la cual 

vale 

    fmáx = μ N1 = μ m1 g = 0.5 × 4 × 9.8 = 19.6  (N)  

Como  f1 = 8 < fmáx = 19.6, el movimiento conjunto de los bloques sí es posible con la aceleración dada. 

   

7  EJEMPLO 4.   Para el conjunto mostrado en la  figura,  calcular  la  aceleración  común  de los  bloques  y  las  fuerzas desconocidas. Los bloques m1  y m2  están  en  contacto  simple. 

Suponer superficies  lisas. La cuerda atada a los bloques m1 y m3 pasa por una polea lisa 

y  fija.  Suponer  que  el  bloque  m3  está 

acelerado verticalmente hacia abajo.  

 Figura 10 

Paso # 1. Diagramas de cuerpo libre de los bloques   Éstos se muestran en las figuras 11a,b,c para los bloques m1, m2 y m3, respectivamente. 

 

Figura 11a Figura 11b Figura 11c Fuerzas sobre el bloque m1, debidas a: la Tierra (W1), Cuerda (T), Bloque m2 (N2), Plano inclinado (N1). 

Fuerzas sobre el bloque m2, debidas a: la Tierra (W2), Bloque m1 (N2), Plano inclinado (N3). 

Fuerzas sobre el bloque m3 , debidas a: la Tierra (W3), Cuerda (T). 

  Advierta que  el  ángulo  θ del plano  inclinado  es  el mismo que  el que  forman  el peso W1 y  la 

normal N1 en el DCL de la figura 11a, así como el que forman W2 y N3 en el DCL de la figura 11b. 

 Paso #2. Escoger un sistema de ejes X‐Y para cada cuerpo.   Por hipótesis el bloque m3 está acelerado hacia abajo, y por  tanto  los bloques m1 y m2  lo están 

hacia arriba del plano inclinado. Esto determinará nuestra elección de ejes, como sigue:   Para los bloques m1 y m2 escogemos un Eje X a lo largo del plano inclinado, hacia arriba, y un Eje 

Y perpendicular. Para el bloque m3 es necesario sólo un Eje X, que dirigimos hacia abajo. 

  Así, para cada bloque el Eje X se dirige en el sentido de la aceleración supuesta para el mismo.  Paso #3. Plantear las ecuaciones de movimiento para cada bloque.   He aquí las ecuaciones de movimiento de los bloques: Bloque 1:    (1)  T – N2 – W1 sen θ = m1 a   (2)  N1 – W1 cos θ = 0    

8  Bloque 2:    (3)  N2 – W2 sen θ = m2 a   (4)  N3 – W2 cos θ = 0  Bloque 3:    (5)  W3 – T = m3 a  Paso #4. Incógnitas y datos.   En estas 5 ecuaciones tenemos 5 incógnitas, a saber  T, N2, a, N1, y N3. 

 Paso #5. Relaciones cinemáticas y/o dinámicas.   Ya hemos  tomado  en  cuenta  al plantear  las  ecuaciones que  todos  los bloques  tienen  la misma aceleración “a” (a1 = a2 = a3 ≡ a).  Paso #6. Operaciones matemáticas.   Para  resolver  eliminamos  la  tensión  T  de  las  ecuaciones  (1)  y  (5),  sumándolas  miembro  a miembro:  

    – N2 – m1 g sen θ + m3 g = m1 a + m3 a  

Sustituyendo aquí N2, despejada de (3) obtenemos  

    – m2 g sen θ – m2 a – m1 g sen θ + m3 g = m1 a + m3 a  

Despejando la aceleración,  

    3 1 2sen sen

(m m )sen )+ θf3 2 1m ‐m θ ‐m θa = × g (m

m +m +m1 2 3 

 

  Las demás incógnitas se calculan fácilmente a partir de “a”.  EJEMPLO 5. Una locomotora de masa 20 Mg (megagramos)  jala 4 vagones de masa 8 Mg cada uno. La 

aceleración  del  tren  en  cierto  momento  es  de  0.52  m/s2.  Calcular  en  ese  momento  la  fuerza  de acoplamiento entre la locomotora y el primer vagón y entre los demás vagones. Despreciar la fricción.  

  

Figura 12    

9    Denotemos los acoplamientos con “a”, “b”, “c” y “d”, tal como vemos en la figura 12.   Definamos un sistema que conste de los 4 vagones. Su DCL se muestra en la figura 13. 

  

Figura 13  

  La masa de este sistema es  4 × 8 Mg = 32 Mg. Dado que la única fuerza horizontal (en X) es F1, la segunda ley de Newton da  

    F1 = masa × aceleración = 32 Mg × 0.52 m/s2 = 16.64 kN  

Análogamente, el acoplamiento “b” jala los 3 últimos vagones con una fuerza F2 dada por  

    F2 = masa × aceleración = 24 Mg × 0.52 m/s2 = 12.48 kN  

El acoplamiento “c” jala los 2 últimos vagones con una fuerza F3 dada por  

    F3 = masa × aceleración = 16 Mg × 0.52 m/s2 = 8.32 kN  

Finalmente, la fuerza que jala el último vagón es      F4 = masa × aceleración = 8 Mg × 0.52 m/s2 = 4.16 kN 

   A continuación mostramos las fuerzas horizontales sobre los tres últimos vagones (figura 14a) y sobre  el penúltimo vagón  (figura 14b). En  cada  caso  se  calcula  la aceleración  (que debe dar 0.52 m/s2) usando unidades de meganewton y megagramos.  

  

a = 12.48/24 = 0.52  

 

  

a = (8.32 – 4.16)/8 = 0.52  

Figura 14a  Figura 14b  Note que  las Figs. 14a,b no  son diagramas de  cuerpo  libre, porque no muestran  todas  las  fuerzas que actúan sobre los vagones mostrados en cada caso. En ellas se muestran solamente las fuerzas horizontales.    

10  Sistemas con polea móvil y relación cinemática aB = 2 aP.   Mire los sistemas ilustrados en la figura 15.   En todos ellos existe una polea móvil (denominada “P”), sobre la que corre un cable. Uno de los extremos de este cable está fijo (el extremo “F”), y el otro extremo remata en un bloque (el extremo “B”).  

(a)  

  

(b)  

 

(c)  

  

(d)  

 

 Figura 15 

   En cada uno de estos sistemas, las aceleraciones de los bloques no son  las mismas. De hecho, el bloque B tiene el doble de aceleración que la polea móvil P, como demostraremos a continuación.   Consideremos la situación mostrada en la figura 16, que engloba todos los casos de la figura 15.  

  

Figura 16    

11    Como  la cuerda es inextensible, la suma de  las  longitudes de los tramos de cuerda a uno y otro lado de la polea móvil permanece constante. Entonces, xP + (xP – xB) = constante, o sea 2xP – xB = constante.  Derivando con respecto al tiempo tenemos 2vP – vB = 0. Volviendo a derivar,      aB = 2 aP    Esta es la relación cinemática que emplearemos en esta sección de ejemplos.  EJEMPLO  6.  Resolvamos  el  sistema  de  la  figura  17.  Existe  fricción  entre  los  bloques  y  los  planos 

inclinados, de coeficiente cinético común μc. Se desprecia la masa de la polea móvil. 

 

 

Figura 17  Hipótesis.   Polea ingrávida. Bloque m2 acelerado hacia abajo.  Diagramas de cuerpo libre. 

 Figura 18 

   Como el bloque 2 baja, las fuerzas de fricción actúan como vemos en los DCL’s de la figura 18.  Ejes de referencia.  El eje X se coloca para cada bloque en el mismo sentido que su aceleración.  Leyes de movimiento.   Las ecuaciones de movimiento de los bloques son:      Bloque 1 

(r1)    T – fc1 – m1 g sen α = m1 a1 

(r2)    N1 – m1 g cos α = 0    

12      Bloque 2 

(r3)    – 2T – fc2 + m2 g sen β = m2 a2 

(r4)    N2 – m2 g cos β = 0  Incógnitas y datos. 

  En las ecuaciones anteriores aparecen  las incógnitas T, fc1, a1, N1, fc2, a2 y N2, siete en total. Nos 

faltan 3 ecuaciones, que obtendremos en el siguiente paso.  Relaciones cinemáticas y/o dinámicas.   De acuerdo con lo discutido en la página precedente, existe la condición cinemática  (r5)    a1 = 2 a2  Además, en vista de que existe deslizamiento,  

(r6)    fc1 = μc N1 

 

(r7)    fc2 = μc N2 

 Operaciones matemáticas.   Empecemos por eliminar  la  tensión T, multiplicando  la ecuación  (r1) por 2 y sumándola con  la (r1). Luego sustituyamos las fricciones por sus expresiones dadas en (r6) y (r7). Despejemos las normales de las ecuaciones (r2) y (r4). Finalmente usemos la relación (r5). Llegaremos a  

    1 21

2 (sen cos ) (sen cos4

c cm g m ga

m m- a +m a + b - m

=+1 2

)b 

    

13  EJEMPLO 7. Un vagón de ferrocarril viaja en línea recta con aceleración constante a. Del techo del vagón cuelga una bola de masa m atada a un hilo, como vemos en la figura 19. ¿Qué ángulo θ forma el hilo con la vertical para una aceleración dada?  

  

Figura 19 ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ 

  Observe el DCL de la bola y nuestra elección de ejes en la figura 20.  

  

Figura 20  

Aplicando las ecuaciones  

    ∑Fx = max  ∑Fy = may  

y notando que las componentes de la aceleración son  ax = a  y  ay = 0, obtenemos las relaciones 

 

(r1)    T sen θ = ma        (ya que ax = a) 

(r2)    T cos θ – mg = 0       (ya que ay = 0)    Eliminemos la tensión T de las ecuaciones (r1) y (r2), dividiéndolas miembro a miembro:  

          ⇒     (r3)  a = g tan θ mgm

cosTTsen a

=θθ

   A mayor aceleración, mayor es el ángulo de  inclinación del hilo. Cuando  la aceleración tiende a infinito, dicho ángulo tiende a 90°, que correspondería a la posición horizontal del hilo.   El  conjunto  {hilo + bola}  sirve  como “acelerómetro”. Una persona que viaje en el vagón puede obtener la aceleración midiendo el ángulo θ. En particular tenemos que si el ángulo vale 45°, entonces la aceleración es  a = g. Si θ = 0, el movimiento del vagón es uniforme.     

14    CalcuT   U 

  

c

 

 

H   D

  

T sen θ = ma  ulemos la ten

 

Usando  sen2 

(r4)   

EJEMPLO 8.

cinético μc y 

Hipótesis. El sisLa ac

Diagramas dObser

y  T cos θ = msión en funcióón de la aceleeración. De las ecuaciones (r1) y (r2), o ssea mg tenemos 

T2 sen2 θ ++ T2 cos2 θ = (mma)2 + (mg)2

θ + cos2 θ = 1 hallamos 

2T m a= 2g+  

 En el sistem

entre el bloqu

ma mostrado e

ue 2 y la mesa

en la figura 21

a, de coeficien

1 existe fricci

nte cinético μión entre el bl

μc’. Calcular laloque 1 y el 2

a aceleración 

2, de coeficien

del sistema.

nte 

stema está aceceleración del

e cuerpo librerve en la figura

elerado (podrl bloque m3 es

e. a 22 el DCL de

 

Figu‐‐‐‐‐‐‐‐‐‐‐‐‐

ría estar inmóstá obviamen

e cada bloque.

Figu

ura 21 ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ 

óvil; ¿por qué?nte hacia abajo

ura 22 

 

?) o. 

15  Ejes y referencia de tiempo.  El sistema se mueve de tal manera que el bloque 3 desciende. Por lo tanto, el eje X para este bloque se escogió hacia abajo. Por otra parte, el bloque 2 se mueve hacia la derecha y el bloque 1 hacia la izquierda. En tales direcciones se toman sus respectivos ejes X. Leyes de movimiento.  Bloque 1  

(r1)    T1 – fc1 = m1 a   (r2)    N1 – m1 g = 0  Bloque 2 

(r3)    – T1 – fc1 – fc2 + T2 = m2 a 

(r4)    – N1 – m2 g + N2 = 0 

Bloque 3 

(r5)    m3 g – T2 = m3 a 

  Favor de observar que en el caso del bloque 1, que se mueve hacia  la izquierda, el eje X apunta 

hacia la izquierda por lo que T1 es positiva y fc1 negativa. Análogamente, sobre el bloque 3 el peso m3g es 

positivo y la tensión T2 negativa.  Incógnitas y datos. 

  Tenemos  7  incógnitas, T1,  fc1,  a, N1, T2,  fc2 y N2, y  5  ecuaciones. Las dos  ecuaciones  faltantes 

provienen del siguiente paso.  Relaciones cinemáticas y/o dinámicas.  En el presente problema ya hemos tomado en cuenta que todos los bloques poseen la misma aceleración “a” (o sea a1 = a2 = a3 ≡ a).   Las “relaciones dinámicas” se refieren a fuerzas. En el problema presente existen dos relaciones dinámicas, que expresan que las fricciones son las máximas, puesto que existe deslizamiento:  

(r6)    fc1 = μc N1 

 

(r7)    fc2 = μc′ N2 

 Estas dos ecuaciones complementan las 5 anteriores, por lo que ya podemos resolver.    

16   Operaciones matemáticas.  Eliminemos las tensiones, sumando miembro a miembro las ecuaciones que las contienen. Obtenemos la ecuación

(r8) – 2 fc1 – fc2 + m3 g = m1 a + m2 a + m3 a Ahora bien, las fuerzas normales son N1 = m1 g

N2 = (m1 + m2) g

y las fricciones,  

fc1 = μc N1 = μc m1 g  

fc2 = μc’ N2 = μc′ (m1 + m2) g

Sustituyéndolas en la ecuación (r8) resulta  

(r9)     c 1 c 1 2 32 m g (m m )g m gm m m

a′− μ − μ + +

=+ +1 2 3

 Ya conociendo la aceleración, las demás incógnitas se encuentran fácilmente.  Análisis de la solución.   Remitiéndonos a la figura 21: 

  Según nuestra  intuición,  si m1  es muy pesado y  el  coeficiente de  fricción  μc  (o bien  μc′) muy 

grande,  es posible que el  sistema no  se mueva.  ¿Cuál  sería  la  condición para que  el  sistema  se mueva aceleradamente? Veamos.   De (r9), la condición a > 0 equivale a la condición  

(r10)    m3 g > 2μc m1 g + μc′ (m1 + m2) g  Sin embargo, el sistema debe vencer la fricción estática para poderse mover, por lo que (r10) no es correcta, sino que debe sustituirse por esta otra:  (r11)    m3 g > 2 μ  m1 g + μ′ (m1 + m2) g  en la que figuran los coeficientes de fricción estática μ y μ′. El miembro derecho de (r11) es mayor que el correspondiente de (r10) (los coeficientes de fricción cinética son grosso modo un 25% menores que los de fricción estática). Nota.  Si  la  desigualdad  “>”  en  (r11)  se  cambia  por  una  igualdad,  el  sistema  está  en  equilibrio,  y  su movimiento es inminente.    

17  EJEMPLO 9. Un bloque tiene soldado un disco ranurado que sobresale de su cara frontal, como se ve en la figura. Se aplica una fuerza constante F en el extremo de una cuerda que pasa por la ranura del disco. La fuerza se mantiene siempre vertical. La masa del bloque junto con el disco es M. Calcular la fuerza F necesaria para producir una aceleración a hacia arriba. Suponer que no hay fricción en ninguna parte. 

Figura 23 ----------------------------

El DCL del bloque es la figura 23. Note en especial cómo actúa la cuerda sobre el disco.

Figura 23 Supondremos que el bloque está acelerado hacia arriba, por lo que dirigimos el Eje X hacia arriba. Las ecuaciones de movimiento son: En X: F – F sen θ – Mg sen θ = M a En Y: N – F cos θ – Mg cos θ = 0 La solución es

(r1) M Mg senF a + θ

=1 sen− θ

(r2) M( g) cosN a + θ

=1 sen− θ

18  (Nota. En función de la fuerza F la aceleración y la normal son:

(r3) F(1 sen ) M senga − θ − θ=

M (r4) N = (F + Mg) cos θ ) Análisis de la solución.  Cuando θ → 90° la fuerza F tiende a infinito, lo mismo que la fuerza normal N, ya que

90 90

cos senlim lim1 sen cosθ→ ° θ→ °

θ − θ⎛ ⎞⎜ ⎟

⎛ ⎞= = ∞⎜ ⎟− θ − θ⎝ ⎠ ⎝ ⎠ (Se derivó con respecto a θ el numerador y el denominador.) Se requiere cada vez mayor fuerza para acelerar al conjunto conforme el ángulo del plano es cada vez más grande. Cuando θ → 0° tenemos que F → Ma N → F + Mg como era de esperarse (Vea la figura 24).

Figura 24 De (r3) vemos que la fuerza tiene que cumplir la condición

Mg senF θ>

1 sen− θ para  que  el  bloque  esté  acelerado  hacia  arriba  (a  >  0).  Si  esta  condición  no  se  cumple,  el  bloque  está acelerado hacia abajo (a < 0).     

19  EJEMPLO 10. Un collarín de 2 kg insertado en una guía vertical lisa es jalado hacia arriba por medio de una cuerda a la que se aplica una fuerza constante de 200 N, como se muestra en la figura. Calcular la aceleración del collarín y la fuerza normal de la guía sobre él cuando la cuerda forma un ángulo de 30°.

Figura 25

La figura 26 es el DCL del collarín.

Figura 26

Plantearemos las ecuaciones de movimiento para el instante mostrado en esta figura: En X: F cos θ – N = 0 En Y: F sen θ – mg = m a La solución es N = F cos θ = 200 cos 30° = 173 (N)

00/10) sen 30° – 9.8 = 0.2 (m/s2) = (2F sen ga = θm

−

20  Problemas 1. Para el sistema mostrado, calcular las aceleraciones de los bloques y las tensiones en las cuerdas.  

 Resp. |a| = 0.143 g  2. Dos bloques están unidos por una barra de masa despreciable. Calcular  la aceleración común de  los bloques, así como la fuerza de compresión en la barra. Suponga superficies lisas.  

  

Sugerencia. Para calcular la aceleración del sistema, haga el DCL del sistema {Bloque‐1, Barra, Bloque‐2}. Después haga el DCL del sistema {Bloque‐2} para calcular la fuerza debida a la barra. Resp. a = 10 m/s2;    K = 70 N.  3. Un bloque de masa m1 = 6 kg descansa sobre otro mayor de masa m2 = 18 kg, que puede deslizarse a lo 

largo de una mesa horizontal lisa. Existe fricción entre ambos bloques, con coeficiente de fricción estático μ = 0.4. ¿Cuál es la máxima fuerza F que puede aplicarse horizontalmente sobre el bloque superior de tal modo que ambos bloques se muevan como uno sólo, con una misma aceleración? ¿Cuánto valdría esta aceleración común? ¿Qué parámetro(s) cambiaría Ud para lograr que esta aceleración fuera mayor?  

  

Resp.  F = 23.52 N;      a = 0.98 m/s2 

21  4. Un tren tiene una locomotora de 40 Mg de masa (1 megagramo = 106 g = 103 kg), que jala cuatro vagones de masas iguales de 10 Mg. Calcular las fuerzas en los acoplamientos de la locomotora con el primer vagón, y en los de vagón con vagón, suponiendo que el tren rueda con aceleración de 1 m/s2. Resp. 40, 30, 20 y 10 MN (meganewton).  5. Tres bloques, de masas 2, 8 y 5 kg, son empujados por una fuerza de 45 N, como se muestra en la figura. Intente calcular mentalmente la aceleración común del conjunto, así como las fuerzas de contacto entre los bloques. No hay fricción en ningún lado.   Resuelva de nuevo  el problema  “a pie”, haciendo  los DCL’s de  cada  bloque y  trabajando  con valores paramétricos m1, m2, m3 para las masas y para la fuerza aplicada.  

 

Resp. 3 m/s2; 39 N; 15 N.  6. Una caja de masa 50 kg es transportada en un camión. En cierto momento el camión aplica los frenos de modo que su desaceleración es constante, de magnitud 6 m/s2. El coeficiente de fricción estática entre la caja y la plataforma del camión es suficiente para que la caja no resbale.  

  

Fig. E2  ¿Qué  tipo  de  fuerza  es  la  que  desacelera  la  caja,  y  cuánto  vale?  Calcular  el  coeficiente  de  fricción suponiendo que la caja está a punto de resbalar durante el frenado.  7.  Se  comunica  al  sistema  de  dos  bloques  una  aceleración  de  2  m/s2.  ¿Cuál  es  el mínimo  valor  del coeficiente de fricción estática entre los bloques para que no haya deslizamiento del bloque superior?  

  

Note que no se requiere la masa del bloque inferior. Resp. μ = 0.2.  8. Se empuja un bloque de 35 kg con una fuerza de 150 N, como se muestra en la figura. Sobre este bloque descansa otro bloque de 15 kg. El conjunto se mueve sobre una superficie lisa, sin que el bloque de arriba se deslice. Calcular  la  fuerza de  fricción estática entre ambos bloques. ¿Puede calcular el coeficiente de fricción con estos datos? 

 

222  

R 9c

 

f R 

a 

R

 

m

R

Resp. 45 N; N

9. Una persocontacto pers“a”? Sugeren

¿Cuánto valefuerza de con

Resp. N = m (

10. Hallar  las

acelerado hac

Resp. 

11. ¿Cuál debe

misma acelera

m2 = 6 kg, F

Resp. 0.24.

o. 

ona de masa sona–elevadocia: En el DCL

e  la  fuerza P ntacto es igua

(g + a),  P = (M

s aceleracione

cia la izquierd

e ser el mínimo

ción, al bloque

= 64 N.

m  se encuenor si el elevadL del elevado

que  ejerce  el a cero? 

M + m) (g + a) 

es de  los 4 bl

da y m2 lo est

o coeficiente d

e m2? Suponga

31

mm

a =

ntra dentro dedor está aceleror no incluya 

el  cable para 

loques del sis

tá hacia la der

de fricción estát

a que la superfi

3 c 1

1 3

mg,

m ma

− μ+

e un elevadorando (a) haclas fuerzas la

  acelerar  al  co

stema mostra

recha. 

 

or de masa Mcia arriba; (b) aterales debid

tico μ para que

icie que sostien

4 c2

2

m (2m

a− μ

=+

onjunto?  ¿En

ado en  la figu

 

M.  ¿Cuánto vahacia abajo, as al cubo. 

ale  la  fuerza con aceleraci

de ión 

n qué  caso  see  tendría quee  la 

ura, suponienndo que m1 está 

2  1 2

4

m m )m

++

e el bloque m1

ne los bloques 1 pueda arrastra

es lisa. Tome mar consigo, con

m1 = 10 kg,

n la

23  12. Dos vagones con las masas indicadas se mueven hacia la derecha. Cada vagón tiene un sistema de frenos, los cuales se aplican simultáneamente, generándose una fuerza de frenado de 50 kN sobre cada vagón. ¿Cuánto vale la fuerza en el acoplamiento durante la desaceleración? ¿Es de tensión o de compresión? Repetir el problema intercambiando las masas de los vagones.

Resp. 10 kN (tensión). 10 kN (compresión). 13. Un cilindro de masa M descansa sobre dos superficies a ángulo recto como se muestra en la figura. No existe fricción en ninguna parte. ¿Para qué valor de la aceleración el cilindro está a punto de rodar hacia la izquierda?  

  Resp.  g tan θ.  14. Se aplica una fuerza constante F como se muestra en las figuras abajo. Las poleas son ideales y las superficies lisas. ¿Puede dar la aceleración del sistema en cada caso, sin necesidad de plantear las ecuaciones con detalle?

Resp. 4.2 m/s, 14 m/s.

24  15. Se aplica una  fuerza F sobre una polea  ligera y  lisa, como se muestra en  la  figura. Calcular el valor máximo de F  tal que el bloque M no se mueva, y  la aceleración consiguiente del bloque m. Tomando F igual al doble de este valor máximo calcular las aceleraciones de los bloques.  

  

Resp.  F = 2Mg,    (M m)ga −=

m 16.  Para  el  sistema mostrado  en  la  figura,  calcular  las  aceleraciones  de  los  bloques  y  la  tensión  de  la cuerda. No hay fricción entre el bloque y el plano inclinado.  

  Resp.  a = 5.9 m/s2.  17. Suponiendo que todas las superficies son lisas, que la cuerda es inextensible y que la polea es lisa y de masa insignificante, calcular la aceleración del bloque de masa M y la tensión de la cuerda.

Resp. mgM+2m

a =

25  18. Sobre el carrito actúa una fuerza que le produce una aceleración “a”. En cierto momento se rompe la cuerda. Existe fricción entre el bloque de masa m y el carrito, de coeficiente estático μ. ¿Cuál es el mínimo valor de μ tal que el bloque no caiga?  

  Resp.  g/a.  19. Calcule las aceleraciones de los bloques en el siguiente sistema. Suponga que la polea móvil no tiene masa y que no existe fricción en ninguna parte.   

  Sugerencia.  El  sistema  contiene  dos  cuerdas,  con  tensiones  que  denotamos  con  T1  y  T2. Al  aplicar  la 

segunda ley de Newton a la polea móvil tenemos que    T1 – 2 T2 = masa × aceleración = 0 

 ya que la masa es cero. Se sigue que T1 = 2 T2. Por otra parte, la aceleración de la polea móvil es la misma 

que la del bloque m1. 

 Resp. 

   2 11

2m m seng

m 4m1 2

− α+

a = ⋅

   

26  20.  En  el  sistema  mostrado,  la  polea  móvil  tiene  masa M.  Ambas  poleas  son  lisas  y  la  cuerda  es inextensible. Calcular las aceleraciones de los bloques.  

  21. En la figura, el collarín C se mueve a lo largo de la guía recta inclinada G, con aceleración constante a dirigida  como  se  muestra.  Existe  fricción  de  coeficiente  μ  entre  el  bloque  de  masa  m  y  su  apoyo horizontal, soldado al collarín. ¿Qué valor máximo puede tener la aceleración sin que el bloque se deslice? Tome el Eje X en la misma dirección que la aceleración a.  

  

Interprete la solución.  Resp. 

  θμ−θ

μ=

sencosga

 22.. Comparar las aceleraciones del bloque de masa m1 en los dos casos mostrados. 

Resp. 2 22m 2m,

4m m m 4m1 2 1 2

g ga a= =

+ +

27  23. Un bloque  acanalado de masa 8 kg  se mueve verticalmente  en una guía  lisa, mediante una  fuerza constante F aplicada como se muestra. Calcular el valor de F que  imprime una aceleración de 2 m/s2 al bloque. 

  Resp. F = 111.3 N. 24. Calcular el mínimo valor de la fuerza F tal que el bloque m no resbale hacia abajo. Calcular también la fuerza normal sobre el bloque M, debida al piso. Hay fricción entre ambos bloques, de coeficiente μ.  

 

Resp.     m(m+M)gF= , N=(m+M)gμM

 25. Resuelva el problema 12 con los bloques intercambiados (F aplicada sobre M, el bloque “m” haciendo contacto con la superficie derecha de M).  

Resp.    (m+M)gF=μ

 26. El collarín C se mueve a lo  largo de  la guía recta  inclinada G, con aceleración constante “a” dirigida como se muestra. Existe fricción de coeficiente estático μ entre el bloque de masa m y su apoyo horizontal, soldado al collarín. ¿Qué valor máximo puede tener la aceleración sin que el bloque se deslice? Compare con el resultado obtenido en el Ejercicio 12 de la página 31. ¿Puede explicar físicamente la diferencia? 

  

Resp.  a = μg /(cos θ + μ sen θ)