Recull de problemes de selectivitat sobre geometria afí i mètrica · 2019-10-14 · 2) PAU LOGSE...

Generalitat de Catalunya Departament d’Educació Institut de Gelida Departament de Matemàtiques

C/ Pasqual i Batlle, 1-15 08790 Gelida Telèfon: 93 779 04 50 e-mail: [email protected] https://agora.xtec.cat/iesgelida

RECULL DE PROBLEMES DE SELECTIVITAT SOBRE GEOMETRIA AFÍ I MÈTRICA (AMB SOLUCIÓ)

1) PAU LOGSE 1999 Sèrie 1 Problema 1: Donat el tetràedre de vèrtexs A = (0, 0, 0), B = (1, 1, 1), C = (3, 0, 0) i D = (0, 3, 0) a) Calculeu l'equació del pla que conté la cara BCD i la del pla que conté la cara ACD. b) Calculeu les equacions de dues de les altures del tetràedre, la que passa pel vèrtex A i la que passa pel vèrtex B, respectivament. (Nota: altura d'un tetràedre és la recta que passa per un vèrtex i és perpendicular al pla que determina la cara oposada.) c) Comproveu que les dues altures anteriors es tallen en un punt P. d) Comproveu si la recta que uneix qualsevol vèrtex del tetràedre amb P és perpendicular a la cara oposada (i és, per tant, una altura del tetràedre). 2) PAU LOGSE 1999 Sèrie 2 Qüestió 2:

Considereu la recta r de l'espai d'equacions 3 1

2 2

x zy

− += =

Trobeu l'equació cartesiana del pla que conté r i que passa pel punt P = (1, 1, 1) (equació cartesiana vol dir la de la forma ax + by + cz = d). 3) PAU LOGSE 1999 Sèrie 2 Problema 2: Donats els punts de l'espai A = (2, 1, 0), B = (0, 2, 0), C = (–3, 0, 0) i D = (0, –1, 0) a) Són coplanaris? Formen un paral·lelogram? b) Calculeu l'àrea del polígon ABCD. c) Calculeu el punt simètric del punt E = (1, 1, 2) respecte del pla que determinen A, B i C. d) Calculeu la distància entre la recta que passa per E i A i la recta que passa per B i C. 4) PAU LOGSE 1999 Sèrie 5 Qüestió 2:

Donades les rectes 1

4 0:

2 2 1 0

x y zr

x y z

− − = + − − =

i 2 :3

yr x z= =

Calculeu l'equació del pla paral·lel a les dues rectes que passa per l'origen. 5) PAU LOGSE 1999 Sèrie 6 Qüestió 4:

Considereu les rectes 1

: 22

xr y z

− = = − i 2 5

:2 11

x zs

x y

− = − =

:

Comproveu que aquestes dues rectes són paral·leles i calculeu l'equació del pla que les conté. 6) PAU LOGSE 2000 Sèrie 1 Problema 2:

Donats el pla π d'equació x + 2y + 3z – 1 = 0, la recta r d'equacions 2 3

4

x z

y z

= − = +

i el punt

P = (2, 1, 1), calculeu: a) Unes equacions de la recta que passa per P i és perpendicular a π . b) L'equació del pla que passa per P i és perpendicular a la recta r. c) Unes equacions de la recta que passa per P i talla perpendicularment r. d) Unes equacions de la recta que passa per P, és paral·lela al pla π i tal que el seu vector director és perpendicular al de r.



7) PAU LOGSE 2000 Sèrie 2 Problema 2:

Considereu la recta 2 5 3 0

3 2 0

x y z

x y z

− − − = − − − =

i el pla 2x – y + az + 2 = 0, on a és un paràmetre.

a) Per a quin valor de a la recta i el pla són paral·lels? Quina serà llavors la distància entre el punt P = (1, 0, –1) de la recta i el pla? b) Existeix algun valor de a per al qual la recta i el pla siguin perpendiculars? c) Determineu el valor de a perquè la recta i el pla formin un angle de 30º. 8) PAU LOGSE 2000 Sèrie 3 Problema 2: Un quadrat de l'espai té tres dels seus vèrtexs consecutius situats en els punts de coordenades enteres P = (3, –2, 4), Q = (a, –1, a + 1) i R = (2, –3, 0).

a) Tenint en compte que els vectors QP��

i QR��

han de ser perpendiculars, calculeu el valor del nombre enter a. b) Calculeu l'equació del pla que conté aquest quadrat. c) Calculeu el quart vèrtex d'aquest quadrat. d) Calculeu l'àrea d'aquest quadrat. 9) PAU LOGSE 2000 Sèrie 6 Qüestió 3:

Calculeu el peu de la recta perpendicular a la recta ( ) ( ) ( ), , 1, 1,1 0,1,1x y z λ= − + traçada des

del punt (1, 0, –1). 10) PAU LOGSE 2000 Sèrie 6 Problema 1: Considereu la recta r de l'espai que passa pel punt P = (1, 1, 3) i té per vector director

( )1 , ,1v a a= −�. Sigui π el pla que té per equació 2x + y – z = 1.

a) Determineu per a cada valor del paràmetre a la posició relativa de la recta r respecte al pla π (paral·lela, continguda o amb un punt d'intersecció). b) Hi ha alguna de les rectes r que sigui perpendicular al pla π ? c) Calculeu la distància que hi ha entre el punt P i el pla π . 11) PAU LOGSE 2001 Sèrie 2 Qüestió 3: Donats els punts de l'espai A = (2, 0, 0), B = (0, 1, 0) i C = (0, 0, 3). a) Determineu l'equació del pla π que els conté. b) Calculeu l'equació de la recta r perpendicular al pla π i que passa per l'origen. 12) PAU LOGSE 2001 Sèrie 4 Qüestió 1: Determineu per a quins valors del paràmetre a el pla π : ax + 2y + z = a és paral·lel a la recta

r : 1

1

x ay z

ax z a

− + = + = +

13) PAU LOGSE 2001 Sèrie 4 Problema 2: Sigui π el pla d'equació x – y + 2z = 3 i P el punt (1, 1, 0). a) Calculeu la distància d de P a π . b) Determineu l'equació de l'altre pla π ' paral·lel a π que també dista d del punt P. c) Determineu l'equació de la recta r perpendicular a π que passa per P.



d) Calculeu la intersecció de la recta r amb el pla π . 14) PAU LOGSE 2001 Sèrie 5 Problema 1:

Considereu a l'espai la recta r d'equacions 2 3 1

2 3 1

x y z− + += =− −

i la recta s d'equacions

4 1 4

2 3 1

x y z+ − += =−

a) Determineu el punt de tall de la recta r amb el pla z = 0. b) Comproveu que les rectes r i s són paral·leles i calculeu la distància entre elles. c) Quina és l'equació del pla que conté les dues rectes? d) Calculeu la distància del pla anterior a l'origen de coordenades. 15) PAU LOGSE 2002 Sèrie 1 Qüestió 3: Comproveu que la recta que passa pels punts A = (4, 0, 0) i B = (0, 2, 2) és paral·lela al pla d'equació x – 3y + 5z = 2, i calculeu la distància entre la recta i el pla. 16) PAU LOGSE 2002 Sèrie 1 Problema 2: Considerem el cub de vèrtexs A, B, C, D, E, F, G, H que té l'aresta de longitud 4 dm.

a) Determineu l'equació del pla inclinat EHBC si prenem com a origen de coordenades el vèrtex D i com a eixos de coordenades DA, DC i DH en aquest ordre, tenint en compte que el sentit positiu de cada un d'ells és el que sortint de l'origen D va cap a A, C i H, respectivament. b) Calculeu les equacions de les diagonals CE i AG i utilitzeu-les per calcular les coordenades del seu punt d'intersecció. 17) PAU LOGSE 2002 Sèrie 2 Qüestió 4: Calculeu l'angle que forma el pla x – 2y + z = 1 amb la recta determinada per les equacions

1

2

x t

y t

z

= = + =

18) PAU LOGSE 2002 Sèrie 2 Problema 1: Considereu les rectes r i s amb les equacions següents:

r:3 0

2 2 0

x y

x z

− + = − + =

s:13 0

2 3 0

y

x z

+ = − − =

a) Calculeu, de cada una de les rectes, un punt i un vector director. b) Determineu si existeix cada un dels objectes següents i en cas afirmatiu calculeu la seva equació:



i) El pla paral·lel a la recta s que conté la recta r. ii) El pla perpendicular a la recta s que conté la recta r. iii) La recta perpendicular a les rectes r i s que passa per (0, 0, 0).

19) PAU LOGSE 2002 Sèrie 3 Qüestió 3:

Considereu els plans d'equacions: 1 : 2 3x y zπ + − = i ( )2 : 2 2 4ax a y zπ + − + = .

a) Hi ha algun valor del paràmetre a per al qual la intersecció dels plans 1π i 2π no és una

recta? b) Calculeu un vector director de la recta que s'obté quan es fa la intersecció de 1π i 2π per al

valor del paràmetre a = 0. 20) PAU LOGSE 2002 Sèrie 3 Qüestió 4:

Considereu la recta r d'equacions: 5 7

13 4

y zx

− −− = =− −

. Calculeu els punts d'aquesta recta

situats a una distància 3 del punt A = (1, 0, 1). 21) PAU LOGSE 2003 Sèrie 2 Qüestió 3:

Considereu el punt P = (5, –2, 9) i la recta 1 1

:2 3 6

x y zr

− += =− −

.

a) Calculeu l’equació de la recta s que talla perpendicularment r i que passa per P. b) Calculeu el punt de tall Q entre les rectes r i s. 22) PAU LOGSE 2003 Sèrie 3 Qüestió 4: Considereu els punts de l’espai A = (0, –2a – 1, 4a – 2), B = (1, –3, 4), C = (3, –5, 3). a) Comproveu que el triangle de vèrtexs A, B i C és rectangle en B per a qualsevol valor de a. b) Calculeu els valors de a que fan que aquest triangle sigui isòsceles. 23) PAU LOGSE 2003 Sèrie 3 Problema 2: Un segment d’extrems A = (5, 3, 1) i B = (4, 2, –1) es divideix en tres parts iguals mitjançant dos plans perpendiculars a aquest segment. Calculeu les equacions dels dos plans i la distància entre ells. 24) PAU LOGSE 2003 Sèrie 5 Qüestió 2:

Determineu l'equació del pla que conté a la recta 1 12

yx z− = = + i passa per l'origen de

coordenades. 25) PAU LOGSE 2004 Sèrie 1 Qüestió 2: Considereu els punts de l’espai A(0, 0, 1), B(1, 1, 2) i C(0, –1, –1). a) Trobeu l’equació del pla ABC. b) Si D és el punt de coordenades (k, 0, 0), quant ha de valer k per tal que els quatre punts A, B, C i D siguin coplanaris? 26) PAU LOGSE 2004 Sèrie 3 Problema 2: Tenim quatre punts a l’espai: A(0, 0, 0); B(0, 0, 2); C(0, 2, 0) i D(2, 0, 0). Es demana:



a) representeu gràficament els quatre punts; b) calculeu el volum del tetràedre (piràmide de base triangular) ABCD; c) trobeu l’equació del pla que passa per B, C i D; d) calculeu la distància de l’origen al pla de l’apartat anterior. 27) PAU LOGSE 2004 Sèrie 4 Qüestió 1: Considereu els punts de l’espai A(1, 1, 2), B(0, 1, 1) i C(k, 1, 5). a) Trobeu l’equació de la recta que passa per A i B. b) Per a quins valors de k els punts A, B i C formen un triangle? 28) PAU LOGSE 2004 Sèrie 4 Problema 2:

Considereu la recta r d’equació

3 2

5 2

3

x t

y t

z t

= − + = − = +

i el punt M (2, 3, 7).

a) Trobeu, en funció de t, la distància de M a un punt qualsevol de la recta r. b) Trobeu les coordenades dels punts A i B de r situats a distància 3 2 del punt M. c) El triangle AMB, és rectangle en M? d) Els punts A i B formen part d’un paral·lelogram de vèrtexs ABCD que té el centre de simetria en el punt M. Calculeu les coordenades de C i D. 29) PAU LOGSE 2004 Sèrie 5 Problema 2:

Considereu les rectes 2 1

:2 1 2

x y zr

− += =− −

i

1 3

: 1 4

5

x t

s y t

z t

= + = − − = +

a) Estudieu la seva posició relativa. b) Trobeu l’equació del pla que conté s i és paral·lel a r. c) Calculeu la distància entre r i s. 30) PAU LOGSE 2005 Sèrie 1 Qüestió 3:

Trobeu la distància entre la recta 3 1 2

:4 3 3

x y zr

− − += =−

i el pla π : 3x + 4y + 7 = 0.



:2 3 3

x y zr

− − += =−

i el pla π : 2x – 3y + 3z + 5 = 0.

32) PAU LOGSE 2005 Sèrie 3 Qüestió 4: Donats els punts A = (1, 0, 0) i B (0, 0, 1):

a) Trobeu un punt C sobre la recta d’equació paramètrica

1

1

1

x

y

z

λλ

= = + = +

que faci que el triangle

ABC sigui rectangle en C. b) Trobeu l’àrea del triangle ABC. 33) PAU LOGSE 2005 Sèrie 4 Problema 2:



Una piràmide de base quadrada té el vèrtex en el pla d’equació z = 3. Tres dels vèrtexs de la base són els punts del pla OXY: A = (1, 0, 0), B = (1, 1, 0) i C = (0, 1, 0). a) Feu un gràfic dels elements del problema. Quines són les coordenades del quart vèrtex de la base, D?

b) Quin és el volum de la piràmide? 3

àrea base alturaVolum

× =

c) Si el vèrtex de la piràmide és el punt V = (a, b, 3), quina és l’equació de la recta que conté l’altura sobre la base? 34) PAU LOGSE 2006 Sèrie 1 Qüestió 1: Trobeu les coordenades dels punts situats sobre la recta d’equació (x,y,z) = (–1,1,1) + t · (1,2,1) que estan a distància 1 del pla 2x + 2y + z = 5. 35) PAU LOGSE 2006 Sèrie 1 Problema 1: Una recta r passa pel punt A = (3,0,2) i té la direcció del vector (–1,1,4). a) Trobeu quin angle forma r amb el pla horitzontal. b) Comproveu que no passa pel punt B = (1,3,10). c) Trobeu l’equació de la recta que passa per A i B. 36) PAU LOGSE 2006 Sèrie 3 Qüestió 3:

Determineu l’equació del pla perpendicular a la recta 1 0

:2 0

x yr

x z

− − = + + =

que passa pel punt

(1,1,2). Quina distància hi ha d’aquest pla a l’origen de coordenades? 37) PAU LOGSE 2006 Sèrie 3 Problema 2:


:3 2 0

x y zr

x y z

− − − = − − − =

i el pla π : 2x – y + az + 2 = 0 on a és un

paràmetre. a) Trobeu un vector director de la recta i un vector perpendicular al pla. b) Quin ha de ser el valor de a per tal que la recta i el pla siguin paral·lels? c) Esbrineu si existeixen valors de a per als quals la recta i el pla siguin perpendiculars. En cas afirmatiu, calculeu-los. d) Esbrineu si existeixen valors de a per als quals la recta i el pla formin un angle de 30º. En cas afirmatiu, calculeu-los. 38) PAU LOGSE 2006 Sèrie 4 Qüestió 3:

Calculeu l’equació de la recta paral·lela a la recta 0

:2 1

x y zr

x y z

+ − = − + =

i que passa pel punt

(0,1,0). 39) PAU LOGSE 2006 Sèrie 4 Qüestió 4: Determineu els extrems d’un segment AB sabent que el punt A pertany al pla 2 0x y z+ + = ,

el punt B pertany a la recta 1 2

2 1 3

x y z− −= =−

i el punt mitjà del segment és ( )0,0,0



40) PAU LOGSE 2007 Sèrie 1 Qüestió 2: Considereu els punts de l’espai P = (–1, a – 1, 3), Q = (0, a – 2, 1 – a) i R = (2, –1, 6 – 6a). a) Trobeu el valor de a per al qual els tres punts estan alineats. b) Quan els tres punts estan alineats, quina és l’equació de la recta que els conté? 41) PAU LOGSE 2007 Sèrie 1 Qüestió 4: Trobeu l’equació de la recta continguda en el pla : 2 6 2 0x y zπ + + − = , que talla els eixos OY i OZ. 42) PAU LOGSE 2007 Sèrie 1 Problema 1:

Considereu la recta d’equació 2 1

:2 2

y zr x

− −= = .

a) Expresseu el quadrat de la distància d’un punt qualsevol (x, y, z) de la recta al punt P = (1, 2, 5) com una funció de la coordenada x. b) Trobeu quin valor de x fa mínima aquesta funció, deduïu quin punt Q de la recta és el més proper a P i calculeu la distància del punt a la recta. c) Escriviu l’equació de la recta que passa per P i Q i comproveu que és perpendicular a r. 43) PAU LOGSE 2007 Sèrie 2 Qüestió 1:

Trobeu l’equació del pla perpendicular a la recta 1

2 3

x y z

x y

+ + = + =

que passa per l’origen de

coordenades. 44) PAU LOGSE 2007 Sèrie 2 Qüestió 4: Trobeu els punts de la recta : 1 2r x y z− = + = que equidisten dels plans

1 : 4 3 1 0x zπ − − = i 2 :3 4 1 0x yπ + − = .

45) PAU LOGSE 2007 Sèrie 2 Problema 2: A l’espai es consideren els tres plans d’equacions:

1 : 2 1x y zπ + + = 2 : 1px y pzπ + + = 3 : 2 1px y zπ + + = , on p és un paràmetre real.

a) Esbrineu per a quins valors de p els tres plans es tallen en un únic punt. Trobeu aquest punt quan p = 1. b) Hi ha algun valor de p que faci que la intersecció comuna sigui una recta? Si és així, escriviu l’equació vectorial d’aquesta recta. c) Trobeu quina és la posició relativa dels tres plans quan p = 1/2. 46) PAU LOGSE 2007 Sèrie 3 Qüestió 1: Trobeu les equacions dels plans paral·lels a : 2 2 3x y zπ − + = situats a 6 unitats de distància d’aquest. 47) PAU LOGSE 2007 Sèrie 3 Problema 1:



Una recta r és paral·lela a la recta : 1 1 1s x y z− = − = − , talla en un punt A la recta

1: 1

3 2

x yt z

− = = + , i en un punt B la recta 2 1

:2 2 3

x y zl

− −= = .

a) Trobeu l’equació del pla determinat per les rectes r i t. b) Trobeu el punt B calculant el punt d’intersecció del pla anterior amb la recta l. c) Trobeu l’equació de la recta r. d) Trobeu el punt A. 48) PAU LOGSE 2008 Sèrie 2 Qüestió 4: Trobeu l’equació de la recta perpendicular al pla : 2 3 0x y zπ − + + = , que passa pel punt

( )1,3,a− del pla.


Donades les rectes 2 1

:1 2 1

x y zr

− += =−

i 1 7 5

:1 2 3

x y zs

− + += = i el punt ( )1,1, 1P = − ,

volem trobar l’equació de la recta que passa per P i que talla r i s. Per aconseguir-ho: a) Trobeu l’equació general o cartesiana (és a dir, l’equació de la forma Ax + By + Cz + D = 0) del pla π que conté la recta r i el punt P. b) Trobeu el punt M calculant el punt d’intersecció del pla π amb la recta s. c) Trobeu l’equació de la recta que passa pels punts P i M. d) Comproveu que la recta trobada en l’apartat anterior és la que busquem. 50) PAU LOGSE 2008 Sèrie 4 Qüestió 4:

Donats el punt ( )7,5,1P = , el pla : 2 3 10x y zπ − − = i la recta 3 2 2 7

:6 2 5

x y zr

x y z

− + = − − =

:

a) Trobeu la distància del punt P al pla π . b) Trobeu la distància del punt P a la recta r. c) Trobeu la distància de la recta r al pla π . 51) PAU LOGSE 2008 Sèrie 4 Problema 2:

Les rectes 1

1:

2 1 4

x a y zr

− += = i 2

2 4:

1 2 1

x y b zr

+ − −= =−

són coplanàries (és a dir, estan

incloses en un mateix pla). a) Expliqueu, raonadament, quina és la posició relativa d’aquestes rectes. b) Trobeu la relació que hi ha entre els paràmetres a i b. c) Trobeu els valors de a i b si el pla que les conté passa pel punt P = (2, 4, 6). 52) PAU LOGSE 2008 Sèrie 5 Qüestió 4:

Donats el pla : 3 2 5 6x y zπ − + = i la recta 1 1 2

:2 1 3

x y zr

− + += =−

, busqueu el punt de tall,

si existeix.




Considereu en l’espai 3ℝ les rectes r i s, les equacions respectives de les quals són:

( ) ( ) ( ): , , 4,1,0 ,1,1r x y z mλ= + i 2 0

:1

x y mzs

x y z

+ + = + + =

en què m és un paràmetre real.

Estudieu si hi ha cap valor d’aquest paràmetre per al qual les rectes siguin perpendiculars i es tallin. 54) PAU LOGSE 2009 Sèrie 3 Qüestió 4:

Donats el pla : 2 0x y zπ + − = i el punt ( )3,2,1P =

a) Calculeu l’equació contínua de la recta r que passa per P i és perpendicular a π . b) Calculeu el punt simètric del punt P respecte del pla π . 55) PAU LOGSE 2009 Sèrie 3 Problema 2:

Siguin P = (3 – 2a, b, –4), Q = (a – 1, 2 + b, 0) i R = (3, –2, –2) tres punts de l’espai 3ℝ .

a) Calculeu el valor dels paràmetres a i b per als quals aquests tres punts estiguin alineats. b) Trobeu l’equació contínua de la recta que els conté quan estan alineats. c) Quan b = 0, trobeu els valors del paràmetre a perquè la distància entre els punts P i Q sigui la mateixa que la distància entre els punts P i R. d) Si b = 0, calculeu el valor del paràmetre a perquè els punts P, Q i R determinin un triangle equilàter. 56) PAU LOGSE 2009 Sèrie 4 Qüestió 1:

Donats el punt ( )1,2,3P = i la recta 1 2 5

:2 3 1

x y zr

− + −= =−

a) Trobeu l’equació cartesiana (és a dir, de la forma Ax + By + Cz + D = 0) del pla π que passa per P i és perpendicular a la recta r. b) Trobeu el punt de tall entre la recta r i el pla π . 57) PAU LOGSE 2009 Sèrie 4 Problema 2: Siguin r i s dues rectes de l’espai les equacions respectives de les quals, que depenen d’un

paràmetre real b, són les següents: 3 1

:2 5 1

bx y zr

x y z

+ + = + + =

, 1

:1 1 1

x y b zs

b

− + = = + −

a) Trobeu el punt de tall de la recta r amb el pla d’equació x = 0 i el punt de tall de la recta s amb aquest mateix pla. b) Calculeu un vector director per a cada una de les dues rectes. c) Estudieu la posició relativa de les dues rectes en funció del paràmetre b. 58) PAU LOGSE 2010 Sèrie 1 Qüestió 1: Trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que conté la

recta 1

1: 2

2

xr y z

− = = − i és paral·lel a la recta 2

0:

2 0

x y zr

x y z

− − = − + =

.



5 1 2:

3 2 4

x y zr

+ − −= =−

i 2

2 2 5 0:

2 11 0

x y zr

x y z

+ + + = − + + =

:



a) Comproveu que són paral·leles. b) Trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté. 60) PAU LOGSE 2010 Sèrie 2 Qüestió 2:

Donats el pla : 5 3 4x y zπ + + = i la recta 2

:2 3

ax yr

y z

− = + = −

, estudieu-ne la posició relativa

en funció del paràmetre a. 61) PAU LOGSE 2010 Sèrie 2 Qüestió 6:

Considereu la recta 4 1

: 12 1

x yr z

+ −= = −− −

.

a) Trobeu els dos punts, A i B, de la recta r que estan situats a una distància 6d = del punt P = (–1, 1, 2). b) Trobeu l’àrea del triangle de vèrtexs A, B i P. 62) PAU LOGSE 2010 Sèrie 4 Qüestió 1: Donats el pla : 2 3 4 0x y zπ + + − = i els punts P = (3, 1, –2) i Q = (0, 1, 2): a) Calculeu l’equació contínua de la recta perpendicular al pla π que passa pel punt P. b) Calculeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla perpendicular a π que passa pels punts P i Q .


Donats el punt P = (1, 0, –2) i la recta 5 3 3

:2 2 3

x y zr

− − += =−

:

a) Trobeu l’equació contínua de la recta que passa pel punt P i talla perpendicularment la recta r. b) Calculeu la distància del punt P a la recta r. 64) PAU LOGSE 2010 Sèrie 5 Qüestió 5: Siguin r i s dues rectes d’equacions

( ) ( ) ( ): , , 4,3,4 2, 1,1r x y z t= − + − i 2

: 11 3

y z as x

− −+ = =−

a) Trobeu el valor del paràmetre a perquè aquestes rectes es tallin. b) En el cas en què es tallen, trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté. 65) PAU LOGSE 2011 Sèrie 1 Qüestió 1:

Donada la recta 2 3 2

:1 0

x y zr

x z

− + = + + =

:

a) Trobeu-ne un vector director. b) Calculeu l’equació contínua de la recta paral·lela a r que passa pel punt P=(1, 0, −1). 66) PAU LOGSE 2011 Sèrie 1 Qüestió 5:



Siguin i 1

3 1: 2

2 2

y zr x

− −− = = i 2

3 1: 1

2 2

x zr y

+ += + = .

a) Comproveu que 1r i 2r són perpendiculars.

b) Comproveu que es tallen mitjançant la determinació del punt de tall. 67) PAU LOGSE 2011 Sèrie 2 Qüestió 2:

Donada la recta 2 3 2

1 0

x y z

x z

− + = + + =

, calculeu l’equació general (és a dir, de la forma Ax + By +

Cz +D= 0) del pla perpendicular a la recta que passa pel punt P = (1, 0, –1). 68) PAU LOGSE 2011 Sèrie 2 Qüestió 5:

Considereu la recta 1 2

:3 1

x yr z a

− += = −−

i el pla : 2 5 5x y zπ + − = .

a) Estudieu la posició relativa de la recta r i el pla π en funció del paràmetre a. b) Quan 3a = , calculeu la distància de la recta r al pla π . 69) PAU LOGSE 2011 Sèrie 4 Qüestió 2: Donat el pla : 2 5x y zπ + − = :

a) Calculeu l’equació del pla paral·lel al pla π que passa pel punt P=(1, 0, −1). b) Determineu també la distància entre el punt P i el pla π . 70) PAU LOGSE 2011 Sèrie 4 Qüestió 5: Calculeu l’equació general (és a dir, de la forma Ax+By+Cz+D=0) dels plans que

contenen la recta 2

:1

yr

z

= =

i que formen un angle de 45° amb el pla 0z = .

71) PAU LOGSE 2012 Sèrie 1 Qüestió 1: Donats els plans 1 :3 2 15 0x y zπ + − + = i 2 : 2 103 0x y zπ + + − = ,

a) Comproveu que són perpendiculars. b) Calculeu l’equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla perpendicular a

1π i 2π , que passa pel punt P=(1, 3, 2).


Siguin : 3 2 1x y zπ − + = i 3 1

:2 1

x yr

x y mz

+ = − + =

. Estudieu-ne la posició relativa segons

el valor del paràmetre m. 73) PAU LOGSE 2012 Sèrie 3 Qüestió 1: Digueu per a quin valor del paràmetre m els plans 1 : 1x y mzπ − + = , 2 : x y z mπ − + = i

3 : 2 3my zπ + = tenen com a intersecció una recta.



74) PAU 2012 Sèrie 3 Qüestió 3:

Donats el pla : 2 5 0x y zπ − + − = i la recta 0

:2 10

x y zr

x y z

+ + = − + =

a) Calculeu el punt d’intersecció entre el pla i la recta. b) Trobeu l’equació contínua de la recta s continguda en el pla π , que és perpendicular a la recta r i talla la recta r. 75) PAU 2012 Sèrie 3 Qüestió 6: Donats els punts P = (1, 0, 0), Q= (0, 2, 0), R = (0, 0, 3) i S = (1, 2, 3), a) Calculeu l’equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla que conté els punts P, Q i R. b) Comproveu si els quatre punts són coplanaris (és a dir, si els quatre estan continguts en un mateix pla). 76) PAU 2012 Sèrie 3 Qüestió 6: Considereu les rectes de l’espai següents:

1 1: 1

2 1

x zr y

+ −= − =−

, 4 1 2

:3 1 2

x y zs

− − −= =−

a) Comproveu que són secants. b) Calculeu l’equació contínua de la recta que les talla i que és perpendicular a totes dues. 77) PAU 2013 Sèrie 3 Qüestió 1: Sigui : 3 2 10x y zπ − + = . a) Trobeu l’equació continua de la recta r perpendicular a π que passa pel punt

( )1,3,2P = − .

b) Trobeu també l’equació cartesiana (és a dir, de la forma 0Ax By Cz D+ + + = del

pla 1π paral·lel a π que passa pel mateix punt P .


Un triangle d’àrea 3 / 2 té dos dels vèrtexs als punts ( )0,0,0P = i ( )2,0,1Q = . El

tercer vèrtex, R, és un punt de la recta 0

:1

x y zr

y

+ + = =

i té la primera coordenada

no nul·la. Calculeu les coordenades del vèrtex R. 79) PAU 2013 Sèrie 4 Qüestió 5: Donats els punts ( )1,0, 1P = − i ( )1,2,3Q = − , trobeu un punt R de la recta

3 4 3:

2 3 1

x y zr

+ + −= =−

que compleixi que el triangle de vèrtexs P , Q i R és

isòsceles, en què PR i QR són els costats iguals del triangle.



80) PAU 2013 Sèrie 5 Qüestió 1: Siguin 1π el pla 2 3 4x y z+ − = i 2π el pla 2 4 10x y z− − = .

a) Comproveu que els plans 1π i 2π són perpendiculars.

b) Trobeu l’equació continua de la recta paral·lela als plans 1π i 2π i que passa

pel que ( )1,3,2P = − .


Donats els punts ( )1, 1,2P = − , ( )2,0,1Q = i ( )3,2, 1R= − ,

a) Trobeu l’equació cartesiana (és a dir, de la forma 0Ax By Cz D+ + + = ) del pla que determinen.

b) Trobeu un punt S pertanyent a la recta 5 1 5

:2 1 3

x y zr

− − −= =− −

, de manera

que el tetraedre de vèrtexs P , Q , R i S tinguin un volum igual a 1/ 2. 82) PAU 2013 Sèrie 5 Qüestió 5:

Considereu els punts ( )1,2,4A= − i ( )3,0, 2B = − .

Trobeu l’equació del pla format per tots els punts que equidisten de A i B .

Donat un punt ( ), ,C x y z= , dividim el segment AC en tres parts iguals i obtenim els

punts ,A 1A , B i C . Trobeu el punt C .


Donats el pla : 2 3x y zπ + − = i la recta 1

:2 4

x z mr y

− += = ,

a) Comproveu que el vector característic (o normal) de π i el vector director de r són perpendiculars. b) Estudieu la posició relativa de π i r en funció del paràmetre m. 84) PAU 2013 Sèrie 1 Qüestió 5: Donats el pla : 2 3 8 0x y zπ − + − = i el punt ( )6, 3,7P = − ,

a) Trobeu l’equació contínua de la recta que passa per P i és perpendicular a π . b) Trobeu el punt del pla π que està més proper al punt P . 85) PAU 2014 Sèrie 3 Qüestió 2: Considereu el punt ( )1,2,3A = .

a) Calculeu el punt simètric del punt A respecte de la recta d’equació ( ) ( ): , , 3 , 1, 3r x y z λ λ= + − .

b) Calculeu el punt simètric del punt A respecte del pla que té per equació : 3x y zπ + + = .




Siguin r i s les rectes de 3ℝ d’equacions

2 1:

3 4

x zr y

− += = i

( ) ( ): , , 1 2 , 3 , 4 3s x y z α α α= + − + , amb α ∈ℝ .

a) Comproveu que els punts mitjans dels segments que tenen un extrem situat sobre la recta r i l’altre extrem situat sobre la recta s formen un pla. b) Trobeu l’equació general (és a dir, que té la forma Ax By Cz D+ + = ) del pla de l’apartat anterior. 87) PAU 2014 Sèrie 4 Qüestió 3: Siguin els punts ( )1,1,0P = , ( )1,0,1Q = i ( )0,1,1R = i el pla : 4x y zπ + + = .

a) Trobeu l’equació general (es a dir, que té la forma Ax By Cz D+ + = ) del pla que passa pels punts P, Q i R. b) Si S és un punt de π , comproveu que el volum del tetraedre de vèrtexs P, Q, R i S no depèn del punt S. 88) PAU 2014 Sèrie 4 Qüestió 4: Donats els plans 1 : 4 2 1x y z mπ − + = − i ( )2 : 2 2 2 2 3 1x m y z mπ − + + = + ,

a) Determineu els valors de m perquè els plans 1π i 2π s’intersequin en una recta i calculeu

un vector director de la recta resultant que no depengui de m. b) Sigui el pla : 3 2 3 8x y zπ − + = . Estudieu la posició relativa del pla π amb la recta r

definida per la intersecció dels plans 1π i 2π quan 1m= .

89) PAU 2014 Sèrie 5 Qüestió 1: Siguin r i s les rectes de 3

ℝ que tenen les equacions següents: 3

: 5 52

zr x y

−+ = − = i 3 2 1

:2 3 1

x y zs

− − += =−

a) Estudieu el paral·lelisme i la perpendicularitat entre les rectes r i s. b) Trobeu l’equació general (és a dir, que té la forma 0Ax By Cz D+ + + = ) del pla π que conté la recta r i és paral·lel a la recta s . Calculeu la distància entre la recta s i el pla π obtingut. 90) PAU 2015 Sèrie 2 Qüestió 2:

Sigui r la recta de l’espai que té per equació 1 3

:2 1

x yr z

− += =−

i sigui P el punt de

coordenades ( )6,0, 1− .

a) Trobeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla que passa

pel punt P i talla perpendicularment la recta r . b) Trobeu l’equació paramètrica del pla que passa pel punt P i conté la recta r .




Considereu a 3ℝ la recta que té per equació ( ) ( ): , , 4 2 , 2,1r x y z λ λ= − + − − i els plans 1π i

2π d’equacions 1 : 2 2 1x y zπ + + = − i 2 : 2 2 3x y zπ − + = − , respectivament.

a) Determineu la posició relativa de 1π i 2π .

b) Comproveu que tots els punts de la recta r estan situats a la mateixa distància dels plans

1π i 2π .

NOTA: Podeu calcular la distància d’un punt de coordenades ( )0 0 0, ,x y z al pla d’equació

0Ax By Cz D+ + + = amb l’expressió 0 0 0

2 2 2

Ax By Cz D

A B C

+ + +

+ +


Siguin el punt ( )2,0,2P = i el pla π d’equació 1x y z− + = .

a) Calculeu l’equació paramètrica de la recta que passa pel punt P i és perpendicular al pla π. b) Calculeu la distància del punt P al pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Siguin a 3ℝ el punt ( )2,3,3P = i la recta ( ) ( ) ( ): , , 1,2,3 1,1,1r x y z t= + .

a) Calculeu l’equació paramètrica del pla que passa pel punt P i conté la recta r . b) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla que

passa pel punt P i és perpendicular a la recta r . 94) PAU 2015 Sèrie 5 Qüestió 2:

A l’espai tridimensional considereu la recta ( ) ( ): , , 3 2 , ,3r x y z α α α= + − − i els plans

1 : 1x y zπ + + = − i ( ) ( )2 : , , 2 ,1 ,x y zπ λ λ µ µ= + − + .

a) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla 2π .

b) Trobeu els dos punts de la recta r que equidisten dels plans 1π i 2π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Siguin els plans de 3ℝ 1 : 2y zπ − + = , 2 : 2 1x y zπ − + + = i 3 : 2 2 1x zπ − = − .



a) Calculeu la posició relativa dels tres plans. b) Comproveu que el pla 3π és paral·lel a la recta definida per la intersecció dels plans 1π i

2π .

96) PAU 2016 Sèrie 1 Qüestió 1: Siguin la recta r: (x, y, z) = (5 + k, k, –2 – 2k) i els punts P = (1, 0, –1) i Q = (2, 1, 1). a) Calculeu l’equació paramètrica de la recta que passa pel punt Q i és perpendicular al pla determinat per la recta r i el punt P. b) Calculeu el punt de la recta r que equidista dels punts P i Q. 97) PAU 2016 Sèrie 1 Qüestió 6: Responeu a les qüestions següents: a) Calculeu l’equació cartesiana (és a dir, que té la forma Ax + By + Cz = D) del pla que passa pel punt de coordenades (0, 0, 1) i és perpendicular als plans 3x + y – z = 1 i x + y + 2z = 5. b) Suposeu que un pla 1π és perpendicular a un segon pla 2π i que el pla 2π és a la vegada

perpendicular a un tercer pla 3π . Expliqueu raonadament si necessàriament els plans 1π i 3π

han de ser perpendiculars entre ells. 98) PAU 2016 Sèrie 3 Qüestió 2:

A 3ℝ , siguin la recta r que té per equació ( ) ( ), , 1 , , 1x y z λ λ λ= + − i el pla π d’equació

2 2x y z− + = − . a) Determineu la posició relativa de la recta r i el pla π . b) Calculeu la distància entre la recta r i el pla π .

Nota: Podeu calcular la distància d’un punt de coordenades ( )0 0 0, ,x y z al pla d’equació


2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Siguin a 3ℝ el pla π d’equació 2 2x y z− + = i els punts ( )3, 1,2A= − i ( )1,1, 2B = − .

a) Comproveu que els punts A i B són simètrics respecte del pla π . b) Si r és la recta dels punts P que té per equació P B vλ= + , en què λ és un paràmetre

real i ( )1,1,0v = , verifiqueu que els punts mitjans dels segments AP pertanyen al pla π .


Siguin les rectes ( ) ( ) ( ): , , 2,3, 3 1, 1,0r x y z λ= − + − i 3

: 5 22

xs y z

− = − = + .

a) Estudieu si les rectes r i s són paral·leles o perpendiculars. b) Determineu la posició relativa de les rectes r i s i calculeu l’equació paramètrica de la recta t que talla perpendicularment la recta r i la recta s. 101) PAU 2017 Sèrie 1 Qüestió 2:



a) Considereu els plans 1 :5 7 1x y zπ − − = i 2 : 2 3 5x y zπ + + = .

Determineu l’equació general (és a dir, la que té la forma Ax By Cz D+ + = ) del pla que

passa per l’origen de coordenades i és perpendicular als plans 1π i 2π .

b) Calculeu l’angle que formen els plans 1π i 2π .


Considereu el pla : 1x y zπ + + = i la recta r que passa pels punts ( )0,0,6P = i

( )1,2,3Q =

a) Estudieu la posició relativa de la recta r i el pla π . b) Calculeu la distància entre la recta r i el pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


A 3ℝ , siguin la recta 2

:2 4

x zr

y z

− = + =

i el punt ( )0,1, 1P = − .

a) Calculeu l’equació general (és a dir, la que té la forma Ax By Cz D+ + = ) del pla π

perpendicular a la recta r i que passa pel punt P . b) Calculeu el punt simètric del punt P respecte del pla 3x y z+ + = − . 104) PAU 2018 Sèrie 1 Qüestió 2:

Sigui r la recta que passa pels punts ( )0,1,1A = i ( )1,1, 1B = − .

a) Trobeu l’equació paramètrica de la recta r . b) Calculeu tots els punts de la recta r que estan a la mateixa distància dels plans

1 : 2x yπ + = − i 2 : 1x zπ − = .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Considereu els punts ( )3, 2,1P = − , ( )5,0,3Q = , ( )1,2,3R = i la recta 1 0

:2 3 5 0

x yr

y z

+ + = + − =

a) Determineu l’equació general (és a dir, que té la forma Ax By Cz D+ + = del pla que

passa per P i Q i és paral·lel a la recta r .

b) Donats el pla 2 7x y mz+ + = i el pla que passa per P , Q i R , trobeu m perquè siguin paral·lels i no coincidents. 106) PAU 2018 Sèrie 3 Qüestió 3:



Considereu el pla que té com a vectors directors ( )1,3,2u = − i ( )2,1,0v = i que passa pel

punt ( )1,0,3A = .

a) Calculeu l’equació de la recta que és perpendicular al pla i passa pel punt A.

b) Calculeu la distància del punt ( )1,5,0P = al pla.



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Considereu els punts de l’espai tridimensional ( )1,1,0A = , ( )3,5,0B = i ( )1,0,0C = i la

recta : 12

zr x y= − = .

a) Trobeu el punt d’intersecció de la recta r amb el pla que passa pels punts A, B i C . b) Trobeu els punts P de la recta r per als quals el tetraedre de vèrtexs P, A, B i C té un

volum de 32u . NOTA: El volum d’un tetraedre de vèrtexs P , Q , R i S es pot calcular amb l’expressió

( )1det , ,

6PQ PR PS��

.


Siguin el pla d’equació : 0x y zπ + − = i el punt ( )2,3,2P = .

a) Calculeu el punt simètric del punt P respecte del pla π . b) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = ) dels dos plans

paral·lels a π que estan a una distància 3 del punt P.



2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Siguin les rectes 1

2: 1 5

1

yr x z

−− = = −−

i ( ) ( )2 : , , 2 3 , 1 ,2r x y z λ λ= − − + .

a) Trobeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = ) del pla que conté

la recta 1r i és paral·lel a la recta 2r .

b) Digueu quina condició s’ha de complir perquè existeixi un pla que contingui la recta 1r i sigui

perpendicular a la recta 2r . Amb les rectes 1r i 2r de l’enunciat, comproveu si existeix un pla

que contingui la recta 1r i sigui perpendicular a la recta 2r .




Un dron es troba en el punt ( )2, 3,1P = − i volem dirigir-lo en línia recta fins al punt més

proper del pla d’equació : 3 4 15 0x zπ + + = . a) Calculeu l’equació de la recta, en forma paramètrica, que ha de seguir el dron. Quina distància ha de recórrer fins a arribar al pla? b) Trobeu les coordenades del punt del pla on arribarà el dron.

NOTA: Podeu calcular la distància que hi ha d’un punt de coordenades ( )0 0 0, ,x y z al pla

d’equació 0Ax By Cz D+ + + = amb l’expressió 0 0 0

2 2 2

Ax By Cz D

A B C

+ + +

+ +.


Siguin la recta 2

:1

xr

y z

= − =

i el pla : 3x zπ − = .

a) Calculeu l’equació paramètrica de la recta que és perpendicular al pla π i que el talla en el mateix punt en què el talla la recta r.

b) Trobeu els punts de r que estan a una distància de 8 unitats del pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

112) PAU 2019 Sèrie 4 Qüestió 5: Considereu els plans 1 : 2 5x ay zπ + + = , 2 : 1x ay zπ + + = i

( ) ( )3 : 2 1 1 0x a y a zπ + + + + = , en què a és un paràmetre real.

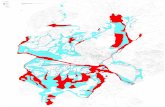
a) Estudieu per a quins valors del paràmetre a els tres plans es tallen en un punt. b) Comproveu que per al cas 1a = la interpretació geomètrica del sistema format per les equacions dels tres plans és la que es mostra en la imatge següent:



SOLUCIONARI: 1) PAU LOGSE 1999 Sèrie 1 Problema 1: Donat el tetràedre de vèrtexs A = (0, 0, 0), B = (1, 1, 1), C = (3, 0, 0) i D = (0, 3, 0) a) Calculeu l'equació del pla que conté la cara BCD i la del pla que conté la cara ACD.

• Equació del pla que conté la cara BCD:

( ) ( ) ( )3,0,0 1,1,1 2, 1, 1BC C B= − = − = − −��

( ) ( ) ( )0,3,0 1,1,1 1,2, 1BD D B= − = − = − −��

Equació del pla que passa pel punt B amb vectors directors BC��

i BD��

:

1

1 2 1

: 1 1 2 0 3 0

1 1 1

x

y x y z

z

π− −− − = → + + − =− − −

(Equació del pla que conté la cara BCD)

• Equació del pla que conté la cara ACD:

( ) ( ) ( )3,0,0 0,0,0 3,0,0AC C A= − = − =��

( ) ( ) ( )0,3,0 0,0,0 0,3,0AD D A= − = − =��

Equació del pla que passa pel punt A amb vectors directors AC��

i AD��

:

2

0 3 0 3 0

: 0 0 3 0 0 3 0 9 0 0

0 0 0 0 0

x x

y y z z

z z

π−− = → = → = → =−

(Equació del pla que conté la

cara ACD) b) Calculeu les equacions de dues de les altures del tetràedre, la que passa pel vèrtex A i la que passa pel vèrtex B, respectivament. (Nota: altura d'un tetràedre és la recta que passa per un vèrtex i és perpendicular al pla que determina la cara oposada.)

• Equació de l’altura que passa per A: Aquesta altura serà la recta 1r que passa per A i és perpendicular a la cara del tetraedre

que formen els tres vèrtexs que no són A, és a dir, la recta 1r que passa per A i és

perpendicular a la cara BCD. Per tant, la recta 1r que passa per A i és perpendicular al pla

1 : 3 0x y zπ + + − = .

1r perpendicular a ( )1 1 11 1,1,1r rv n vππ → = → =� � �

Per tant, 1r passa pel punt ( )0,0,0A= i té com a vector director ( )1

1,1,1rv =� :

1 1 1

0 0 0: : :

1 1 1

x yx y zr r x y z r

x z

=− − −= = → = = → =

• Equació de l’altura que passa per B:



Aquesta altura serà la recta 2r que passa per B i és perpendicular a la cara del tetraedre

que formen els tres vèrtexs que no són B, és a dir, la recta 2r que passa per B i és

perpendicular a la cara ACD. Per tant, la recta 2r que passa per B i és perpendicular al pla

2 : 0zπ = .

2r perpendicular a ( )2 2 22 0,0,1r rv n vππ → = → =� � �

Per tant, 2r passa pel punt ( )1,1,1B = i té com a vector director ( )2

0,0,1rv =� :

( ) ( )( ) ( )2 2

1 1 0 1 1 0 11 1 1: :

1 0 10 0 1 1 1 0 1

x z x xx y zr r

y yy z

⋅ − = ⋅ − − = = − − − = = → → → − = =⋅ − = ⋅ −

c) Comproveu que les dues altures anteriors es tallen en un punt P.

Tenim que 1 :x y

rx z

= =

i 2

1:

1

xr

y

= =

. Tenim el sistema:

( ) ( )

1

1, , 1,1,1

1 1

1 1

x y y

x z zx y z

x x

y y

= = = = → → = = = = =

( )1,1,1P→ =

d) Comproveu si la recta que uneix qualsevol vèrtex del tetràedre amb P és perpendicular a la cara oposada (i és, per tant, una altura del tetràedre).

• Comprovem que la recta que uneix el vèrtex A amb P és perpendicular a la cara BCD: Això és el mateix que comprovar que la recta 1r trobada en l’apartat b) que per construcció

uneix A amb P és perpendicular a la cara BCD. Però aquesta recta sí que és perpendicular a la cara BCD per construcció. (Era l’altura que passava per A) • Anàlogament la recta que uneix el vèrtex B amb P també és perpendicular a la cara ACD. • Resta per comprovar que la recta que passa per C i P és perpendicular a la cara ABD i que la recta que passa per D i P és perpendicular a la cara ABC. Comprovem la 1a: Per comprovar que la recta que passa C i P és perpendicular a la cara ABD solament cal

comprovar que el vector director d’aquesta recta CP��

és perpendicular als vectors AB��

i

AD��

. Tenim que:

( ) ( ) ( )1,1,1 3,0,0 2,1,1CP P C= − = − = −��

( ) ( ) ( )1,1,1 0,0,0 1,1,1AB B A= − = − =��

( ) ( ) ( )0,3,0 0,0,0 0,3,0AD D A= − = − =��

Ara tenim dos possibilitats, comprovar que els productes escalars CP AB⋅��

i CP AD⋅��

són

tots dos zero o també que el vector CP��

és proporcional al producte vectorial AB AD×��

. Anem a fer-ho mitjançant el producte escalar:

( ) ( )2,1,1 1,1,1 2 1 1 0CP AB⋅ = − ⋅ = − + + =��



( ) ( )2,1,1 0,3,0 0 3 0 3 0CP AD⋅ = − ⋅ = + + = ≠��

Per tant, la recta que passa per C i per D no és perpendicular a la cara ABD i podem assegurar que en general no existeix cap punt on es troben totes les altures d’un tetraedre.


Considereu la recta r de l'espai d'equacions 3 1

2 2

x zy

− += =

Trobeu l'equació cartesiana del pla que conté r i que passa pel punt P = (1, 1, 1) (equació cartesiana vol dir la de la forma ax + by + cz = d).

( )3,0, 1A= − és un punt de la recta r i ( )2,1,2u =� és el seu vector director.

( ) ( ) ( )1,1,1 3,0, 1 2,1,2AP P A= − = − − = −��

.

El pla π que busquem serà el pla que passa pel punt ( )1,1,1P = i té com a vectors

directors ( )2,1,2u =� i ( )2,1,2AP= −��

. Per tant:

1 2 2

: 1 1 1 0 : 2 1

1 2 2

x

y y z

z

π π− −− = → − =−

3) PAU LOGSE 1999 Sèrie 2 Problema 2: Donats els punts de l'espai A = (2, 1, 0), B = (0, 2, 0), C = (–3, 0, 0) i D = (0, –1, 0) a) Són coplanaris?

A, B, C i D coplanaris sii ho són els vectors AB��

, AC��

i AD��

.

( ) ( ) ( )0,2,0 2,1,0 2,1,0AB B A= − = − = −��

( ) ( ) ( )3,0,0 2,1,0 5, 1,0AC C A= − = − − = − −��

( ) ( ) ( )0, 1,0 2,1,0 2, 2,0AD D A= − = − − = − −��

2 5 2

, , 1 1 2 0

0 0 0

AB AC AD

− − − = − − = →

�� Coplanaris

Formen un paral·lelogram?

Un paral·lelogram és un quadrilàter de costats paral·lels dos a dos. Per tant hem de comprovar si els vectors són paral·lels dos a dos.

( ) ( ) ( )0,2,0 2,1,0 2,1,0AB B A= − = − = −��

( ) ( ) ( )3,0,0 0,2,0 3, 2,0BC C B= − = − − = − −��

( ) ( ) ( )0, 1,0 3,0,0 3, 1,0CD D C= − = − − − = −��

( ) ( ) ( )0, 1,0 2,1,0 2, 2,0AD D A= − = − − = − −��



Es veu clarament que no hi ha parells de vectors proporcionals i per tant el quadrilàter no és un paral·lelogram.

b) Calculeu l'àrea del polígon ABCD.

En l’apartat A hem comprovat que els punts A, B, C i D són coplanaris, però si ens fixem això era obvi donat que tots 4 tenen la tercera component igual a 0. Per tant, aquestos punts no solament són coplanaris sinó que tots 4 estan en el pla 0z = . Per tant, si ens

dibuixem les altres dos components, és a dir, ( )2,1A= , ( )0,2B = , ( )3,0C = − i

( )0, 1D = − tenim el següent esquema:

Podem dividir el polígon amb dos triangles BDA i BDC. El triangle BDA té la base BD de longitud igual a 3 unitats i l’altura relativa a aquesta base de longitud 2. Per tant, la seva àrea és de 3. El triangle BDC té la base BD de 3 unitats i l’altura relativa a aquesta base també de 3 unitats, per tant, la seva àrea és de 9

2 unitats.

Sumant: 9 6 9 152 2 2 23+ = + =

c) Calculeu el punt simètric del punt E = (1, 1, 2) respecte del pla que determinen A, B i C.

Podem calcular-lo però el pla que determinen els punts A, B i C és el pla : 0zπ = . Per

tant, calcularem el simètric del punt E respecte d’aquest pla. Per fer-ho calculem la recta r que passa per E i és perpendicular al pla : 0zπ = .

rr vπ⊥ → � proporcional a rn vπ →��

proporcional a ( )0,0,1 .

Així ( ) ( ) ( ) 1 1 2: , , 1,1,2 0,0,1

0 0 1

x y zr x y z λ − − −= + → = = →

( ) ( )( ) ( )

1 1 0 2 1 0 1:

1 0 11 1 0 2

x z x xr

y yy z

⋅ − = ⋅ − − = = → → → − = =⋅ − = ⋅ −

Ara fem el punt de tall de la recta r amb el pla π obtenint el següent sistema:

0

1

1

z

x

y

= = =

que òbviament té la solució ( )1,1,0P =

( ) ( ) ( )1,1,0 1,1,2 0,0, 2EP P E= − = − = −��

La solució al nostre problema serà el punt:

( ) ( ) ( )1,1,0 0,0, 2 1,1, 2Q P EP= + = + − = −��

d) Calculeu la distància entre la recta que passa per E i A i la recta que passa per B i C. • Primer que res hem de calcular les equacions d’aquestes rectes i determinar la seva posició relativa.



• Recta r que passa pels punts E = (1, 1, 2) i A = (2, 1, 0):

( ) ( ) ( )2,1,0 1,1,2 1,0, 2EA A E= − = − = −��

, aleshores:

( )0 1 11 1 2

:2 1 2 2 41 0 2

y yx y zr

x z x z

= − =− − − = = → ≅ − − = − + =−

• Recta s que passa pels punts B = (0, 2, 0) i C = (–3, 0, 0):

( ) ( ) ( ) ( )3,0,0 0,2,0 3, 2,0 3,2,0sBC C B v= − = − − = − − → =��

, aleshores:

( )2 3 3 03:

2 3 63 2 0 0 3

x y zx y zs

x yz

+ = =+ = = → ≅ − = −=

• Posició relativa de r i s: Donat que el sistema que surt és molt fàcil el resoldrem directament:

32

11 1

02 4 0

20 2 4

2 3 6 2 3 6

yy y

zx z z

xz x

xx y x −

== = =+ = = ≅ ≅ → == =

=− = − − = −

Sistema incompatible, i com les dues rectes r

i s no són paral·leles perquè els seus vectors directors no són proporcionals podem afirmar que r i s es creuen. Utilitzant la fórmula per la distància entre dues rectes que es creuen tenim que:

( ) ( ) ( ) ( ) ( )22 2

2 1 3

1 0 2, , 0 2 0 14 14

,1,0, 2 3,2,0 4, 6,2 4 6 2

r s

r s

AB v vd r s

v v

−

− −= = = = =

× − × − + − +

��

� �

14 14

256= =



4 0:

2 2 1 0

x y zr

x y z

− − = + − − =

i 2 :3

yr x z= =

Calculeu l'equació del pla paral·lel a les dues rectes que passa per l'origen.

Si un pla π és paral·lel a una recta r aleshores el vector director de la recta, també ho

serà del pla. Per tant, els dos vectors directors d’aquestes rectes 1v�

i 2v�

seran vectors

directors del pla π que finalment quedarà completament determinant afegint que passa

per l’origen de coordenades ( )0,0,0O = .

Per tant, calculem els vectors directors de les rectes:

1

4 0 4 4:

2 2 1 0 2 2 1 2 2 1zx y z x y z x y

rx y z x y z x y

λ λλ

=− − = − = − = → → + − − = + = + + = +

Sumant les equacions tenim que: 1

6 3 12 6

x xλλ= + → = +



1 24 4 4

2 6 3x y y x

λλ λ λ λ − = → = − = + − = +

Així: ( ) ( )1

1 2 1 2 1, , , , : , , , ,0 ,1,1

2 6 3 6 3 2x y z r x y z

λ λ λ λ = + + → = + →

( ) ( ) ( )1 1

1 2: , , , ,0 1,2,2 1,2,2

6 3r x y z vλ → = + → =

�

( )2 1,3,1v =�

Per tant π serà el pla que passa pel punt ( )0,0,0O = i té com a vectors directors

( )1 1,2,2v =� i ( )2 1,3,1v =� . És a dir:

0 1 1 1 1

: 0 2 3 0 2 3 0 : 4 0

0 2 1 2 1

x x

y y x y z

z z

π π−− = → = → − − =−


Considereu les rectes 1

: 22

xr y z

− = = − i 2 5

:2 11

x zs

x y

− = − =

:

Comproveu que aquestes dues rectes són paral·leles i calculeu l'equació del pla que les conté. Per comprovar que les dues rectes són paral·leles podem veure que els seus vectors directors són proporcionals o treballar per rangs. Com desprès hem de calcular el pla que conté les dues rectes, necessitarem un punt de cada recta i el vector director. Així que deixarem de banda els rangs i treballarem per vectors.

( ) ( ) ( )1: 2 : , , 1,0,2 2,1,1

2

xr y z r x y z λ− = = − → = +

2 5 2 5 2 5:

2 11 2 11 2 11zx z x z x

sx y x y x y

λ λ=− = = + = + ≅ → − = − = − = Restant les equacions:

2 2 6 3y yλ λ→ = − → = − Així:

( ) ( ) ( ) ( ) ( ), , 2 5, 3, : , , 5, 3,0 2,1,1x y z s x y zλ λ λ λ= + − → = − +

Podem observar que r sv v= →� �

r i s paral·leles o coincidents.

( )1,0,2A r= ∈ i

( )5, 3,0B s= − ∈

( ) ( ) ( )5, 3,0 1,0,2 4, 3, 2AB B A= − = − − = − −��

que no és proporcional a rv

�, per tant: r i s paral·leles:

Per calcular el pla π que conté les dues rectes farem el pla que conté els vectors ( )2,1,1rv =�

( )4, 3, 2AB= − −��

i que passa pel punt ( )1,0,2

. Aquest pla serà:

1 2 4

: 1 3 0 : 8 10 19

2 1 2

x

y x y z

z

π π−

− = → + − = −− −




Donats el pla π d'equació x + 2y + 3z – 1 = 0, la recta r d'equacions 2 3

4

x z

y z

= − = +

i el punt

P = (2, 1, 1), calculeu: a) Unes equacions de la recta que passa per P i és perpendicular a π .

Anomenem a la nostra recta s . Aleshores ss vπ⊥ → � proporcional a ( )1,2,3nπ = →�

( )1,2,3sv =� .

Aleshores la recta s passa pel punt ( )2,1,1P = i té com a vector director ( )1,2,3sv =� per

tant, la seva equació vectorial és: ( ) ( ) ( ), , 2,1,1 1,2,3x y z λ= +

b) L'equació del pla que passa per P i és perpendicular a la recta r.

Anomenem al pla que busquem 'π . Com 'π és perpendicular a r, aleshores el vector normal

a 'π serà el vector director de r. És a dir, ' rn vπ =� �. Calculem aquest últim:

( ) ( )2 3 2 3: , , 2 3, 4,

4 4zx z x

r x y zy z y

λ λλ λ λ

λ== − = −

→ → = − + → = + = +

( ) ( ) ( ) ( ), , 3,4,0 2,1,1 2,1,1rx y z vλ→ = − + → =�

Ara sabem que el nostre pla 'π passa pel punt ( )2,1,1P = i que té com a vector normal

( )' 2,1,1nπ =� . Així: ( )2,1,1 '' : 2 0 2 2 1 1 0 6 0Px y z D D Dππ = ∈+ + + = → ⋅ + + + = → + = →

6 ' : 2 6 0D x y zπ→ = − → + + − =

c) Unes equacions de la recta que passa per P i talla perpendicularment r. Per trobar l’equació de la recta t que passa pel punt P i talla perpendicularment a r farem el següent:

1) Calculem l’equació del pla que passa per P i és perpendicular a r. (Calculat a l’apartat b)

2) Calculem el punt P’ on aquest pla talla la recta r. 3) Finalment calculem l’equació de la recta que passa pels punts P i P’.

Així: 1) Equació del pla que passa per P i és perpendicular a r: ' : 2 6 0x y zπ + + − = .

2) Punt de tall P’ on aquest pla 'π talla la recta r.

( )2 6 0

2 3 2 2 3 4 6 0 4 6 4 6 0

4

x y z

x z z z z z z z

y z

+ + − = = − → ⋅ − + + + − = → − + + + − = → = +

436 8 0 6 8z z z→ − = → = → =

84 13 3 32 3 2 3 3x z −= − = ⋅ − = − =

( ) ( ) ( )16 16 164 1 4 1 43 3 3 3 3 3 3 34 4 , , , , ' , ,y z x y z P− −= + = + = → = → = .

3) Equació de la recta que passa per ( )2,1,1P = i ( )161 43 3 3' , ,P −= .

( ) ( ) ( )16 7 131 4 13 3 3 3 3 3' ' , , 2,1,1 , ,PP P P −−= − = − =

�� proporcional a ( )7,13,1− .



Així la recta que busquem passa per ( )2,1,1P = i té com a vector director ( )7,13,1− . Per

tant, l’equació vectorial d’aquesta recta és: ( ) ( ) ( ), , 2,1,1 7,13,1x y z λ= + −

d) Unes equacions de la recta que passa per P, és paral·lela al pla π i tal que el seu vector director és perpendicular al de r. Anomenem a la nostra recta t. Si la recta t és paral·lela al pla π , aleshores el vector director

de la recta tv�

, serà perpendicular al vector normal del pla ( )1,2,3nπ =� .

Per altra banda, l’enunciat diu que la nostra recta t també ha de ser perpendicular a la recta r.

És a dir, tv�

serà perpendicular a ( )2,1,1rv =� .

Però tenim un mecanisme molt fàcil per trobar un vector tv�

perpendicular a ( )1,2,3nπ =� i a

( )2,1,1rv =� . Aquest és el producte vectorial. És a dir:

( ) ( ) ( )1,2,3 2,1,1 1 2 3 1,5, 3

2 1 1t r

i j k

v n vπ= × = × = = − −

��

� � �

Per tant, la nostra recta és: ( ) ( ) ( ): , , 2,1,1 1,5, 3t x y z λ= + − −



:3 2 0

x y zr

x y z

− − − = − − − =

i el pla : 2 2 0x y azπ − + + = , on a és un

paràmetre. a) Per a quin valor de a la recta i el pla són paral·lels? Quina serà llavors la distància entre el punt P = (1, 0, –1) de la recta i el pla? Anem a estudiar la posició relativa de la recta r i el pla π en funció del paràmetre a:

2 5 3 2 5 1 2 5 1 3

3 2 1 3 1 ' 1 3 1 2

2 2 2 1 2 1 2

x y z

x y z M i M

x y az a a

− − = − − − − − − = → = − − = − − − + = − − − −

Aprofitant que M és una matriu quadrada podem treballar per determinants. (Evidentment també podem optar per fer-ho pel mètode de Gauss)

2 5 1

1 3 1 3 0 3

2 1

M a a

a

− −= − − = − = → =

−

Sabem que per al valor 3a = la matriu M tindrà rang 2 però i la matriu M’? Anem a calcular el rang de la matriu M’ per aquest valor.

1 2 2 2 1

3 3 1

2

2

2 5 1 3 1 3 1 2 1 3 1 2 1 3 1 2

' 1 3 1 2 2 5 1 3 0 1 1 1 0 1 1 1

2 1 3 2 2 1 3 2 0 5 5 6 0 0 0 1

F F F F F

F F FM

↔ → −

→ −

− − − − − − − − = − − ≅ − − ≅ − ≅ − − − − − − −

Per tant, quan a=3 aleshores ( ) ( )2 3 ' . .Rang M Rang M S I r iπ= ≠ = → → paral·lels.



Ara ens demanen calcular la distància del punt ( )1,0, 1P = − al pla : 2 3 2 0x y zπ − + + = .

Sabem que la distància entre el punt ( )1 2 3, ,P p p p= i el pla : 0Ax By Cz Dπ + + + = és

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +. En el nostre cas:

( ) ( )( )22 2

2 1 0 3 1 2 2 0 3 2 1 14,

144 1 9 142 1 3d P π

⋅ − + ⋅ − + − − += = = =

+ ++ − +

b) Existeix algun valor de a per al qual la recta i el pla siguin perpendiculars?

La recta r i el pla π seran perpendiculars sii els vectors rv�

i nπ�

apunten en la mateixa direcció.

( )2, 1,n aπ = −� Calculem rv

�.

( ) ( ) ( )2 5 3 0: 2, 5, 1 1, 3, 1 2 5 1 2,1, 1

3 2 01 3 1

r

i j kx y z

r vx y z

− − − =→ = − − × − − = − − = − − − − = − −

��

�

Aleshores:

( ) ( ) 2 1 12,1, 1 2, 1,

2 1rr v proporcional n proporcional a aaππ −⊥ ↔ ↔ − − ↔ = =

−� �

Però donat que 2 1

2 1≠

− aleshores mai poden ser perpendiculars. Per tant no existeix cap

valor de a pel qual la recta i el pla siguin perpendiculars. c) Determineu el valor de a perquè la recta i el pla formin un angle de 30º. Sabem que aquest angle complirà la següent equació:

( ) ( )( ) ( )

( )( ) ( )2 22 2 2 2

2,1, 1 2, 1, 2 2 1 1 1sin sin sin

2,1, 1 2, 1, 2 1 1 2 1

r

r

a av n

v n a a

π

π

α α α− ⋅ − ⋅ + ⋅ − − ⋅⋅

= → = → =− − + + − ⋅ + − +

� �

� �

30º 2

2 2

4 1 4 11sin sin30º 6 5 2 4 1

26 5 6 5

a aa a

a a

αα =− − − −= → = = → ⋅ + = − − →

⋅ + ⋅ +

( ) ( ) ( )22 2 2 2 26 5 4 3 30 6 4 9 6 30 6 36 24 4a a a a a a a a→ ⋅ + = ⋅ − → + = − + → + = − + →

2 22 24 6 0 12 3 0 6 39a a a a a→ + − = → + − = → = − ±

8) PAU LOGSE 2000 Sèrie 3 Problema 2: Un quadrat de l'espai té tres dels seus vèrtexs consecutius situats en els punts de coordenades enteres P = (3, –2, 4), Q = (a, –1, a + 1) i R = (2, –3, 0).

a) Tenint en compte que els vectors QP��

i QR��

han de ser perpendiculars, calculeu el valor

del nombre enter a.

( ) ( ) ( )3, 2, 4 , 1, 1 3 , 1, 3QP P Q a a a a= − = − − − + = − − −��



( ) ( ) ( )2, 3,0 , 1, 1 2 , 2, 1QR R Q a a a a= − = − − − + = − − − −��

( ) ( )0 3 , 1, 3 2 , 2, 1 0QP QR QP QR a a a a⊥ ↔ ⋅ = ↔ − − − ⋅ − − − − = ↔��

( ) ( ) ( ) ( )( ) 2 23 2 1 2 3 1 0 6 3 2 2 3 3 0a a a a a a a a a a↔ − − − − + − − − = → − − + + − − + + = →

2

52

12 7 5 0

aa a

a

=→ − + = → =

Si P, Q i R són vèrtex d’un quadrat, aleshores els costats han de mesurar el mateix, per tant,

QP QR=��

. Comprovem aquesta condició pels valors obtinguts anteriorment:

• ( ) ( )1 2, 1,2 1, 2, 2 5a QP i QR QP QR= → = − = − − → = =��

• ( ) ( )5 71 1 12 2 2 2 2, 1, , 2,a QP i QR QP QR−−= → = − = − → ≠ →��

En aquest cas no formen

part d’un quadrat. Per tant, el valor buscat és : 1a = b) Calculeu l'equació del pla que conté aquest quadrat. P = (3, –2, 4), Q = (a, –1, a + 1) i R = (2, –3, 0).

( )( )2, 1,2

11, 2, 2

QPa

QR

= −= → = − −

��

��

El pla π que passa pels punts P, Q i R serà el pla que passa pel punt P i té com a vectors

directors QP��

i QR��

. Calculem-lo:

3 2 1

: 2 1 2 0 : 2 2 2 0

4 2 2

x

y x y z

z

π π−+ − − = → + − + =− −

c) Calculeu el quart vèrtex d'aquest quadrat. Podem observar en el dibuix adjunt que si anomenem T al quart vèrtex del quadrat (en gris)

tenim que T P QR= +��

. P = (3, –2, 4), Q = (1, –1, 2) i R = (2, –3, 0).

Aleshores ( ) ( ) ( )2, 3,0 1, 1,2 1, 2, 2QR R Q= − = − − − = − −��

.

Finalment: ( ) ( ) ( )3, 2,4 1, 2, 2 4, 4,2T P QR= + = − + − − = −��

d) Calculeu l'àrea d'aquest quadrat.

( ) ( ) ( )( )22 2 2 22 21, 2, 2 1 2 2Àrea quadrat Costat QR= = = − − = + − + − =��

( ) ( )2 22 21 2 2 1 4 4 9u= + − + − = + + =




Calculeu el peu de la recta perpendicular a la recta ( ) ( ) ( ): , , 1, 1,1 0,1,1r x y z λ= − + traçada

des del punt P=(1, 0, –1). L’estratègia per resoldre aquest problema serà la següent:

1) Calculem el pla π perpendicular a r i que

passa pel punt ( )1,0, 1P = − .

2) Calculem el punt Q on el pla π i la recta r

es tallen. 3) La solució al problema serà la recta s que

passarà pels punts P i Q (en vermell).

1) Càlcul del pla π perpendicular a r i que passa pel punt ( )1,0, 1P = − .

( )0,1,1 : 0 0 1 0Prr n v n y z D Dπ

π ππ π ∈⊥ → = → = → + + = → − + = →� � �

1 : 1 0D y zπ→ = → + + = 2) Càlcul del punt Q on el pla π i la recta r es tallen.

( ) ( ) ( ) 1 0 11 1 1: , , 1, 1,1 0,1,1

1 1 20 1 1

x xx y zr x y z

y z y zλ

− = = − + −= − + → = = → ≅ + = − = −

Per tant, el sistema que he de resoldre és:

( ) 12

1 0

1 2 1 0 2 1 0

2

y z

x z z z z

y z

+ + = = → − + + = → − = → = = −

( ) ( ) ( )3 3 31 1 12 2 2 2 2 22 2 , , 1, , 1, ,y z y y x y z Q− − −= − → = − → = → = → =

3) Càlcul de la recta que passa pels punts ( )1,0, 1P = − i ( )3 12 21, ,Q −= .

( ) ( ) ( )3 3 312 2 2 21, , 1,0, 1 0, ,PQ Q P − −= − = − − =

�� proporcional a ( )0, 1,1u = −�

Per tant la recta buscada serà: ( ) ( ) ( ): , , 1,0, 1 0, 1,1s x y z λ= − + −

10) PAU LOGSE 2000 Sèrie 6 Problema 1: Considereu la recta r de l'espai que passa pel punt P = (1, 1, 3) i té per vector director

( )1 , ,1v a a= −�. Sigui π el pla que té per equació 2x + y – z = 1.

a) Determineu per a cada valor del paràmetre a la posició relativa de la recta r respecte al pla π (paral·lela, continguda o amb un punt d'intersecció).

Sempre tenim l’opció de procedir mitjançant matrius però procuraré fer un mètode més ràpid. En el dibuix adjunt es veu que r i π paral·lels o r

continguda en π sii rv�

i nπ�

ortogonals 0rv nπ↔ ⋅ =� �.

Comprovem açò últim:

( ) ( ) ( )1 , ,1 2,1, 1 2 1 1 2 2 1 1rv n a a a a a a aπ⋅ = − ⋅ − = − + − = − + − = − +� �



0 1 0 1rv n a aπ⋅ = → − + = → =� �

No hem acabat, sabem que pel valor a=1 la recta r estarà continguda en el pla o serà paral·lela a aquest però, en quin dels dos casos ens trobem? Serà suficient comprovar si el punt P que pertany a r també pertany al pla o no.

( )1,1,3P = i : 2 1x y zπ + − = substituint: 2 1 1 3 2 1 3 0 1 P rπ π⋅ + − = + − = ≠ → ∉ → �

Per tant: Si 1a = aleshores r paral·lela a π i si 1a ≠ aleshores r i π secants. b) Hi ha alguna de les rectes r que sigui perpendicular al pla π ?

Evidentment la recta r serà perpendicular al pla π sii els vectors de r i de π apunten en la mateixa direcció, és a dir, si aquestos vectors són proporcionals. Aleshores:

( )1 , ,1rv a a= −� i ( )2,1, 1nπ = −�

131 2 1 31 1

1 12 1 1 1

aa a aa a

a a a

=− = = − = = → ≅ ≅ − = = −− = −

Per tant no hi ha cap valor del paràmetre a que faci que la recta r sigui perpendicular al pla π . c) Calculeu la distància que hi ha entre el punt P i el pla π .

Donat un punt ( )1 2 3, ,P p p p= i un pla : 0Ax By Cz Dπ + + + = tenim que:

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +. En el nostre cas ( )1,1,3P = i : 2 1 0x y zπ + − − = i per

tant: ( )( )22 2

2 1 1 3 1 2 1 3 1 1 1 6,

64 1 1 6 62 1 1d P π

⋅ + − − + − − −= = = = =

+ ++ + −

11) PAU LOGSE 2001 Sèrie 2 Qüestió 3: Donats els punts de l'espai A = (2, 0, 0), B = (0, 1, 0) i C = (0, 0, 3). a) Determineu l'equació del pla π que els conté.

• Per calcular l’equació del pla π que passa pels punts A, B i C necessitem un punt i dos vectors directors. • Calculem dos vectors:

( ) ( ) ( )0, 1, 0 2, 0, 0 2, 1, 0AB B A= − = − = −��

( ) ( ) ( )0, 0, 3 2, 0, 0 2, 0, 3AC C A= − = − = −��

• Finalment calculem l’equació del pla π que passa pel punt ( )2, 0, 0A= i amb vectors

directors ( )2, 1, 0AB= −��

i ( )2, 0, 3AC = −��

.

( )2 2 2

: 1 0 0 : 3 2 0 0 2 0 6 0 : 3 6 2 6 0

0 3

x

y x z y x y z

z

π π π− − −

= → − + + + − + = → + + − =



b) Calculeu l'equació de la recta r perpendicular al pla π i que passa per l'origen.

• Si la recta r és perpendicular al pla π , aleshores el vector director de la recta rv

� coincidirà

amb el vector normal al pla π que anomenarem nπ�

. • Càlcul del vector normal al pla π :

( ) ( )2, 1, 0 2, 0, 3 2 1 0

2 0 3

i j k

n AB ACπ = × = − × − = − =−

��

��

( )3 0 0 2 0 6 3 6 2 3, 6, 2i k j k i j i j k= − − + − + = + + =� � ��

• Per tant, busquem la recta r que té vector director ( )3, 6, 2rv =� i que passa per l’origen

( )0, 0, 0O = . Aquesta recta és: ( ) ( ) ( ): , , 0,0,0 3,6,2r x y z λ= +



12) PAU LOGSE 2001 Sèrie 4 Qüestió 1: Determineu per a quins valors del paràmetre a el pla π : ax + 2y + z = a és paral·lel a la recta

r : 1

1

x ay z

ax z a

− + = + = +

• El pla π i la recta r seran paral·lels sempre i quan el sistema que formin tots dos sigui incompatible. És a dir, ens estan demanant els valors del paràmetre a que facin que el sistema

2

1

1

ax y z a

x ay z

ax z a

+ + = − + = + = +

sigui incompatible.

• Aleshores hem de discutir el sistema anterior en funció dels valors del paràmetre a .

2 1 2 2 1

3 3 1

2

2

2 1 1 1 1 1 1 1

' 1 1 1 2 1 0 2 1 0

0 1 1 0 1 1 0 1 1

F F F F aF

F F aF

a a a a

A a a a a a

a a a a a a

↔ → −

→ −

− − = − ≅ ≅ + − + + −

La matriu A tindrà rang diferent de 3 sii les dues últimes files són proporcionals. Aleshores:

( )( ) ( ) ( )( )2

2 2 2 22

2 12 1 1 1 2 0

1

a aa a a a a a a

a a

+ −= → + − = − → − + − = →−

( )1 2 0 1 0 1a a a→ − ⋅ = → − = → =

Fins ara sabem que si 1a = aleshores ( ) 3Rang A < i que si 1a ≠ aleshores

( ) ( )' 3 º . . . iRang A Rang A n incògnites S C D rπ= = = → → es tallaran en un punt.

Per tant, el que ens queda per estudiar és si en el cas 1a = el sistema és compatible indeterminat o incompatible. Així: • Estudi del sistema quan 1a = : En aquest cas:

2 2 1

3 3 1

1 2 1 1 1 2 1 1

' 1 1 1 1 0 3 0 0

1 0 1 2 0 2 0 1

F F F

F F FA

→ −

→ −

= − ≅ − → −

Podem observar que les equacions 2 i 3 són

incompatibles, és a dir, ( ) ( )2 3 ' . .Rang A Rang A S I= ≠ = →

Per tant, l’únic valor de a per al que la recta i el pla són paral·lels és 1a =

NOTA: Com en tota discussió d’un sistema d’equacions lineals, donat que la matriu de coeficients era una matriu quadrada, era més ràpid calcular el seu determinar i estudiar directament els valors de a que fessin nul aquest determinant. 13) PAU LOGSE 2001 Sèrie 4 Problema 2: Sigui π el pla d'equació x – y + 2z = 3 i P el punt (1, 1, 0). a) Calculeu la distància d de P a π .



Donat un punt ( )1 2 3, ,P p p p= i un pla : 0Ax By Cz Dπ + + + = tenim que:

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +. En el nostre cas ( )1,1,0P = i : 2 3 0x y zπ −− + = i per

tant: ( )( )22 2

1 1 2 0 3 3 3 3 3 6 6,

6 21 1 4 6 61 1 2d P π

− + ⋅ − − −= = = = = =

+ ++ − +

b) Determineu l'equació de l'altre pla π ' paral·lel a π que també dista d del punt P. Sabem que qualsevol pla 'π paral·lel a : 2 3 0x y zπ − + − = té una equació del tipus

' : 2 0x y z kπ − + + = .

Per tant, cal determinar k per a que ( ) 6, '

2d P π = . Aleshores:

( )( )22 2

1 1 2 06 6 6 6 6, ' 3 3

2 2 2 261 1 2

k kd P k k kπ

− + ⋅ + ⋅= → = = → = → = = → = ±+ − +

Com pel pla π el paràmetre k ja valia 3− , el valor de k pel pla 'π és 3k = i per tant tenim

que la resposta al problema és el pla ' : 2 3 0x y zπ − + + =

c) Determineu l'equació de la recta r perpendicular a π que passa per P.

Per ser la recta r perpendicular al pla π tenim que el vector director de r serà el vector normal

al pla π , és a dir, ( )1, 1, 2rv nπ= = −� �.

Així, la recta r és la recta que passa pel punt ( )1, 1, 0P= i té vector director ( )1, 1, 2rv = −�

, per tant: ( ) ( ) ( ): , , 1,1,0 1, 1,2r x y z λ= + − o si volem escriure-la amb l’equació continua

seria 1 1 0

:1 1 2

x y zr

− − −= =−

d) Calculeu la intersecció de la recta r amb el pla π .

Per calcular el punt de intersecció entre r i π solament cal resoldre el sistema d’equacions que formen tots dos.

111 1

11 2

1 1 2 21 1 0:

1 1 2 2 2 2 2

yx

x z

x y x y x yx y zr

x z x z

−−−

−

= → − + = − → − − = − → + =− − − = = → →− = → − = → − =

2:

2 2

x yr

x z

+ =→ − =



Per tant, els sistema d’equacions format per r i π és:

2

2 2

2 3

x y

x z

x y z

+ = − = − + =

3 3 22 2 1

3 3 1

21 1 0 2 1 1 0 2 1 1 0 2

' 2 0 1 2 0 2 1 2 0 2 1 2

1 1 2 3 0 2 2 1 0 0 3 3

F F FF F F

F F FA

→ −→ −

→ −

= − ≅ − − − ≅ − − − → − −

3 3 1z z= → = 1

2 2 2 1 2 2 12

y z y y y− − = − → − − = − → − = − → =

1 1 32 2 2

2 2 2x y x x x+ = → + = → = − → =

Així, el punt entre la recta r i el pla π és: 3 1

' , , 12 2

P =


Considereu a l'espai la recta r d'equacions 2 3 1

2 3 1

x y z− + += =− −

i la recta s d'equacions

4 1 4

2 3 1

x y z+ − += =−

a) Determineu el punt de tall de la recta r amb el pla z = 0.

( ) ( )( ) ( )

3 2 2 3 3 6 2 6 3 2 02 3 1:

2 2 2 2 02 3 1 1 2 2 1

x y x y x yx y zr

x z x zx z

− − = + − + = + + = − + + = = → → → − + = + + =− − − − = +

Així el punt de tall entre la recta r i el pla 0z = serà la solució del sistema:

3 2 0

2 0

0

x y

x z

z

+ = + = =

que té com a única solució el punt ( ) ( ), , 0,0,0x y z =

b) Comproveu que les rectes r i s són paral·leles i calculeu la distància entre elles.

Per comprovar que r i s són paral·leles mirarem que els seus vectors directors rv�

i sv�

siguin

proporcionals i que un punt d’una recta no pertanyi a l’altra.

Tenim que ( )2, 3, 1rv = − −� i ( )2,3,1sv = −�

. 2 3 1

2 3 1 r sv i v− −= = →

−� �

proporcionals r i s

paral·leles o coincidents.

( )2, 3, 1P r= − − ∈ anem a comprovar si aquest punt també pertany a l’altra recta s.

( )2, 3, 14 1 4 2 4 3 1 1 4 6 4 3:

2 3 1 2 3 1 2 3 1Px y z

s FALS= − −+ − + + − − − + −= = → = = → = =− − −

Per tant, P s∉ i r i s paral·leles. • Càlcul de la distància entre les dues rectes:



Per calcular la distància entre dues rectes paral·leles és suficient calcular la distància d’un punt

d’una a l’altra recta. Així agafem ( )0,0,0P r= ∈ ( )4,1, 4Q s= − − ∈ i ( )2, 3, 1v = − −� vector

director de les rectes i tenim:

( ) ( ) ( ) ( )( )

( )( ) ( )2 22

4,1, 4 2, 3, 1 13, 12,10, ,

2, 3, 1 2 3 1

PQ vd r s d Q r

v

× − − × − − − −= = = = =

− − + − + −

��

�

413 118

214= =

c) Quina és l'equació del pla que conté les dues rectes?

Com r i s paral·leles tindran el mateix vector director ( )2, 3, 1rv = − −�.

El pla π que contindrà aquestes dues rectes serà el pla que té com a vector director

( )2, 3, 1rv = − −� i que passa pels punts ( )2, 3, 1P r= − − ∈ i ( )4,1, 4Q = − − , és a dir:

El pla π que passa per ( )2, 3, 1P r= − − ∈ i té com a vectors directors ( )2, 3, 1rv = − −� i PQ��

.

Però ( ) ( ) ( )4,1, 4 2, 3, 1 6,4, 3PQ Q P= − = − − − − − = − −��

, per tant:

2 2 6

: 3 3 4 0 13 12 10 0

1 1 3

x

y x y z

z

π− −+ − = → + − =+ − −

(Nota, també haguéssim arribat al mateix resultat i amb càlculs relativament més fàcils agafant

com a punt P de la primera recta ( )0,0,0P= .

d) Calculeu la distància del pla anterior a l'origen de coordenades. És evident que el pla anterior passa per l’origen de coordenades, per tant aquesta distància és zero. 15) PAU LOGSE 2002 Sèrie 1 Qüestió 3: Comproveu que la recta que passa pels punts A = (4, 0, 0) i B = (0, 2, 2) és paral·lela al pla d'equació x – 3y + 5z = 2, i calculeu la distància entre la recta i el pla. • La recta que r passa pels punts A i B tindrà vector director:

( ) ( ) ( )0,2,2 4,0,0 4,2,2AB B A= − = − = −��

El vector normal al pla : 3 5 2x y zπ − + = és ( )1, 3,5nπ = −�

• Si aquests dos vectors ( )4,2,2AB= −��

i ( )1, 3,5nπ = −� fossin perpendiculars, aleshores ja

estaríem en condicions d’afirmar que la recta i el pla o bé son paral·lels o bé la recta està continguda en el pla.

( ) ( )4,2,2 1, 3,5 4 6 10 0AB n AB nπ π⋅ = − ⋅ − = − − + = → ⊥ →��

r i π paral·lels o r està

continguda en π . Finalment, per decidir si estem en el cas en que r i π són paral·lels o bé estem en el cas en que r està continguda en π , agafem un punt de la recta r i el substituïm en l’equació de π .

( )4,0,0A r= ∈ i 4 3 0 5 0 4 2 A rπ− ⋅ + ⋅ = ≠ → ∈ → paral·lela a π



NOTA: Una altra manera de resoldre aquest problema seria trobar l’equació de la recta i estudiar la posició relativa entre la recta i el pla. Quedaria així:

La recta r que passa per ( )4,0,0A= i ( )0,2,2B= té vector director ( )4,2,2AB= −��

i

passa per ( )4,0,0A= , per tant, l’equació d’aquesta recta és 4 0 0

:4 2 2

x y zr

− − −= =−

, d’on

obtenim que: 24

4 2

244 2

2 8 4 2 4 8 2 4

2 8 4 2 4 8 2 4

yx

x z

x y x y x y

x z x z x z

÷−−

÷−−

= → − = − → + = → + =

= → − = − → + = → + =

Així, el sistema format per la recta i el pla és:

3 5 2 1 3 5 2 1 3 5 2

2 4 ' 1 2 0 4 0 5 5 2

2 4 1 0 2 4 0 3 3 2

x y z

x y A

x z

− + = − − + = → = ≅ −

+ = −

Podem observar que les dues últimes equacions són incompatibles entre si, per tant, la recta i el pla no tenen cap punt en comú, és a dir, la recta és paral·lela al pla. 16) PAU LOGSE 2002 Sèrie 1 Problema 2: Considerem el cub de vèrtexs A, B, C, D, E, F, G, H que té l'aresta de longitud 4 dm. a) Determineu l'equació del pla inclinat EHBC si prenem com a origen de coordenades el vèrtex D i com a eixos de coordenades DA, DC i DH en aquest ordre, tenint en compte que el sentit positiu de cada un d'ells és el que sortint de l'origen D va cap a A, C i H, respectivament. • Si el cub té aresta igual a 4, aleshores tenim que:

( )4,4,0B= , ( )0,4,0C = , ( )4,0,4E = i ( )0,0,4H =

• Determinem l’equació del pla π que passa pels punts, per exemple B, C i D:

( ) ( ) ( )0,4,0 4,4,0 4,0,0BC C B= − = − = −��

( ) ( ) ( )4,0,4 4,4,0 0, 4,4BE E B= − = − = −��

Calculem π com el pla que passa pel punt ( )4,4,0B= i té com a vectors directors BC��

i

BD��

.

( ) ( )4 4 4

4 4 4 1: 4 0 4 0 1 4 0 4 4 0

4 10 0 4

xy y

yz z

z

π− − −

− − − −− − = → − ⋅ − ⋅ = → ⋅ ⋅ = →−

4 10 4 0 4

1

yy z y z

z

− −→ = → − + = → + =

b) Calculeu les equacions de les diagonals CE i AG i utilitzeu-les per calcular les coordenades del seu punt d'intersecció. .

• Diagonal que passa per ( )0,4,0C = i ( )4,0,4E = : (En blau)



( ) ( ) ( ) ( )4,0,4 0,4,0 4, 4,4 1, 1,1CE E C CE= − = − = − → −��

�

41 1

1 1

4 40 4 0:

1 1 1 0

yx

x z

x y x yx y zr

x z x z

−− = → − = − → + =− − − = = → − = → = → − =

4:

0

x yr

x z

+ =→ − =

• Diagonal que passa per ( )4,0,0A= i ( )0,4,4G = : (En vermell)

( ) ( ) ( ) ( )0,4,4 4,0,0 4,4,4 1,1,1AG G A AG= − = − = − → −��

�

41 1

1 1

4 4 44 0 0: :

01 1 1 0

yx

y z

x y x y x yx y zs s

y zy z y z

−− = → − = − → + = + =− − − = = → → − =− = → = → − =

• Resolem el sistema format per les dues rectes r i s :

4: 4 1 1 0 4 1 1 0 4

00 ' 1 0 1 0 0 1 1 4

40 0 1 1 0 0 1 1 0:

0

x yr x y

x zx z A

x yy zs

y z

+ = + = − = ≅ − = → = − ≅ − − − ≅ + = − = − − − =

1 1 0 4

0 1 1 4 2 4 2

0 0 2 4

z z

≅ − − − → − = − → = − −

4 2 4 2 2y z y y y− − = − → − − = − → − = − → =

4 2 4 2x y x x+ = → + = → =

Per tant, el punt de tall entre les dues rectes és ( ) ( ), , 2,2,2x y z =

NOTA: Per construcció, cadascuna de les dues rectes va des d’un vèrtex del cub al vèrtex oposat. Això fa que aquestes dues rectes s’hagin de tallar en el centre del cub que evidentment

és el punt ( )2,2,2 .

17) PAU LOGSE 2002 Sèrie 2 Qüestió 4: Calculeu l'angle que forma el pla x – 2y + z = 1 amb la recta determinada per les equacions

1

2

x t

y t

z

= = + =

Sigui el pla : 2 1x y zπ − + = , aleshores el seu vector normal és ( )1, 2,1nπ = −�.

Sigui la recta : 1

2

x t

r y t

z

= = + =

, aleshores el seu vector director és ( )1,1,0rv =� .



Podem calcular l’angle agut (*) entre aquests dos vectors mitjançant el seu producte escalar:

�( ) �( ) ( ) ( )( ) ( )1, 2,1 1,1,0

cos , cos ,1, 2,1 1,1,0

rr r r r

r

n vn v n v n v n v

n vπ

π π π ππ

− ⋅⋅⋅ = ⋅ → = = =

⋅ −

� ��

� �

1 2 0 1 1 3

66 2 12 2 3

− + −= = = = →

⋅�( ) �3 3

cos , , cos 73,22º6 6r rn v n v arπ π

= → =

� � � �≃

Aleshores, l’angle que formen el pla π i la recta r és

90º 73,22º 16,78º− = (FIGURA)

(*) Per a forçar que l’angle sigui agut, és a dir, menor de 90º, hem d’agafar el producte escalar en valor absolut. En el cas de l’angle entre dos vectors, que pot ser obtús, aleshores prendríem la fórmula

�( )cos ,r r rn v n v n vπ π π⋅ = ⋅� � � � � �.

18) PAU LOGSE 2002 Sèrie 2 Problema 1: Considereu les rectes r i s amb les equacions següents:

r:3 0

2 2 0

x y

x z

− + = − + =

s:13 0

2 3 0

y

x z

+ = − − =

a) Calculeu, de cada una de les rectes, un punt i un vector director.

Per aconseguir-ho cal ficar dues incògnites qualsevol de les ( ), ,x y z en funció de la 3a.

( )33 0

:2 3 2 0 2 6 2 0 2 42 2 0

x yx yr

y z y z z yx z

= −− + =→ − − + = → − − + = →→ = −− + =

( ) ( ) ( ) ( ) ( ), , 3, ,2 4 , , 3,0, 4 1,1,2yx y z y y y x y zλ λ== − − → = − − +

( ) ( )1 13 3 1

3

0: , , 2 3, ,

2 3 0 2 3zy y

s x y z z zx z x z

λ−

=−+ = =

→ → = + → − − = = +

( ) ( ) ( )13, , 3, ,0 2,0,1x y z λ−→ = +

b) Determineu si existeix cada un dels objectes següents i en cas afirmatiu calculeu la seva equació:

i) El pla paral·lel a la recta s que conté la recta r. Sigui π aquest pla.

Per ser paral·lel a la recta s, el vector director de s serà vector director de π . Així ( )2,0,1sv =�

vector director de π .

Si π conté la recta r aleshores el punt ( )3,0, 4P = − − que pertany a r també pertany a π . I

el vector director de r, ( )1,1,2rv =� també serà vector director de π .

Així:



( ) ( )3 2 1

: 0 1 0 2 4 3 4 2 8 3 4

4 1 2

x

y y z x y y z x y

z

π+

= → + + − + − = + + − − − =+

3 2 5 0 : 3 2 5 0x y z x y zπ= − − + + = → + − − =

ii) El pla perpendicular a la recta s que conté la recta r.

En la figura podem observar que per a que existeixi aquest pla 'π , les rectes r i s han de ser perpendiculars.

Però ( ) ( )1,1,2 2,0,1 2 0 2 4 0r sv v⋅ = ⋅ = + + = ≠ →� �r i s no perpendiculars,

per tant, aquest pla no existeix.

iii) La recta perpendicular a les rectes r i s que passa per (0, 0, 0). Si anomenem t a la recta buscada, aleshores sabem que el seu vector director tv

� serà

perpendicular als vectors directors de r i de s. És a dir:

( ) ( )1,1,2 2,0,1 1 1 2 0 4 2 0

2 0 1t r s

i j k

v v v i k j k i j= × = × = = + + − − − =

��

� ��

( )3 2 1, 3, 2i j k= + − = −��

Per tant, la recta buscada és ( ) ( ) ( ), , 0,0,0 1,3, 2x y z λ= + −


Considereu els plans d'equacions: 1 : 2 3x y zπ + − = i ( )2 : 2 2 4ax a y zπ + − + = .

a) Hi ha algun valor del paràmetre a per al qual la intersecció dels plans 1π i 2π no és una

recta? Dos plans o bé es tallen formant una recta o bé són paral·lels o coincidents. És a dir, no es poden tallar en un punt. Si 1π i 2π no es tallen formant una recta aleshores són

paral·lels o coincidents. Però en aquests dos casos (paral·lels o coincidents) els seus vectors normals apuntaran en la mateixa direcció i per tant seran proporcionals.

Així, estudiem el cas en que els vectors ( )1 1,2, 1n = −� i

( )2 , 2, 2n a a= −� són proporcionals.



1 12

2 12 2

2 21 2 1

2 2 4 2 2a

a

a a

a a a a

−

−−

= → = − → = −−= = → →− = → = − + → = − Per tant, si que hi ha un valor del

paràmetre a pel qual els dos plans no formen una recta, aquest valor és 2a = −

b) Calculeu un vector director de la recta que s'obté quan es fa la intersecció de 1π i 2π per al

valor del paràmetre a = 0. Quan tenim una recta donada com a intersecció de dos plans. Podem calcular el vector director de la recta amb el producte vectorial dels vectors normals dels plans. Així:

( )( )( )

11 10

2 2 2

1,2, 1: 2 3 : 2 3

: 2 2 4 : 2 2 4 0, 2,2a

nx y z x y z

ax a y z y z n

π ππ π

== −+ − = + − = → → + − + = − + = = −

�

�

( ) ( ) ( )1 2 1,2, 1 0, 2,2 1 2 1 4 2 0 0 2 2 2, 2, 2

0 2 2

i j k

n n i k j k i j× = − × − = − = − + − − − = − −−

��

� ��


Considereu la recta r d'equacions: 5 7

13 4

y zx

− −− = =− −

. Calculeu els punts d'aquesta recta

situats a una distància 3 del punt A = (1, 0, 1). En el gràfic podem observar que generalment hi ha dos punts d’una recta que estan a una determinada distància d’un tercer.

( ) ( ) ( )5 7: 1 , , 1,5,7 1, 3, 4

3 4

y zr x x y z λ− −− = = → = + − −

− −Per tant, tots els punts de la recta r són de la forma: ( )1 , 5 3 , 7 4λ λ λ+ − − .

Sigui un punt P de la recta r, P tindrà la forma: ( )1 , 5 3 , 7 4λ λ λ+ − −

Aleshores la distància entre P i A serà: ( ),d A P AP=��

( ) ( ) ( )1 , 5 3 , 7 4 1, 0, 1 , 5 3 , 6 4AP P A λ λ λ λ λ λ= − = + − − − = − −��

( ) ( ) ( ) ( )2 22, , 5 3 , 6 4 5 3 6 4d A P AP λ λ λ λ λ λ= = − − = + − + − =��

2 2 2 225 30 9 36 48 16 26 78 61λ λ λ λ λ λ λ= + − + + − + = − +

( ) 262 2 2, 3 26 78 61 3 26 78 61 9 26 78 52 0d A P λ λ λ λ λ λ ÷= → − + = → − + = → − + = →

2 13 2 0

2

λλ λ

λ=

→ − + = → =



( )( )

( )

1 2,2,31 , 5 3 , 7 4

2 ' 3, 1, 1

PP

P

λλ λ λ

λ

= → =

= + − − → = → = − −


Considereu el punt P = (5, –2, 9) i la recta 1 1

:2 3 6

x y zr

− += =− −

a) Calculeu l’equació de la recta s que talla perpendicularment r i que passa per P. b) Calculeu el punt de tall Q entre les rectes r i s. Resoldrem tots dos apartats a la vegada. • Calculem el pla π perpendicular a la recta r i que passa per P:

( ): 2 3 6 0

2 5 3 2 6 9 0

Pr x y z k

k

ππ π ∈⊥ → − − + + = →→ − ⋅ − ⋅ − + ⋅ + = →

10 6 54 0 50 0 50

: 2 3 6 50 0

k k k

x y zπ→ − + + + = → + = → = − →→ − − + − =

• Calculem el punt de tall Q entre el pla π i la recta r: 11

2 3

212 6

3 3 2 2 3 2 51 1:

2 3 6 6 6 2 6 2 6 3 3

yx

x z

x y x yx y zr

x z x z x z

+−− −

÷−−

= → − + = − − → − + = −− + = = → − − = → − = − → + = → + =

1 1 2 2 1

2 2 3 3 1

3

2

2 3 6 50 0 2 3 6 50 6 9 18 150

3 2 5 ' 3 2 0 5 6 4 0 10

3 3 3 0 1 3 6 0 2 6

F F F F F

F F F F F

x y z

x y A

x z

→ → −

→ → +

− − + − = − − − − − + = − → = − − ≅ − − ≅

+ =

3 3 22 2

3 3

9

13

6 9 18 150 6 9 18 150

0 13 18 160 0 117 162 1440

0 9 20 156 0 117 260 2028

F F FF F

F F

→ +→

→

− − − − ≅ − − ≅ − − ≅ − −

6 9 18 150

0 117 162 1440

0 0 98 588

− − ≅ − −

58898 588 6

98z z z= → = → =

117 162 1440 117 162 6 1440 117 972 1440 117 468y z y y y− = − → − ⋅ = − → = − → = − →

4684

117y y

−→ = → = −

( )6 9 18 150 6 9 4 18 6 150 6 36 108 150x y z x x− − + = → − − ⋅ − + ⋅ = → − + + = →

6 6 1x x→ − = → = −

Així, la recta r i el pla π es tallen en el punt ( )1, 4,6Q = − − .

• Finalment, la recta buscada, és la recta que passa per ( )5, 2,9P= − i ( )1, 4,6Q = − − :

( ) ( ) ( )1, 4,6 5, 2,9 6, 2, 3PQ Q P= − = − − − − = − − −��



( ) ( ) ( ): , , 5, 2,9 6,2,3s x y z λ= − +

22) PAU LOGSE 2003 Sèrie 3 Qüestió 4: Considereu els punts de l’espai A = (0, –2a – 1, 4a – 2), B = (1, –3, 4), C = (3, –5, 3). a) Comproveu que el triangle de vèrtexs A, B i C és rectangle en B per a qualsevol valor de a.

El triangle de vèrtex A, B i C serà rectangle en B si els vectors BA��

i BC��

són perpendiculars. Aquests vectors seran perpendiculars si el seu producte escalar és zero. Aquesta perpendicularitat no dependrà del valor del paràmetre a, si el producte escalar anterior és sempre zero i no depèn de a.

( ) ( ) ( )0, 2 1, 4 2 1, 3, 4 1, 2 2, 4 6BA A B a a a a= − = − − − − − = − − + −��

( ) ( ) ( )3, 5, 3 1, 3, 4 2, 2, 1BC C B= − = − − − = − −��

( ) ( )1, 2 2, 4 6 2, 2, 1 2 4 4 4 6 0BA BC a a a a⋅ = − − + − ⋅ − − = − + − − + =��

Per tant, el triangle de vèrtex A, B i C és rectangle en B per a qualsevol valor de a. b) Calculeu els valors de a que fan que aquest triangle sigui isòsceles. Per a que un triangle de vèrtex A, B i C rectangle en B sigui isòsceles s’ha

de complir que els dos catets siguin iguals, és a dir, que els vectors BA��

i

BC��

mesurin el mateix.

( ) ( ) ( ) ( )2 2 21, 2 2, 4 6 1 2 2 4 6BA a a a a= − − + − = − + − + + − =

��

2 2 21 4 8 4 16 48 36 20 56 41a a a a a a= + − + + − + = − +

( ) ( ) ( )2 222, 2, 1 2 2 1 4 4 1 9BC = − − = + − + − = + + =��

2 220 56 41 9 20 56 41 9BA BC a a a a= → − + = → − + = →��

2

45

220 56 32 0

aa a

a

=→ − + = →

=

23) PAU LOGSE 2003 Sèrie 3 Problema 2: Un segment d’extrems A = (5, 3, 1) i B = (4, 2, –1) es divideix en tres parts iguals mitjançant dos plans perpendiculars a aquest segment. Calculeu les equacions dels dos plans i la distància entre ells.



• Pel fet de que els plans π i 'π siguin perpendiculars al segment AB tindrem que el vector

normal a aquests plans serà el vector AB��

.

És a dir, ( ) ( ) ( )' 4, 2, 1 5, 3, 1 1, 1, 2n n AB B Aπ π= = = − = − − = − − −��

• Calculem ara, els punts C i D que divideixen el segment AB en tres parts iguals.

( ) ( ) ( )1 1 1 1 2 14 8 15, 3, 1 1, 1, 2 5, 3, 1 , , , ,

3 3 3 3 3 3 3 3C A AB

− − − = + = + − − − = + =

��

( ) ( ) ( )2 2 2 2 4 13 7 15, 3, 1 1, 1, 2 5, 3, 1 , , , ,

3 3 3 3 3 3 3 3D A AB

− − − − = + = + − − − = + =

��

• Finalment calculem l’equació dels plans π i 'π :

π passa pel punt 14 8 1

, ,3 3 3

C =

i amb vector director ( )1, 1, 2AB = − − −��

. Així:

14 8 1 24: 2 0 2 0 0 8 0

3 3 3 3Cx y z k k k kππ ∈ − −− − − + = → − − ⋅ + = → + = → − + = →

8 : 2 8 0k x y zπ→ = → − − − + =

'π passa pel punt 13 7 1

, ,3 3 3

D− =

i amb vector director ( )1, 1, 2AB = − − −

��. Així:

' 13 7 1 18' : 2 ' 0 2 ' 0 ' 0 6 ' 0

3 3 3 3Dx y z k k k kππ ∈ − − −− − − + = → − − ⋅ + = → + = → − + = →

' 6 ' : 2 6 0k x y zπ→ = → − − − + =

La distància entre els dos plans π i 'π serà la mateixa que la distància entre els punts C i D que a la vegada serà un terç de la distància entre els punts A i B. Així:

( ) ( ) ( ) ( )1 1 1, ' , , 1, 1, 2

3 3 3d d C D d A B ABπ π = = = = − − − =

��

( ) ( ) ( )2 2 21 61 1 2

3 3= − + − + − =




Determineu l'equació del pla que conté a la recta 1 12

yx z− = = + i passa per l'origen de

coordenades. Si trobem dos punts A i B de la recta. Com el pla també passa per l’origen de coordenades, ja tindrem 3 punts que determinaran el nostre pla.

• Trobem aleshores dos punts de la recta 1 12

yx z− = = +

Evidentment un punt pot ser ( )1,0, 1A= − .

Si a aquest punt A li sumem el vector director de la recta, obtindrem un altre punt de la recta.

Així, ( ) ( ) ( )1,0, 1 1,2,1 2,2,0B A v= + = − + =�

• Finalment calculem l’equació del pla que passa pels punts ( )1,0, 1A= − , ( )2,2,0B= i

( )0,0,0O = .

( ) ( ) ( )1,0, 1 0,0,0 1,0, 1OA A O= − = − − = −��

( ) ( ) ( )2,2,0 0,0,0 2,2,0OB B O= − = − =��

2

0 1 2 1 2

: 0 0 2 0 0 2 0 2 2 2 0 2 2 2 0

0 1 0 1 0

x x

y y y z x x y z

z z

π ÷

−− = → = → − + + = → − + = →− − −

0x y z→ − + =

25) PAU LOGSE 2004 Sèrie 1 Qüestió 2: Considereu els punts de l’espai A(0, 0, 1), B(1, 1, 2) i C(0, –1, –1). a) Trobeu l’equació del pla ABC. • Per calcular l’equació del pla utilitzarem un punt i dos vectors. Així:

( ) ( ) ( )1,1,2 0,0,1 1,1,1AB B A= − = − =��

( ) ( ) ( )0, 1, 1 0,0,1 0, 1, 2AC C A= − = − − − = − −��

• El pla π que passa pel punt ( )0,0,1A= i té com a vectors directors ( )1,1,1AB =��

i

( )0, 1, 2AC = − −��

és:

0 1 0 1 0

: 0 1 1 0 1 1 0 2 1 2 0

1 1 2 1 1 2

x x

y y x z x y

z z

π−− − = → − = → − − + + + = →− − − −

: 2 1 0x y zπ→ − + − + =



b) Si D és el punt de coordenades (k, 0, 0), quant ha de valer k per tal que els quatre punts A, B, C i D siguin coplanaris? Els 4 punts A, B, C i D seran coplanaris sempre i quan el punt D estigui en el pla que determinen A, B i C. Per tant, solament hem d’obligar a que el punt D passi pel pla anterior.

( ),0,0: 2 1 0 2 0 0 1 0 1 0 1D kx y z k k kπ =→ − + − + = →− + ⋅ − + = → − + = → =

26) PAU LOGSE 2004 Sèrie 3 Problema 2: Tenim quatre punts a l’espai: A(0, 0, 0); B(0, 0, 2); C(0, 2, 0) i D(2, 0, 0). Es demana: a) representeu gràficament els quatre punts;

b) calculeu el volum del tetràedre (piràmide de base triangular) ABCD;

Si calculem els vectors AB��

, AC��

i AD��

, sabem que el mòdul del producte mixte d’aquestos vectors és el volum del paral·lelepípede que formen. Per altra part, el volum del tetràedre o piràmide de base triangular que formen tres vectors és la sisena part del volum del paral·lelepípede, per tant:

( ) ( ) ( )0,2,0 0,0,0 0,2,0AC C A= − = − =��

( ) ( ) ( )2,0,0 0,0,0 2,0,0AD D A= − = − =��

·

0 0 21 1 1 1 1 8 4

, , 0 2 0 8 86 6 6 6 6 6 3

2 0 0Piràmide Paral lelepípedeV V AB AC AD = = ⋅ = ⋅ = ⋅ − = ⋅ = =

��

c) trobeu l’equació del pla que passa per B, C i D; Podem trobar l’equació del pla a partir d’un punt i dos vectors.

( ) ( ) ( )0,0,2 0,0,0 0,0,2AB B A= − = − =��



( ) ( ) ( )0,2,0 0,0,2 0,2, 2BC C B= − = − = −��

( ) ( ) ( )2,0,0 0,0,2 2,0, 2BD D B= − = − = −��

Finalment l’equació general del pla π que passa pel punt ( )0,0,2B= i té com a vectors

directors ( )0,2, 2BC = −��

i ( )2,0, 2BD = −��

és:

( ) ( )4

0 0 2

: 0 2 0 0 4 4 4 2 0 2 0

2 2 2

x

y x y z x y z

z

π ÷ −

−− = → − − − − = → + + − =− − −

d) calculeu la distància de l’origen al pla de l’apartat anterior.

Sabem que donat un punt ( )1 2 3, ,P p p p= i un pla : 0Ax By Cz Dπ + + + = podem calcular

la distància entre el punt i el pla com: . En el nostre cas:

( )0,0,0P= , : 2 0x y zπ + + − = i ( )2 2 2

0 0 0 2 2 2 2 3,

33 31 1 1d P π

+ + − −= = = =

+ +

27) PAU LOGSE 2004 Sèrie 4 Qüestió 1: Considereu els punts de l’espai A(1, 1, 2), B(0, 1, 1) i C(k, 1, 5). a) Trobeu l’equació de la recta que passa per A i B.

( ) ( ) ( )0,1,1 1,1,2 1,0, 1AB B A= − = − = − −��

proporcional a ( )1,0,1v =�

Finalment la recta que passa per A i per B serà la recta que passa pel punt ( )1,1,2A= amb

vector director ( )1,0,1v =� , és a dir: ( ) ( ) ( ): , , 1,1,2 1,0,1r x y z λ= +

Altres equacions de la recta r serien:

Equacions continues: 1 1 2

:1 0 1

x y zr

− − −= =

( ) ( )( ) ( )

0 1 1 1 1 0 11 1 2: :

1 2 11 0 1 1 1 1 2

x y y yx y zr r

x z x zx z

⋅ − = ⋅ − − = = − − − = = → → → − = − − = −⋅ − = ⋅ −

b) Per a quins valors de k els punts A, B i C formen un triangle? Tres punts formen triangle sii no estan alineats, és a dir, tres punts A, B i C formen triangle sii

els vectors AB��

i AC��

són proporcionals.

Estudiem dons la proporcionalitat o no dels vectors AB��

i AC��

.

( ) ( ) ( )0,1,1 1,1,2 1,0, 1AB B A= − = − = − −��

( ) ( ) ( ),1,5 1,1,2 1,0,3AC C A k k= − = − = −��

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +



( )1,0, 1AB= − −��

i ( )1,0,3AC k= −��

proporcionals sii

( )1 0 31 1 1 3 1 3 4

1 0 1

kk k k

− = = → − ⋅ − = − ⋅ → − = → =− −

Per tant, donat que els tres punts A, B i C estan alineats sii 4k = podem afirmar que aquestos

tres punts formaran triangle sii 4k ≠ 28) PAU LOGSE 2004 Sèrie 4 Problema 2:

Considereu la recta r d’equació

3 2

5 2

3

x t

y t

z t

= − + = − = +

i el punt M (2, 3, 7).

a) Trobeu, en funció de t, la distància de M a un punt qualsevol de la recta r.

Qualsevol punt P de la recta r serà de la forma

La distància entre els punts P i M serà el mòdul del vector que formen.

( ) ( ) ( )3 2 , 5 2 , 3 2,3,7 5 2 , 2 2 , 4MP P M t t t t t t= − = − + − + − = − + − − +��

Finalment:

( ) ( ) ( ) ( ) ( )2 2 2, 5 2 , 2 2 , 4 5 2 2 2 4d M P MP t t t t t t= = − + − − + = − + + − + − + =

��

2 2 2 225 20 4 4 8 4 16 8 9 36 45t t t t t t t t= − + + − + + − + = − + =

( )2 29 4 5 3 4 5t t t t= − + = − +

b) Trobeu les coordenades dels punts A i B de r situats a distància 3 2 del punt M.

( ), 3 2 3d P M = → 2 4 5 3t t− + = 22 4 5 2t t→ − + = →

2 2 14 5 2 4 3 0

3

tt t t t

t

=→ − + = → − + = → =

Substituint en l’expressió del punt P : tenim que:

Per tant:

Quan 1t = tenim: ( ) ( )3 2 1, 5 2 1, 3 1 1,3,4A A= − + ⋅ − ⋅ + → = −

I quan 3t = : ( ) ( )3 2 3, 5 2 3, 3 3 3, 1,6B B= − + ⋅ − ⋅ + → = −

c) El triangle AMB, és rectangle en M?

Tenim que ( )2,3,7M = , ( )1,3,4A= − i ( )3, 1,6B= −

El triangle AMB serà rectangle en M sii els vectors MA��

i són ortogonals. És a dir, si el seu producte escalar és zero. Anem a comprovar aquesta última condició.

( ) ( ) ( )1,3,4 2,3,7 3,0, 3MA A M= − = − − = − −��

( ) ( ) ( )3, 1,6 2,3,7 1, 4, 1MB B M= − = − − = − −��

( )3 2 , 5 2 , 3P t t t= − + − +

( )3 2 , 5 2 , 3P t t t= − + − +

MB��



( ) ( )3,0, 3 1, 4, 1 3 0 3 0MA MB⋅ = − − ⋅ − − = − + + =��

per tant el triangle AMB és rectangle en

M. d) Els punts A i B formen part d’un paral·lelogram de vèrtexs ABCD que té el centre de simetria en el punt M. Calculeu les coordenades de C i D. Evidentment, abans de començar necessitem un dibuix de la situació. Podem observar que el punt C es pot calcular com:

Anàlogament:

( ) ( ) ( )2,3,7 1,4,1 1,7,8D M BM= + = + − =��


Considereu les rectes 2 1

:2 1 2

x y zr

− += =− −

i

1 3

: 1 4

5

x t

s y t

z t

= + = − − = +

a) Estudieu la seva posició relativa. De les equacions de les rectes podem extreure que:

( )2,1, 2rv = − −�, ( )3, 4,1sv = −�

( )2, 1,0A r= − ∈ i

Evidentment rv�

i sv�

no proporcionals. Per tant, les rectes r i s no poden ser ni paral·leles ni

coincidents. Així r i s o bé són secants en un punt o bé es creuen. Per saber en quin dels dos casos ens trobem utilitzarem un argument que ha sortit diversos cops durant el curs. És el següent: Si les dues rectes r i s es tallen en un punt aleshores els

vectors rv�

, sv�

i el vector AB��

són coplanaris i per tant la matriu que es forma amb tots 3 té

rang 2 mentre que si les rectes r i s es creuen aleshores aquestos vectors no són coplanaris i per tant aquesta matriu té rang 3.

( ) ( ) ( )1, 1,5 2, 1,0 1,0,5AB B A= − = − − − = −��

2 3 1

, , 1 4 0 32 0

2 1 5r sv v AB

− −= − = ≠ →

−

�� r i s es creuen.

b) Trobeu l’equació del pla que conté s i és paral·lel a r. El pla π que conté a la recta s i és paral·lel a la recta r té com a vectors directors els dos

vectors de les dues rectes ( )r sv i v� �

i per contenir a la recta s també podem assegurar que

aquest pla passa pel punt . Així:

( )2,1, 2rv = − −� i ( )3, 4,1sv = −�

vectors directors de π i ( )1, 1,5B s= − ∈ . Per tant:

( ) ( ) ( )2,3,7 3,0,3 5,3,10C M AM= + = + =��

( )1, 1,5B s= − ∈

( )1, 1,5B s= − ∈



( ) ( ) ( ) ( ) ( ) ( )1 2 3

: 1 1 4 0 1 6 1 8 5 3 5 8 1 2 1 0

5 2 1

x

y x y z z x y

z

π− −+ − = → − − + + − − − − − + + = →− −

( ) ( ) ( )7 1 4 1 5 5 0 7 7 4 4 5 25 0x y z x y z→ − − − + + − = → − + − − + − = →

: 7 4 5 22 0 : 7 4 5 22 0x y z x y zπ π→ − − + − = → + − + =

c) Calculeu la distància entre r i s. Podem calcular la distància entre dues rectes r i s que es creuen mitjançant la fórmula:

( ), ,

,r s

r s

v v ABd r s

v v

=

×

��

� � .

Cal notar que el numerador de la fracció anterior és el valor absolut del producte mixt dels

vectors rv�

, sv�

i AB��

que hem calculat en l’apartat a). Queda per calcular dons el

denominador.

( ) ( ) ( )2,1 2 3, 4,1 2 1 2 1 8 6 3 8 2 7, 4,5

3 4 1r s

i j k

v v i k j k i j× = − − × − = − − = + − − − + = − −−

��

� ��

Finalment:

( ) ( ) ( ) ( )2 2 2

, , 32 32 32,

7, 4,5 49 16 257 4 5

r s

r s

v v ABd r s

v v

= = = = =

× − − + +− + − +

��

� �

32 16 10

1590= =



:4 3 3

x y zr

− − += =−

i el pla :π 3x + 4y + 7 = 0.

Sabem que les posicions relatives entre una recta i un pla són: 1) Què la recta sigui secant al pla en un punt. 2) Que la recta i el pla siguin paral·lels. i 3) Que la recta estigui continguda en el pla. Al calcular la distància entre la recta i el pla tindrem que si la recta és secant al pla en un punt o la recta està continguda en el pla aleshores la distància entre recta i pla serà 0. Per tant, l’única possibilitat per a que la distància entre r i π sigui no nul·la és que r i π siguin paral·lels. Comencem dons estudiant la posició relativa entre la recta r i el pla π . Aquesta posició relativa la podem trobar per Rangs o també de la manera següent: Tal i com es pot observar en la figura adjunta si la recta r i el pla

π són paral·lels, aleshores el vector director de r , rv�

i el vector



normal de π , nπ�

són ortogonals. És a dir, el seu producte escalar ha de ser zero. Comprovem-

ho.

( ) ( )4, 3,3 3,4,0 12 12 0 0r rv n v nπ π⋅ = − ⋅ = − + = → ⊥� � � � i per tant la recta r o bé és paral·lela

al pla π o bé està continguda en aquest. Per sortir d’aquesta disjuntiva, agafem un punt de r i comprovem si pertany o no a π .

Sigui ( )3,1, 2P r= − ∈ , la pregunta és ¿ ?P π∈

Dons substituïm el punt P en l’equació de π i tenim: 3 3 4 1 7 9 4 7 20 0 P r iπ π⋅ + ⋅ + = + + = ≠ → ∉ → paral·lels. Finalment, una vegada comprovat que r i π són paral·lels, la distància entre la recta r i el pla π serà la de qualsevol punt P de r a π i es podrà calcular mitjançant la fórmula:

( )1 2 3, ,P p p p= i : 0Ax By Cz Dπ + + + = aleshores ( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +

En el nostre cas, agafant ( )3,1, 2P r= − ∈ i : 3 4 7 0x yπ + + = tenim que:

( )2 2 2

3 3 4 1 7 9 4 7 20 20, 4

5 5253 4 0d P π

⋅ + ⋅ + + += = = = =

+ +



:2 3 3

x y zr

− − += =−

i el pla π : 2x – 3y + 3z + 5 = 0.

Ja hem treballat en diferents ocasions i ho hem repetit en el problema anterior que abans de ficar-nos a calcular distàncies entre objectes cal estudiar la posició relativa perquè si aquestos objectes tenen algun punt en comú aleshores la distància serà zero. Per tant, el primer que hem de fer és estudiar la posició relativa entre la recta r i el pla π . Sempre tenim l’opció de calcular la posició relativa raonant per Rangs però en aquest cas hi ha un mètode molt més ràpid. És el següent: Podem observar que en aquest cas el vector director de la recta r ,

( )2, 3,3rv = −� i el vector normal al pla π , ( )2, 3 3nπ = − −�

coincideixen. Això voldrà dir, tal i com s’aprecia en la figura adjunta, que la recta r i el pla π són perpendiculars, per tant secants, i per tant la distància entre ells serà zero. 32) PAU LOGSE 2005 Sèrie 3 Qüestió 4: Donats els punts A = (1, 0, 0) i B (0, 0, 1):

a) Trobeu un punt C sobre la recta d’equació paramètrica

1

1

1

x

y

z

λλ

= = + = +

que faci que el triangle

ABC sigui rectangle en C.



El triangle ABC serà rectangle en C si els vectors CA��

i

CB��

són ortogonals. És a dir, si el seu producte escalar és zero. Com C és un punt de la recta, aleshores C tindrà la forma:

( )1, 1 , 1C λ λ= + + i per tant els vectors CA��

i CB��

seran:

( ) ( ) ( )1,0,0 1, 1 , 1 0, 1 , 1CA A C λ λ λ λ= − = − + + = − − − −��

( ) ( ) ( )0,0,1 1, 1 , 1 1, 1 ,CB B C λ λ λ λ= − = − + + = − − − −��

( ) ( )0 0, 1 , 1 1, 1 , 0CA CB λ λ λ λ⋅ = → − − − − ⋅ − − − − = →��

( ) ( ) ( ) ( ) 2 20 1 1 1 0 1 2 0λ λ λ λ λ λ λ λ→ + − − ⋅ − − + − − ⋅ − = → + + + + = →

2

12 3 1 0 1

2

λλ λ

λ

= −→ + + = → −=

Per tant, en aquest cas APARENTMENT, hi ha dos punts que compleixen el requisit que són:

• Quan 1λ = − aleshores ( ) ( )1,1 1,1 1 1,0,0C = − − = que és igual al punt A i per tant en

aquest cas els punts A, B i C no formen triangle.

• Quan 1

2λ −= aleshores

1 1 1 11,1 ,1 1, ,

2 2 2 2C

= − − =

diferent de A i de B, per tant, en

aquest cas els punts A, B i C si que formen triangle.

Així la solució al problema és 1 1

1, ,2 2

C =

b) Trobeu l’àrea del triangle ABC. Donat que el triangle ABC és rectangle en C tenim que els catets CA i CB formen 90º (és a dir, són ortogonals) i per tant els podem utilitzar com a base i com a altura. Per tant:

( ) 1 1 1 11,0,0 1, , 0, ,

2 2 2 2CA A C

− − = − = − = →

��

2 22 1 1 1 1 2 2

0 02 2 4 4 4 2

CA− − → = + + == + + = =

��

( ) ( )2 2

21 1 1 1 1 10,0,1 1, , 1, , 1

2 2 2 2 2 2CB B C CB

− − = − = − = − → = − + + =

��

1 1 6 31

4 4 4 2= + + = =

Finalment:

2

2

Base x AlturaÀrea triangle= =

32 2

⋅ 32 3

2 2 4= = unitats d’àrea.



33) PAU LOGSE 2005 Sèrie 4 Problema 2: Una piràmide de base quadrada té el vèrtex en el pla d’equació z = 3. Tres dels vèrtexs de la base són els punts del pla OXY: A = (1, 0, 0), B = (1, 1, 0) i C = (0, 1, 0). a) Feu un gràfic dels elements del problema. Quines són les coordenades del quart vèrtex de la base, D? Si heu fet el dibuix bé s’aprecia clarament que el quart vèrtex de la base de la piràmide és l’origen de coordenades, és a dir, el punt

D és ( )0,0,0D =

b) Quin és el volum de la piràmide? 3

àrea base alturaVolum

× =

La base és un quadrat de costat 1, per tant, l’àrea de la base és 1 1 1A= ⋅ = . L’altura de la piràmide és la distància entre els plans OXY (d’equació 0z = ) i el pla 3z = , per tant, l’altura

és 3. Finalment el volum de la piràmide serà: 31 31

3 3

àrea base alturaVolum u

× ×= = =

c) Si el vèrtex de la piràmide és el punt V = (a, b, 3), quina és l’equació de la recta que conté l’altura sobre la base? Del vèrtex de la piràmide solament ens diuen que està en el pla 3z = , per tant, aquest vèrtex

serà un punt de la forma ( ), ,3V a b= on no podem precisar ni

a ni b. L’altura de la piràmide és el segment perpendicular a la base, és

a dir, al pla 0z = i que passa pel vèrtex ( ), ,3V a b= . Per tant,

la recta que conté a l’altura sobre la base serà la recta

perpendicular al pla 0z = i que passa pel punt ( ), ,3V a b=

(en vermell). Però si una recta r és perpendicular a un pla π , aleshores el vector director de la recta coincideix amb el vector normal del pla, és a dir, rv nπ=� �

.

Però ( ) ( ): 0 0,0,1 0,0,1z n nπ ππ = → = → =� �.

Així la recta r és la recta que passa pel punt ( ), ,3V a b= amb vector director ( )0,0,1rv =� i

en conseqüència tindrà les següents equacions:

• Equació vectorial: ( ) ( ) ( ): , , , ,3 0,0,1r x y z a b λ= +

• Equació continua: 3

:0 0 1

x a y b zr

− − −= =

• Equacions generals:



( ) ( )( ) ( )

1 0 3 03: :

00 0 1 1 0 3

x a z x a x ax a y b zr r

y b y by b z

⋅ − = ⋅ − − = = − − − = = → → → − = =⋅ − = ⋅ −

34) PAU LOGSE 2006 Sèrie 1 Qüestió 1: Trobeu les coordenades dels punts situats sobre la recta d’equació

que estan a distància 1 del pla 2 2 5x y z+ + = .

Sabem que la distància entre un punt ( )1 2 3, ,P p p p= i un pla

: 0Ax By Cz Dπ + + + = es pot calcular mitjançant la fórmula:

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +.

En el nostre cas, els punts de la recta

( ) ( ) ( ): , , 1,1,1 1,2,1r x y z t= − + tindran la forma

( )1 , 1 2 , 1P t t t= − + + + i per tant la distància entre aquest punt i el pla

: 2 2 5 0x y zπ + + − = serà:

( ) ( ) ( ) ( )1 2 3

2 2 2 2 2 2

2 1 2 1 2 1 5,

2 2 1

t t tAp Bp Cp Dd P

A B Cπ

− + + + + + −+ + += = =

+ + + +

2 2 2 4 1 5 7 4

39

t t t t− + + + + + − −= =

( )1

7 4 37 4, 1 1 7 4 3 7 4 3 1

7 4 337

ttt

d P t tt t

π=− =− = → = → − = → − = ± → → − = − =

Per tant els dos punts de la recta que estan a distància 1 del pla són:

( ) ( ) ( ) ( ) ( ) ( ) ( )1, , 1,1,1 1,2,1 , , 1,1,1 1,2,1 0,3,2tx y z t x y z== − + → = − + =

( ) ( ) ( ) ( ) ( ) ( ) ( )17 6 9 81 2 1

7 7 7 7 7 7, , 1,1,1 1,2,1 , , 1,1,1 , , , ,tx y z t x y z= −= − + → = − + =

Com es pot veure en el gràfic que acompanya a aquest problema hi haurà dos punts de la recta r que distaran 1 del pla π , un per sobre i l’altre per sota de π . (Són els que estan pintats de vermell) 35) PAU LOGSE 2006 Sèrie 1 Problema 1: Una recta r passa pel punt A = (3,0,2) i té la direcció del vector (–1,1,4). a) Trobeu quin angle forma r amb el pla horitzontal. L’angle que formarà la recta r i el pla horitzontal XY serà l’angle que forma el vector director

de la recta ( )1,1,4rv = −� amb el pla XY.

En la figura adjunta es veu que el pla horitzontal (pintat de groc) és el pla que conté tots els punts de coordenada z (altura)

( ) ( ) ( ), , 1,1,1 1,2,1x y z t= − +



igual a zero. Per tant, l’equació general del pla horitzontal és: 0z = . Recordem que l’angle entre una recta r de vector director rv

� i un pla π de vector normal nπ

�

es pot calcular mitjançant la fórmula: ( ), arcsin r

r

v nr

v nπ

π

π ⋅

= ⋅

� �

∡ � �

En el nostre cas: ( )1,1,4rv = −�, ( )0,0,1nπ =�

( ) ( )1,1,4 0,0,1 4rv nπ⋅ = − ⋅ =� �

( ) ( )2 2 21,1,4 1 1 4 18rv = − = − + + =� i ( ) 2 2 20,0,1 0 0 1 1 1nπ = = + + = =�

( ) 4 4, arcsin arcsin arcsin 70,53º

18 1 18r

r

v nr

v nπ

π

π ⋅ = = = ⋅ ⋅

� �

∡ ≃� �

b) Comproveu que no passa pel punt B = (1,3,10).

Per comprovar que la recta r no passa pel punt ( )1,3,10B = serà

suficient demostrar que aquest punt B no compleix les equacions

de ( ) ( ) ( ): , , 3,0,2 1,1,4r x y z λ= + − però hi ha una manera més

ràpida. És la següent:

Sabem que ( )3,0,2A= és un punt de la recta r . Si ( )1,3,10B =

fos un altre punt de r aleshores el vector AB��

hauria de ser proporcional al vector director de

la recta r que és ( )1,1,4rv = −�. (Mirar figura adjunta)

( ) ( ) ( )1,3,10 3,0,2 2,3,8AB B A= − = − = −��

AB��

i rv�

proporcionals sii 2 3 8

1 1 4

− = =−

que òbviament és fals donat que la primera fracció

dóna 2 mentre que la segona dóna 3 i per tant el punt B no és de la recta r . Un altra manera que podríem dir tradicional de demostrar que el punt B no és un punt de r és substituir-lo en l’equació de r i comprovar que dóna una contradicció, en aquest cas

tindríem: ( )1,3,10B = i ( ) ( ) ( ): , , 3,0,2 1,1,4r x y z λ= + − aleshores:

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )1,3,10 3,0,2 1,1,4 1,3,10 3,0,2 1,1,4 2,3,8 1,1,4λ λ λ= + − → − = − → − = − →2 2

3 3

8 4

λ λλ λ

λ

− = − → =→ = → = =

que és una contradicció donat que λ no pot valer simultàniament 2 i

3. c) Trobeu l’equació de la recta que passa per A i B.



( )3,0,2A= , ( )1,3,10B = ( ) ( ) ( )1,3,10 3,0,2 2,3,8AB B A= − = − = −��

per tant, la recta

que passa per A i per B es pot escriure com: ( ) ( ) ( ): , , 3,0,2 2,3,8s x y z λ= + −


Determineu l’equació del pla perpendicular a la recta 1 0

:2 0

x yr

x z

− − = + + =

que passa pel punt

(1,1,2). Quina distància hi ha d’aquest pla a l’origen de coordenades? Anomenem π al pla que busquem. Si el pla π és perpendicular a la

recta r , aleshores el vector normal a π , nπ�

serà el vector director de la

recta r , rv�

tal i com es pot observar en el dibuix.

Per tant, necessitem calcular el vector director de 1 0

:2 0

x yr

x z

− − = + + =

.

Recordem que quan una recta bé donada com a intersecció de dos plans (com ara) el vector director de la recta és el producte vectorial dels vectors normals d’aquests plans. En el nostre cas:

( ) ( ) ( )1 0: 1, 1,0 1,0,1 1 1 0 1, 1,1

2 01 0 1

r

i j kx y

r v i k jx z

− − =→ = − × = − = − + − = − − + + =

��

��

Per tant, ( ) ( )1,1,21, 1,1 : 0 1 1 2 0Prn v x y z D Dπ

π π = ∈= = − − → − − + + = →− − + + = →� �

0 : 0 : 0D x y z x y zπ π→ = → − − + = → + − =

Quina distància hi ha d’aquest pla a l’origen de coordenades?

( )0,0,0O π= ∈ perquè compleix l’equació de π , per tant, ( ), 0d O π =

NOTA: Un altra manera d’aconseguir el vector director de la recta r i per tant el vector normal al pla π seria trobar l’equació vectorial de la recta r a partir de les seves equacions generals aïllant dues incògnites en funció de l’altra. El raonament seria:

1 0 1 2 1 3:

2 0 2 2 2zx y x y y y

rx z x x x

λ λ λλ λ λ

=− − = − = − − − = = − − → → → → + + = = − − = − − = − −

( ) ( ) ( ) ( ) ( ) ( ), , 2 , 3 , , , 2, 3,0 1, 1,1 1, 1,1rx y z x y z vλ λ λ λ→ = − − − − → = − − + − − → = − −�



:3 2 0

x y zr

x y z

− − − = − − − =

i el pla π : 2x – y + az + 2 = 0 on a és un

paràmetre. a) Trobeu un vector director de la recta i un vector perpendicular al pla.



A l’igual que abans per trobar el vector director d’una recta que ve donada mitjançant les seves equacions generals, és a dir, com a intersecció de dos plans 'π i ''π . És suficient calcular el producte vectorial dels vectors normals a aquestos plans. En el nostre cas:

( )( )

'

' ''

''

2, 5, 1' : 2 5 3 0' ''

'' : 3 2 0 1, 3, 1r

nx y zr on v n n

x y z n

ππ π

π

ππ π

π= − −− − − = = ∩ → → = × = − − − = = − −

��

�

( ) ( ) ( )2, 5, 1 1, 3, 1 2 5 1 5 6 5 3 2 2 2,1, 1

1 3 1

i j k

i k j k i j i j k= − − × − − = − − = − − + − + = + − = −− −

��

� � ��

Per tant, el vector director de la recta r és ( )2,1, 1rv = −�

NOTA: No cal dir que també podem trobar el vector director de la recta r calculant la seva equació vectorial a partir de les generals. En aquest cas el que hem de fer és anomenar λ a una de les tres incògnites x , y o z i ficar les altres dues en funció de λ . En el nostre cas

seria: 2 5 3 0 2 5 3 0 2 3 5

:3 2 0 3 2 0 2 3

yx y z x z x zr

x y z x z x zλ λ λ

λ λ=− − − = − − − = − = +

→ → − − − = − − − = − = +

Restant les dues equacions tenim que: 1 2x λ= + Finalment substituint x en la segona equació:

2 3 1 2 2 3 1 2 2 3 1x z z z zλ λ λ λ λ λ− = + → + − = + → = + − − → = − − Per tant:

( ) ( ) ( ) ( ) ( ) ( ), , 1 2 , , 1 : , , 1,0, 1 2,1, 1 2,1, 1rx y z r x y z vλ λ λ λ= + − − → = − + − → = −�

Per altra banda, el vector normal al pla : 2 2 0x y azπ − + + = és ( )2, 1,n aπ = −�

b) Quin ha de ser el valor de a per tal que la recta i el pla siguin paral·lels? Cal notar que per saber si la recta r i el pla π són paral·lels o no podem treballar amb les seves posicions relatives mitjançant els rangs de la matriu de coeficients i la matriu ampliada però podem utilitzar un altre procediment que serà substancialment més ràpid perquè utilitza els resultats de l’apartat anterior. És el següent: Si la recta r , i el pla π són paral·lels, aleshores els vectors rv

� i

nπ�

han de ser ortogonals. És a dir, el seu producte escalar ha de

donar zero. Anem a imposar aquesta condició.

( ) ( )0 2,1, 1 2, 1, 0 4 1 0 3 0 3rv n a a a aπ⋅ = → − ⋅ − = → − − = → − = → =� �

Aquí hem comès un petit error. Perquè imposar que el vector director de la recta i el vector normal al pla siguin perpendiculars no ens assegura que el pla i la recta siguin paral·lels perquè també podria passar que la recta estigués continguda dintre del pla. Per descartar aquesta possibilitat agafem un punt de la recta i mirarem que no compleix l’equació del pla. Sigui

( )1,0, 1P r= − ∈ al substituir en l’equació del pla quan 3a = tenim que:



( ) ( )1,0, 1: 2 3 2 0 2 1 0 3 1 2 1 0Px y z P rπ π= −− + + = → ⋅ − + ⋅ − + = ≠ → ∉ → no continguda

en el pla rπ π→ � . Per tant, aclarida esta observació ara si que podem assegurar que pel

valor del paràmetre 3a = la recta r i el pla π són paral·lels. c) Esbrineu si existeixen valors de a per als quals la recta i el pla siguin perpendiculars. En cas afirmatiu, calculeu-los. Basant-nos en el mateix dibuix que en l’apartat anterior girant la recta 90º podem veure que la recta r i el pla π són perpendiculars sii els vectors rv

� i nπ�

apunten en la mateixa direcció, és a dir, si són proporcionals. Anem dons a imposar aquesta condició:

rv�

i nπ�

proporcionals ( )2,1, 1→ − i ( )2, 1,a− proporcionals

2 1 1

2 1 a

−→ = =−

. Veiem que aquest cas és impossible dons la

primera fracció sempre val 1 mentre que la segona sempre val -1. d) Esbrineu si existeixen valors de a per als quals la recta i el pla formin un angle de 30º. En cas afirmatiu, calculeu-los. Sabem que per calcular l’angle agut que formen una recta de vector director rv

� i un pla de

vector normal nπ�

podem utilitzar la fórmula: sin r

r

v n

v nπ

π

α⋅

=⋅

� �

� � on α és l’angle buscat.

En el nostre cas:

( ) ( ) ( )( ) ( )

( )( ) ( )2 22 2 2 2

2,1, 1 2, 1, 2 2 1 1 11sin 30º

22,1, 1 2, 1, 2 1 1 2 1

a a

a a

− ⋅ − ⋅ + ⋅ − − ⋅= → = →

− ⋅ − + + − ⋅ + − +

2

2 2

4 1 31 16 5 2 3

2 24 1 1 4 1 6 5

a aa a

a a

− − −→ = → = → ⋅ + = −

+ + ⋅ + + ⋅ +

Però elevant al quadrat tenim que:


Calculeu l’equació de la recta paral·lela a la recta i que passa pel punt

(0,1,0). Anomenem a aquesta recta paral·lela. És evident que tindrà el mateix vector director que

i a més passarà pel punt .

Anem a calcular el vector director de . Per fer-ho tenim dos mètodes.

( ) ( ) ( ) ( ) ( )2 2 22 2 2 2 26 5 2 3 6 5 2 3 30 6 4 9 6a a a a a a a⋅ + = − → ⋅ + = − → + = − + →

22 2 2 230 6 36 24 4 2 24 6 0 12 3 0 6 39a a a a a a a a÷→ + = − + → + − = → + − = → = − ±

0:

2 1

x y zr

x y z

+ − = − + =

'r 'rr ( )0,1,0P =

r



• Mètode 1: El vector director d’una recta definida com a intersecció de dos plans és el producte vectorial dels vectors normals d’aquestos plans. En el nostre cas:

Finalment proporcional a

. Per tant, la recta buscada és:

• Mètode 2: Calculem l’equació vectorial de la recta a partir de les seves equacions generals.

Sumant les dues equacions tenim que:

Substituint en la primera equació així:

obtenint com

és obvi el mateix vector director que amb l’altre mètode.

Una vegada sabem que el vector director de és i que la recta passa pel punt

trobaríem l’equació vectorial de la recta igual que ho hem fet abans.

Per altra banda crec que la manera més ràpida de donar amb la recta que ens demanen és:

La recta es paral·lela a la recta per tant, la part vectorial de les

equacions de les rectes i serà la mateixa. És a dir, la recta serà de la forma

. Però com sabem que substituint en l’equació tenim que:

39) PAU LOGSE 2006 Sèrie 4 Qüestió 4: Determineu els extrems d’un segment AB sabent que el punt A pertany al pla ,

el punt B pertany a la recta i el punt mitjà del segment és .

En aquest cas, com en molts altres davant d’un problema geomètric el més important és fer un bon dibuix de la situació.

( )( )1,1, 10 : 0

: '2 1 ' : 2 1 ' 2, 1,1

nx y z x y zr r on

x y z x y z n

ππ π

π= −+ − = + − = → = ∩ → − + = − + = = −

�

�

( ) ( ) ( )' 1,1, 1 2, 1,1 1 1 1 0, 3, 3

2 1 1r

i j k

v n n= × = − × − = − = − −−

��

� � �

( )0,1,1v =� ( ) ( ) ( )' : , , 0,1,0 0,1,1r x y z λ= +r

0:

2 1 2 1zx y z x y

rx y z x y

λ λλ

=+ − = + = → − + = − = −

13 1

3x x= → =

1 1

3 3y yλ λ+ = → = −

( ) ( ) ( ) ( ) ( ) ( )1 1 1 13 3 3 3: , , , , : , , , ,0 0,1,1 0,1,1rr x y z r x y z vλ λ λ−= − → = + → =�

'r ( )0,1,1rv =� 'r

( )0,1,0P = 'r

'r0

:2 1

x y zr

x y z

+ − = − + =

r 'r 'r

' :2

x y z ar

x y z b

+ − = − + =

( )0,1,0 'P r= ∈

2 2 10 1 0 1 1 1

' : ' : ' :2 0 1 0 1 2 1 3 0

F F Fa a x y z x y zr r r

b b x y z x→ ++ − = = + − = + − =

→ → → → ⋅ − + = = − − + = − =

1 0 1 1' : ' : ' :

3 0 0 0

x y z y z y zr r r

x x x

+ − = + − = − = → → → = = =

2 0x y z+ + =1 2

2 1 3

x y z− −= =−

( )0,0,0



Anomenem a l’origen de coordenades, és a dir . Sigui

l’extrem del segment que pertany al pla .

Donat que és el punt mitjà del segment tenim que els vectors i són iguals.

És a dir .

Però

Tenim dons que:

Per tant, imposant que és el punt mitjà del segment hem arribat a la

conclusió de que si aleshores . (En realitat això era obvi

perquè era el simètric de respecte de l’origen de coordenades i per tant les coordenades dels punts i són les mateixes però canviades de signe)

Finalment imposem que i que .

Si ajuntem la primera equació amb les altres dues tenim el sistema:

que té com a solució

Per tant la resposta al problema és:

i

40) PAU LOGSE 2007 Sèrie 1 Qüestió 2: Considereu els punts de l’espai P = (–1, a – 1, 3), Q = (0, a – 2, 1 – a) i R = (2, –1, 6 – 6a). a) Trobeu el valor de a per al qual els tres punts estan alineats.

Els punts P, Q i R estaran alineats sii els vectors i

O ( )0,0,0O = ( )1 2 3, ,A p p p=

AB π

O AB OA��

BO��

OA BO=��

( ) ( ) ( )1 2 3 1 2 3, , 0,0,0 , ,OA A O p p p p p p= − = − =��

( ) ( ) ( )1 2 3 1 2 3

1 2 3

, , , ,, ,

OA BOBO p p p O B p p p

OA p p p

= → = → − = →=

��

( ) ( ) ( ) ( ) ( )1 2 3 1 2 3 1 2 30,0,0 , , 0,0,0 , , , ,B p p p B p p p p p p→ − = → = − = − − −

( )0,0,0O = AB

( )1 2 3, ,A p p p= ( )1 2 3, ,B p p p= − − −B A

A B

: 2 0A x y zπ∈ + + =1 2

:2 1 3

x y zB r

− −∈ = =−

( )1 2 3 1 2 3, , : 2 0 2 0A p p p x y z p p pπ= ∈ + + = → + + =

( ) 31 21 2 3

1 21 2, , :

2 1 3 2 1 3

pp px y zB p p p r

−− − − −− −= − − − ∈ = = → = = →− −

1 2 1 2

1 3 1 3

1 2 4 2 5

3 3 2 3 2 3

p p p p

p p p p

+ = − − + = − → → + = − = −

1 2 3

1 2

1 3

2 0

2 5

3 2 3

p p p

p p

p p

+ + = + = − − = −

( ) ( )811 2 3 3 3, , , ,2p p p −=

( ) ( )811 2 3 3 3, , , , 2A p p p −= = ( ) ( )81

1 2 3 3 3, , , , 2B p p p −= − − − = −

PQ��

PR��

( ) ( ) ( )0, 2, 1 1, 1, 3 1, 1, 2PQ Q P a a a a= − = − − − − − = − − −��



i proporcionals sii

Per tant, la solució del problema és

b) Quan els tres punts estan alineats, quina és l’equació de la recta que els conté? Per saber la recta necessitem un punt i un vector director:

Punt:

Vector director:

Per tant, l’equació vectorial de la recta és:

41) PAU LOGSE 2007 Sèrie 1 Qüestió 4: Trobeu l’equació de la recta continguda en el pla , que talla els eixos OY i OZ. La part més difícil d’aquest problema és imaginar-se que cal fer. En la figura de l’esquerra tenim un pla i els eixos de coordenades dibuixats. En la següent figura dibuixo en color vermell intermitent la recta que estarà continguda en el pla

i que tallarà l’eix OY en un punt A i l’eix OZ en un punt B. Una vegada imaginada la situació, resulta evident que la recta

quedarà determinada pels punts A i B. Per tant, el problema queda resolt si trobo els punts A i B. Però això és força fàcil perquè el punt A és la intersecció del pla

amb l’eix OY i el punt B és la intersecció del pla amb l’eix OZ. Càlcul del punt A: Recordant que els punts de l’eix OY són els que tenen coordenades x i z igual a 0 tenim que:

Anàlogament, donat que els punts de l’eix OZ són els que tenen coordenades x i y igual a 0 tenim que:

( ) ( ) ( )2, 1, 6 6 1, 1, 3 3, , 3 6PR R P a a a a= − = − − − − − = − −��

PQ��

PR�� 1 1 2

3 3 6

a

a a

− − −= = →− −

1 13

213 3 6

3 3

3 6 3 6 9 3 3a

aa

a a

a a a a

−−

− −−

= → − = − → =→ = → − = − − → = → =

3a =

( ) ( ) ( )31, 1,3 1,3 1,3 1,2,3aP a P P== − − → = − − → = −

( ) ( )31, 1, 2 1, 1, 5aPQ a PQ== − − − → = − −��

( ) ( ) ( ): , , 1, 2,3 1, 1, 5r x y z λ= − + − −

: 2 6 2 0x y zπ + + − =

π

rπ

r

π π

2 6 2 0 0 2 6 0 2 0 0

0 0 1

0 0 0

x y z y x

A OY x x y

z z z

π+ + − = + + ⋅ − = =

= ∩ → = → = → = → = = =

( )0,1,0A =



Finalment calculem l’equació de la recta que passa pels punts A i B:

Vector director:

Hi ha un altre mètode molt més ràpid per calcular l’equació de la recta . En el segon dibuix, es veu que la recta , pel fet de tallar els eixos OY i OZ estarà continguda en el pla YZ. Per tant, la recta , per una banda estarà continguda en el pla de l’enunciat

i per l’altra en el pla YZ que té com a equació .

Finalment podem expressar la recta com la intersecció d’aquestos dos plans. És a dir:


Considereu la recta d’equació .

a) Expresseu el quadrat de la distància d’un punt qualsevol (x, y, z) de la recta al punt P = (1, 2, 5) com una funció de la coordenada x. D’entrada anem a expressar les coordenades y i z de qualsevol punt de la recta en funció de la coordenada x.

Per tant, un punt genèric de la recta es pot expressar com

Ara, la distància entre el punt de la recta i el punt serà el mòdul del vector

que formen.

Per tant, la solució a aquest apartat és:

b) Trobeu quin valor de x fa mínima aquesta funció, deduïu quin punt Q de la recta és el més proper a P i calculeu la distància del punt a la recta.

Hem de minimitzar la funció .

Per fer-ho igualem a zero la primera derivada.

13

2 6 2 0 0 2 0 6 2 0 0

0 0 0

0 0

x y z z x

B OY x x y

y y z

π+ + − = + ⋅ + − = =

= ∩ → = → = → = → = = =

( )130,0,B =

( ) ( ) ( )1 13 30,0, 0,1,0 0, 1,AB B A= − = − = −

��

( ) ( ) ( )13: , , 0,1,0 0, 1,r x y z λ= + −

rr

r: 2 6 2 0x y zπ + + − = 0x =

r

22 6 2 0 2 6 2 0 3 1 0: : :

0 0 0

x y z y z y zr YZ r r r

x x xπ ÷+ + − = + − = + − =

= ∩ → → → = = =

2 1:

2 2

y zr x

− −= =

r

2 2 2 22 1:

2 1 2 12 2

x y y xy zr x

x z z x

= − = + − −= = → → = − = +

r ( ), 2 2, 2 1rP x x x= + +

rP r ( )1,2,5P =

( ) ( ) ( ), 2 2, 2 1 1,2,5 1, 2 , 2 4r rPP P P x x x x x x= − = + + − = − −��

( ) ( )( ) ( ) ( ) ( )( )22 2 2 22 , 1, 2 , 2 4 1 2 2 4rd P P x x x x x x= − − = − + + − =

( ) ( ) ( )2 2 2 2 2 2 21 2 2 4 2 1 4 4 16 16 9 18 17x x x x x x x x x x= − + + − = − + + + − + = − +

( )2 2, 9 18 17rd P P x x= − +

( ) 29 18 17f x x x= − +



és un mínim relatiu de la funció.

Recordem que un punt genèric de la recta era i ara sabem que de

tots els punts de la recta el punt que minimitza la distància (o el quadrat de la distància)

al punt és el que s’obté pel valor , és a dir:

Finalment ens demanen la distància entre el punt i la recta . Però per construcció, aquesta distància és la distància entre els punts i .

,

c) Escriviu l’equació de la recta que passa per P i Q i comproveu que és perpendicular a r.

Per calcular la recta que passa pels punts P i Q necessitem el vector . Aquest l’hem

calculat en l’apartat anterior i és: proporcional a .

Així la recta passa pel punt i amb vector director , per tant:

Finalment ens queda per comprovar que les rectes i són perpendiculars. Però i perpendiculars sii el producte escalar dels seus vectors directors és zero. Comprovem-ho.

per tant .


Trobeu l’equació del pla perpendicular a la recta que passa per l’origen de

coordenades. Anomenem al pla que estem buscant.

( ) ( )29 18 17 ' 18 18f x x x f x x= − + → = −

( )' 0 18 18 0 18 18 1f x x x x= → − = → = → =

( ) ( )'' 18 '' 1 18 0 1f x f x= → = > → =r ( ), 2 2, 2 1rP x x x= + +

r Q

( )1,2,5P = 1x = ( ) 1, 2 2, 2 1 xrP x x x == + + →

( )1,4,3Q→ =

P r

P Q

( )1,2,5P = ( )1,4,3Q =

( ) ( ) ( )1,4,3 1,2,5 0,2, 2PQ Q P= − = − = −��

( ) ( ) ( ) ( )22 2, , 0,2, 2 0 2 2 8 2 2d P r d P Q PQ= = = − = + + − = =��

'r PQ��

( )0,2, 2PQ= −��

( )' 0,1, 1v = −

'r ( )1,2,5P = ( )' 0,1, 1v = −

( ) ( ) ( )' : , , 1,2,5 0,1, 1r x y z λ= + −

r 'rr 'r

( ) ( ) ( )' 1,2,2 0,1, 1 1 0 2 1 2 1 0 2 2 0v v⋅ = ⋅ − = ⋅ + ⋅ + ⋅ − = + − =� �'r r⊥

1

2 3

x y z

x y

+ + = + =

πrr n vππ ⊥ → =� �

( )3 21 1 3 2

:3 2 12 3 2 3 2

xyx y z y z y

rzx y y z

λ λλ λλ λλ λ

= = −+ + = + + = = − → → → → + − + =+ = + = = − +

( ) ( ) ( ) ( ) ( ) ( ): , , ,3 2 , 2 : , , 0,3, 2 1, 2,1 1, 2,1rr x y z r x y z vλ λ λ λ= − − + → = − + − → = −�

( ) ( )0,0,01, 2,1 : 2 0 0 : 2 0rn v x y z D D x y zππ π π∈= = − → − + + = → = → − + =� �



44) PAU LOGSE 2007 Sèrie 2 Qüestió 4: Trobeu els punts de la recta que equidisten dels plans

i .

El que farem serà primer ficar un punt genèric de la recta en funció d’un paràmetre. (Per exemple en funció de la seva coordenada ). Desprès calcularem les distàncies d’aquest punt als plans i .

Sabem que la distància entre un punt i un pla es

pot calcular mitjançant la fórmula: .

En el nostre cas, , i :

45) PAU LOGSE 2007 Sèrie 2 Problema 2: A l’espai es consideren els tres plans d’equacions:

, on p és un paràmetre real.

a) Esbrineu per a quins valors de p els tres plans es tallen en un únic punt. Trobeu aquest punt quan p = 1.

: 1 2r x y z− = + =

1 : 4 3 1 0x zπ − − = 2 : 3 4 1 0x yπ + − =

P r

z

1π 2π

( )1 1: 1 2 1, 2,

2 2

x z x zr x y z P z z z

y z y z

− = = + − = + = → → → = + − + = = −

( )1 2 3, ,P p p p= : 0Ax By Cz Dπ + + + =

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +( )1, 2,P z z z= + − 1 : 4 3 1 0x zπ − − = 2 : 3 4 1 0x yπ + − =

( ) ( )( )

1 22

4 1 3 1 4 4 3 1 3,

516 94 3

z z z z zd P π

+ − − + − − += = =

++ −

( ) ( ) ( )2 2 2

3 1 4 2 1 3 3 4 8 1 7 6,

59 163 4

z z z z zd P π

+ + − − + + − − −= = =

++

( ) ( ) ( )51 2

3 7 6, , 3 7 6 3 7 6

5 5xz z

d P d P z z z zπ π+ −

= → = → + = − → + = ± − →

9 36 9

3 7 6 6 23 7 6 3

8 38

z z zz z

z zz z

= → = → =+ = − → → + = − + = → =

( ) ( )32 5 31

2 2 21, 2, , ,zP z z z P= −= + − → =

( ) ( )38 13 311

8 8 81, 2, , ,zP z z z Q= −= + − → =

1 : 2 1x y zπ + + = 2 : 1px y pzπ + + = 3 : 2 1px y zπ + + =



Evidentment els tres plans es tallaran en únic punt si el sistema format per les seves equacions

és compatible determinat. És a dir, si .

El sistema és el següent:

Donat que la matriu de coeficients és una matriu quadrada, treballarem amb el seu determinant en detriment del mètode de Gauss. (Evidentment per Gauss el resultat seria el mateix)

Per tant, els únics valors del paràmetre que anul·len el determinant de la matriu són

i . Així, si aleshores

Però

els tres plans es tallen en un

únic punt.

Per tant, la resposta al problema és:

El problema també ens demana trobar el punt de tall quan .

Per tant, el punt de tall en aquest cas és:

b) Hi ha algun valor de p que faci que la intersecció comuna sigui una recta? Si és així, escriviu l’equació vectorial d’aquesta recta.

( ) ( )' º 3Rang M Rang M n incògnites= = =

2 1 1 2 1 1 1 2 1 1 2 1 1

1 1 1 1 ' 1 1

2 1 1 2 1 1 2 1 2 1

x y z

px y pz p p M p p i M p p

px y z p p p

+ + = + + = → → = = + + =

M

2 2

1 2 1 1 2 1

1 1 2 2 4 2 5 2

1 2 1 2

M p p M p p p p p p p p p

p p

= → = = + + − − − = − +

2

12

20 2 5 2 0

pM p p

p

== → − + = → =

p M

2p =1

2p = 1

2,2

p ∈ −

ℝ ( ) 3rang M =

( ) ( )3 ' º 3Rang M Rang M n incògnites= ≤ ≤ = →

( ) ( )' 3 º . . .Rang M Rang M n incògnites S C D→ = = = → →

12,

2p

∈ −

ℝ

1p =

2 2 1

3 3 1

1

1 2 1 1 1 2 1 1 1 2 1 1

' 1 1 ' 1 1 1 1 0 1 0 0

1 2 1 1 1 2 1 0 1 1 0

F F Fp

F F FM p p M

p

→ −=

→ −

= → = ≅ − − 0 0y y− = → =

00 0yy z z=− + = → =00

2 1 1yz

x y z x==+ + = → =

( )1,0,0P =



Sabem que si els tres plans es tallen en una recta aleshores el sistema és compatible indeterminat. Això fa que per a que els tres plans es tallen en una recta els rangs de les matrius

han de ser: .

Però per a que sigui 2 es necessita que . És a dir, si hi ha algun valor del

paràmetre per al qual els tres plans es tallen en una recta comuna aquest valor ha d’anul·lar

el determinant de la matriu i per tant, segons els càlculs de l’apartat a) solament hi ha dos

possibilitats. Que sigui o que sigui . Anem a estudiar per separat aquestos dos

casos: • Cas :

amb un grau de llibertat els tres plans es tallen en una recta. • Cas :

Podem observar que l’equació de la fila 2 és impossible, per tant, el sistema és incompatible i en aquest cas el que passa és que els tres plans mai es tallen a la vegada. És a dir, no tenen tots tres cap punt en comú. Per tant, l’únic valor del paràmetre que fa que els tres plans es

tallen en una recta és .

• Equació vectorial de la recta on es tallen els tres plans en el cas :

En el cas hem arribat a que el sistema és equivalent a que en forma

d’equacions seria

Per tant, el sistema format pels tres plans equival a la recta:

c) Trobeu quina és la posició relativa dels tres plans quan p = 1/2.

( ) ( )' 2Rang M Rang M= =

( )Rang M 0M =p

M

p 2 p1

2

2p =

2 2 122

1 2 1 1 1 2 1 11 2 1 1

' 1 1 ' 2 1 2 12 1 2 1

1 2 1 2 1 2 1

F F FpM p p M

p

→ −=

= → = ≅ ≅

( ) ( )2 2 12 1 2 1 1

' 2 3 º . . .0 3 0 1

F F F

Rang M Rang M n incògnites S C I→ −

≅ → = = < = → − − →

12p =

2 2 2 2 112

3 3 3 3 1

21 12 2 212

1 2 1 11 2 1 1 1 2 1 1

1 1' 1 1 ' 1 2 1 2

1 2 11 2 1 1 2 4 2

F F F F Fp

F F F F FM p p M

p

→ → −=

→ → −

= → = ≅ ≅

2 2 1

3 3 1

1 2 1 1

0 0 0 1

0 0 3 1

F F F

F F F

→ −

→ −

≅

p

2p =

2p =

2p =1 2 1 1

0 3 0 1

− −

1 1 13 3 3

1 1 13 3 3

2 1

3 1 2 1z

y y yx y z

y x z x z xλ

λ== = =+ + =

→ → → − = − + ⋅ + = + = = −

( ) ( ) ( ) ( ) ( )1 1 1 13 3 3 3: , , , , : , , , ,0 1,0,1r x y z r x y zλ λ λ= − → = + −



En l’apartat b) quan hem estudiat el cas hem arribat a la conclusió que el sistema

format pels tres plans era incompatible i per tant els tres plans no tenien cap punt en comú. A

partir de les matrius a les quals hem arribat també es veu que en aquest cas i

, per tant ja sabem que els tres plans no tenen cap punt en comú i que ens

trobem o bé en el cas 7 o bé en el cas 8 del llibre.

Cas 7 Cas 8

Els tres plans no tenen cap punt en comú i no

existeixen plans paral·lels Els tres plans no tenen cap punt en comú i hi

ha dos plans paral·lels Però quan el sistema que queda és:

d’on resulta evident multiplicant la segona fila per 2 que el pla

determinant per la primera fila i el pla determinat per la segona fila són paral·lels. Per tant,

estem en el cas 8, és a dir, quan els tres plans no tenen cap punt en comú i dos d’ells

són paral·lels secants al tercer. 46) PAU LOGSE 2007 Sèrie 3 Qüestió 1: Trobeu les equacions dels plans paral·lels a situats a 6 unitats de distància

d’aquest. Sabem que si un pla és paral·lel a , aleshores els dos plans tindran el mateix vector normal. És a dir, i per tant, donat que l’equació del pla és:

l’equació de serà de la forma .

Per tant, l’únic que necessitem és determinar el valor del paràmetre per a que la distància entre els plans i sigui 6 unitats. Però sabem que la distància entre dos plans paral·lels i

es pot calcular mitjançant la fórmula .

En el nostre cas:

1

2p =

( ) 2Rang M =

( )' 3Rang M =

12p =

1 12 2

12

1 2 1 1

1 1'

1 2 1

M

=

1

2p =

: 2 2 3x y zπ − + =

'π π'n nπ π=� � π : 2 2 3 0x y zπ − + − =

'π ' : 2 2 0x y z kπ − + + =k

: 2 2 3 0x y zπ − + − = ' : 2 2 0x y z kπ − + + =

: 0Ax By Cz Dπ + + + =

: ' 0Ax By Cz Dπ + + + = ( )2 2 2

', '

D Dd

A B Cπ π

−=

+ +

( )( )22 2

3 3 3, '

392 1 2

k k kd π π

− − − − − −= = =

+ − +



I per tant els dos plans situats a una distància de 6 unitats del pla de l’enunciat són:

i

Noteu que sempre hi haurà dos plans paral·lels situats a una determinada distància del pla donat, un per sobre i l’altre per sota. 47) PAU LOGSE 2007 Sèrie 3 Problema 1: Una recta r és paral·lela a la recta , talla en un punt A la recta

, i en un punt B la recta .

a) Trobeu l’equació del pla determinat per les rectes r i t. L’enunciat no ens dóna l’equació de la recta , però ens diu que és paral·lela a la recta . Per

tant, .

Per a que dues rectes r i t determinin un pla han de ser paral·leles (que no és el cas perquè

i no són proporcionals) o secants en un punt. Per tant, abans de

començar caldria comprovar que les rectes r i n són secants en un punt. Però això ja ens ho assegura l’enunciat quan diu que la recta r talla en un punt A la recta t. Per tant, una vegada feta la comprovació de rigor anem a buscar l’equació del pla que determinen les rectes r i t. Sabem que el pla contindrà les dues rectes r i t, per tant, els vectors directors d’aquestes

i seran també vectors directors del pla i qualsevol punt de les rectes pertanyerà a .

Agafant , i tenim que:

b) Trobeu el punt B calculant el punt d’intersecció del pla anterior amb la recta l. En aquest apartat ens demanen calcular el punt d’intersecció B entre el pla

de l’apartat anterior i la recta .

Per obtenir-lo solament necessitem resoldre el sistema format per l’equació general del pla i les dues equacions generals de la recta .

( ) 3 18 213, ' 6 6 3 18

3 18 153

k kkd k

k kπ π

− − = → = −− − = → = → − − = → − − = − → =

π

' : 2 2 15 0x y zπ − + + = '' : 2 2 21 0x y zπ − + − =

π

: 1 1 1s x y z− = − = −1

: 13 2

x yt z

− = = + 2 1:

2 2 3

x y zl

− −= =

r s

( )1,1,1r sv v= =� �

( )1,1,1rv =� ( )3,2,1tv =�

π

π rv�

tv� π

( )1,1,1rv =� ( )3,2,1tv =� ( )1,0, 1P t= − ∈

( )

1 1 3 1 1 3

: 0 1 2 0 1 2 0

1 1 1 1 1 1

x x

y y

z z

π− −− = → = →

− − +

( ) ( ) ( ) ( ) ( )1 3 2 1 3 1 2 1 0 1 2 1 0x y z z x y x y z→ − + + + − + − − − = → − − + − + = →

1 2 1 0 2 0 : 2 0x y z x y z x y zπ→ − + + − − = → − + − = → − + =

: 2 0x y zπ − + =2 1

:2 2 3

x y zl

− −= =

πl



Així el sistema queda:

c) Trobeu l’equació de la recta r. L’enunciat ens diu que la recta és paral·lela a la recta i que talla a la

recta en un punt .

Però i en l’apartat anterior hem calculat el punt que ens ha donat

.

Per tant la recta és la recta que passa pel punt i té com a vector director

. Per tant, la seva equació continua és:

d) Trobeu el punt A. Segons l’enunciat, el punt A és el punt d’intersecció entre les rectes i . Però ara, ja sabem les equacions d’aquestes dues rectes.

i

Per tant:

I el sistema format per les dues rectes serà:

De l’equació 3) tenim que .

Substituint en l’equació 4): .

( ) ( )( )

2 2 2 1 2 1 12 1:

3 3 2 3 2 32 2 3 3 1 2

x y x y x yx y zl

y z y zy z

− = − − = − − = − − = = → → → − = − =− =

3 3 22 2 1 32 0 1 2 1 0 1 2 1 0 1 2 1 0

1 1 1 0 1 0 1 1 1 0 1 1 1

3 2 3 0 3 2 3 0 3 2 3 0 0 1 0

F F FF F Fx y z

x y

y z

→ −→ −− + = − − −

− = → − ≅ − ≅ − − = − −

( ) ( ) ( )0 0 1 1 2 1 0 0 2 , , 2,1,0 2,1,0z y y x x x y z B= → − = → = → − ⋅ + = → = → = → =

r : 1 1 1s x y z− = − = −l B

( )1,1,1r sr s v v→ = =� �� B

( )2,1,0B =

r ( )2,1,0B =

( )1,1,1rv =�

2 1 0: : 2 1

1 1 1

x y zr r x y z

− − −= = → − = − =

r t

: 2 1r x y z− = − =1

: 13 2

x yt z

− = = +

2 2: 2 1

1 1

x z x zr x y z

y z y z

− = − = − = − = → → − = − =

( )( )

1 3 1 1 3 3 3 41: 1

2 2 2 23 2 2 1

x z x z x zx yt z

y z y zy z

− = + − = + − = − = = + → → → = + − == +

3 3 1

2 1 0 1 2 1 0 1 2

1 0 1 1 1 0 1 1 1

3 4 1 0 3 4 0 0 2 2

2 2 0 1 2 2 0 1 2 2

F F F

x z

y z

x z

y z

→ −

− = − − − = − − → ≅ − = − − − = − −

2 2 1z z− = → = −12 2 2 2 0zy z y y=−− = → + = → =



Substituint en l’equació 2): .

Substituint i en l’equació 1):

Per tant,

48) PAU LOGSE 2008 Sèrie 2 Qüestió 4: Trobeu l’equació de la recta perpendicular al pla , que passa pel punt

del pla.

Si una recta és perpendicular a un pla sabem que el vector

director de la recta serà el vector normal al pla . En el nostre

cas .

Per tant, per determinar la recta solament ens falta un punt.

L’enunciat ens diu que la recta passa pel punt i

que aquest punt és un punt del pla . Però si és un punt del pla , aleshores el punt complirà l’equació de , és a dir:

i per

tant:


Donades les rectes i i el punt ,

volem trobar l’equació de la recta que passa per P i que talla r i s. Per aconseguir-ho: a) Trobeu l’equació general o cartesiana (és a dir, l’equació de la forma Ax + By + Cz + D = 0) del pla que conté la recta r i el punt P.

Com el pla conté la recta aleshores, el vector director de també serà vector director de i el punt de també ho serà de

. Per altra banda, donat que els punts i seran punts del pla

podem assegurar que el vector serà vector director de .

Així el pla passa pel punt i té com a vectors directors i

, per tant:

11 1 1 0zy z y y=−− = → + = → =y z ( )12 1 2 1 2 1zx z x x x=−− = → − − = → + = → =

( )1,0, 1A = −

: 2 3 0x y zπ − + + =

( )1,3,a−

r πrv� π

( )2, 1,1rv nπ= = −� �

rr ( )1,3,P a= −

P πP π P

π( ) ( )2 1 3 3 0 2 3 3 0 2 0 2 1,3,2a a a a P⋅ − − + + = → − − + + = → − + = → = → = −

( ) ( ) ( ): , , 1,3, 2 2, 1,1r x y z k= − + −

2 1:

1 2 1

x y zr

− += =−

1 7 5:

1 2 3

x y zs

− + += = ( )1,1, 1P = −

π

( )( )1,2, 12 1

:1 2 1 2, 1,0

rvx y zr

Q r

= −− + = = → − = − ∈

�

π r rπ Q r

πP Q π

PQ��

π

( ) ( ) ( )2, 1,0 1,1, 1 1, 2,1PQ Q P= − = − − − = −��

π ( )1,1, 1P = − ( )1,2, 1rv = −�

( )1, 2,1PQ= −��

( ) ( ) ( ) ( ) ( ) ( )1 1 1

: 1 2 2 0 2 1 1 2 1 2 1 2 1 1 0

1 1 1

x

y x y z z x y

z

π−− − = → − − − − + − + − − − − = →+ −



b) Trobeu el punt M calculant el punt d’intersecció del pla amb la recta s.

Per tant el sistema format per i és: que expressat matricialment:

Per tant:

( ) ( ) ( )22 1 4 1 0 2 2 4 4 0 2 4 2 0y z y z y z ÷ −→ − − − + = → − + − − = → − − − = →

2 1 0y z→ + + =

π2 2 7 2 91 7 5

:3 21 2 10 3 2 111 2 3

x y x yx y zs

y z y z

− = + − = − + += = → → + = + − = − : 2 1 0 2 1y z y zπ + + = → + = −

s π2 9

3 2 11

2 1

x y

y z

y z

− = − = − + = −

2 3 3 3 232 1 0 9 2 1 0 9 2 1 0 9

0 3 2 11 0 1 2 1 0 1 2 1

0 1 2 1 0 3 2 11 0 0 8 8

F F F F F↔ → −− − −

− − ≅ − ≅ − − − − − −

8 8 1z z− = − → =2 1 2 1 1 2 1 3y z y y y+ = − → + ⋅ = − → + = − → = −

( )2 9 2 3 9 2 3 9 2 6 3x y x x x x− = → − − = → + = → = → =

( )3, 3,1M = −



c) Trobeu l’equació de la recta que passa pels punts P i M.

i

proporcional a i per tant l’equació continua d’aquesta recta serà:

d) Comproveu que la recta trobada en l’apartat anterior és la que busquem. Per construcció, la recta trobada passa pel punt P = (1,1,−1) i talla a la recta s en el punt M = (3,−3,1) . Per tant, solament resta per comprovar que també talla a la recta r. Un dels mètodes per a realitzar aquesta comprovació és veure que el sistema format per les equacions d’ambdues rectes i és compatible determinat,

Sumant la primera i la tercera equació tenim 4x = 8 , és a dir, x = 2 . D’aquí, a més a més, y = −1. De la segona equació, z = 0 , valor que també compleix la quarta equació. Per tant, la recta de l’apartat c) talla a la recta r en el punt (2,−1,0) . Aquest apartat es pot raonar també sense buscar el punt d’intersecció amb r. En efecte, la recta trobada a l’apartat c) passa per P i per M per construcció. Com que, a més a més. està continguda al pla , que també conté la recta r, la intersecció entre les dues està assegurada, a menys que fossin paral·leles, que no és, evidentment, el cas. NOTA: En el vostre llibre teniu un problema similar en l’exemple c) de la pàgina 132 i en l’exercici 37 d’aquesta mateixa pàgina. 50) PAU LOGSE 2008 Sèrie 4 Qüestió 4:

Donats el punt , el pla i la recta :

a) Trobeu la distància del punt P al pla .

Donat un punt i un pla sabem que

, en el nostre cas:

i

b) Trobeu la distància del punt P a la recta r.

( )1,1, 1P = − ( )3, 3,1M = − ( ) ( ) ( )3, 3,1 1,1, 1 2, 4,2PM M P→ = − = − − − = −��

( )1, 2,1v = −�

1 1 1:

1 2 1

x y zt

− − += =−

t

r t2 4 1 2 52 1

:1 2 2 11 2 1

x y x yx y zr

y z y z

− = + − = − += = → → − − = + = −−

2 2 1 2 31 1 1:

1 1 21 2 1

x y x yx y zt

x z x z

− + = − + = − − += = → → − = + − =−

π

( )7,5,1P = : 2 3 10x y zπ − − =3 2 2 7

:6 2 5

x y zr

x y z

− + = − − =

π

( )1 2 3, ,P p p p= : 0Ax By Cz Dπ + + + =

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +: 2 3 10 : 2 3 10 0x y z x y zπ π− − = → − − − =

( )( ) ( )2 22

7 2 5 3 1 10 7 10 3 10 16 16 16 14 8 14,

14 71 4 9 14 141 2 3d P π

− ⋅ − ⋅ − − − − −= = = = = =

+ ++ − + −



Recordem que la forma més ràpida de trobar la distància entre un punt P i una recta r és: Si

és un punt de la recta i és el seu vector director aleshores:

Però resulta evident que necessitem un punt i el vector director de . Per fer-ho tenim diferents mètodes. Mètode 1: Expressar la recta mitjançant la seva equació vectorial resolent el sistema que formen les seves dues equacions generals.

Així

Mètode 2: Quan tenim una recta expressada amb les seves equacions generals (és a dir, com a intersecció de dos plans) el vector director de la recta és el producte vectorial dels vectors normals d’aquestos plans. En el nostre cas:

proporcional a

. Ara solament necessitem aconseguir un punt de la recta . Mirant el sistema

amb les dues equacions podem intuir que una forma ràpida d’aconseguir un punt serà agafar . Aleshores, al sumar les dues equacions tindrem: Finalment,

substituint en la segona equació: per tant, un punt de la

recta és:

Ara ja estem en condicions d’utilitzar la fórmula de la distància:

i

c) Trobeu la distància de la recta r al pla .

Q

rv� ( ),

r

r

PQ vd P r

v

×=

��

�

r

3 2 2 7 3 2 7 2 3 2 7 2:

6 2 5 6 5 2 6 5 2zx y z x y z x y

rx y z x y z x y

λ λλ

=− + = − = − − = − → → − − = − = + − = +

7 2 2

5 2 6 42 12 10 4 16 322

3 2 18 2 16

1 6

x

λλ λ λ λ λ

− −+ − − + + + −= = = = − +

− − + −−

12 2

3 7 2

1 5 2 15 6 7 2 8 83 2 18 2 16

1 6

y λ

λλ λ λ λ −

−+ + − + += = = = −− − + −−

( ) ( ) ( ) ( ) ( )1 1 12 2 2 2, , 2, , , , 2, ,0 1, ,1x y z x y zλλ λ λ− − −= − + − → = + − →

( ) ( ) ( )12, , 2, ,0 2,1, 2x y z λ−→ = + −

( ) ( ) ( )3 2 2 7: 3, 2,2 1, 6, 2 16,8, 16

6 2 5 r

x y zr v

x y z

− + =→ = − × − − = − − − =

�

( )2,1, 2rv = −�r

0y = 4 12 3x x= → =

6 2 5 2 6 5 3 6 0 5 2 2 1x y z z x y z z− − = → = − − = − ⋅ − → = − → = −

( )3,0, 1Q = −

( ) ( ) ( )1 112 22, ,0 7,5,1 5, , 1PQ Q P − −= − = − = − −

��( )2,1, 2rv = −�

( ) ( ) ( )( )

( )( )

( )( )

22 2112

22 2

5, , 1 2,1, 2 12, 12,6 12 12 6,

2,1, 2 2,1, 2 2 1 2

r

r

PQ vd P r

v

−× − − × − − + − += = = = =

− − + + −

��

�

144 144 36 324 186

34 1 4 9

+ += = = =+ +

π



Recordem que abans de calcular distàncies entre elements de l’espai hem de mirar la seva posició relativa. En aquest cas, solament podrem calcular la distància entre la recta i el pla si aquests són paral·lels. Però per a que una recta sigui paral·lela a un pla s’ha de

complir que el vector director de la recta i el vector normal al pla

siguin perpendiculars. Comprovem si és aquest el cas:

no perpendiculars es

tallen en un punt


Les rectes i són coplanàries (és a dir, estan

incloses en un mateix pla). a) Expliqueu, raonadament, quina és la posició relativa d’aquestes rectes. Si dues rectes són coplanàries no es poden creuar. Per tant, han de tallar-se o ser paral·leles.

Però els seus vectors directors són i que evidentment no són

proporcionals. Per tant, les dues rectes no són paral·leles i per tant es tallen. b) Trobeu la relació que hi ha entre els paràmetres a i b.

i

Per tant, el sistema format per les quatre equacions escrit en forma matricial és:

Si les rectes i es tallen aleshores s’ha de complir que ,

, per tant, les files 3 i 4 de la matriu anterior han de ser proporcionals

(Pensa que si no fossin proporcionals aleshores tindríem que )

Així i proporcionals, i per tant:

c) Trobeu els valors de a i b si el pla que les conté passa pel punt P = (2, 4, 6).

Sigui el pla que conté les dues rectes i . Aleshores, donat que tota la recta està

continguda en , el punt serà un punt de i els vectors directors de les

r πrv�

nπ�

( ) ( )2,1, 2 1, 2, 3 2 2 6 6 0r rv n v i nπ π⋅ = − ⋅ − − = − + = ≠ →� � � �r i π→

( ), 0d r π→ =

1

1:

2 1 4

x a y zr

− += = 2

2 4:

1 2 1

x y b zr

+ − −= =−

( )1 2,1,4v =� ( )2 1,2, 1v = −�

1

2 21:

4 1 4 12 1 4

x a y x y ax a y zr

y z y z

− = − = − += = → → = + − =

2

2 4 2 42 4:

2 4 21 2 1

x y b x y bx y b zr

x z x z

+ = − − = − − + − −= = → → − − = − + =−

3 3 1 4 4 2

4 4 1

2

1 2 0 1 2 0 1 2 0

0 4 1 1 0 4 1 1 0 4 1 1

2 1 0 4 0 3 0 4 2 0 3 0 4 2

1 0 1 2 0 2 1 2 0 6 0 3

F F F F F F

F F F

a a a

b b a b a

a a

→ − → +

→ −

− − − − − − ≅ ≅ − − − − − − − − − − −

1r 2r ( ) ( )'rang M rang M= =º 3n incògnites= =

( )' 4rang M =

( )0 3 0 4 2b a− − − ( )0 6 0 3 a−

( ) ( ) ( )3 4 23 3 6 4 2 3 2 4 2

6 3

b aa b a a b a

a

− − −= → − = − − − → − = − − − →−

3 8 2 4 4 2 8 3 3 2 11a b a a a b a b→ − = − − − → − + = − − → + = −

π 1r 2r 1r

π ( ) 1,0, 1Q a r= − ∈ π



rectes i que són respectivament i seran vectors directors de

. Amb aquestes dades podem calcular l’equació del pla . Aquesta serà:

Però

I de la condició de l’apartat anterior:


Donats el pla i la recta , busqueu el punt de tall,

si existeix.

Per tant, el sistema format per la recta i el pla és:

Per tant, el punt de tall entre la recta i el pla és:

NOTA: Per comprovar si la solució que hem trobat és correcta, donat que aquest punt a de pertànyer a la vegada a la recta i al pla podem substituir en les seves equacions. Evidentment el punt ha de complir tant les equacions de com l’equació de . 53) PAU LOGSE 2009 Sèrie 1 Qüestió 2:

Considereu en l’espai les rectes r i s, les equacions respectives de les quals són:

i en què m és un paràmetre real.

Estudieu si hi ha cap valor d’aquest paràmetre per al qual les rectes siguin perpendiculars i es tallin.

Les rectes i seran perpendiculars sii o són els seus vectors directors i sii

1r 2r ( )1 2,1,4v =� ( )2 1,2, 1v = −�

π π2 1

: 1 2 0 3 2 3 1 0

1 4 1

x a

y x y z a

z

π−

= → − − − − =+ −

( )2,4,6 3 2 2 4 6 3 1 0 3 9 0 3 9 3P a a a aπ= ∈ → ⋅ − ⋅ − − − = → − − = → = − → = −

( )3 2 11 3 3 2 11 9 2 11 2 2 1a b b b b b+ = − → ⋅ − + = − → − + = − → = − → = −

: 3 2 5 6x y zπ − + =1 1 2

:2 1 3

x y zr

− + += =−

( ) ( )( )

1 1 2 1 1 2 2 2 31 1 2:

3 3 2 3 52 1 3 3 1 2

x y x y x yx y zr

y z y zy z

− = + − = + − = − + + = = → ≅ ≅ − − = + − − =− − + = + r π

3 3 1 2 2

3 3

3 4

3

2 3 1 2 0 3 1 2 0 3

3 5 0 3 1 5 0 3 1 5

3 2 5 6 3 2 5 6 0 4 5 3

F F F F F

F F

x y

y z

x y z

→ − →

→

− = − − − − = → − − ≅ − − ≅ − + = − −

3 3 22 2

3 3

4

3

1 2 0 3 1 2 0 3

0 12 4 20 0 12 4 20

0 12 15 9 0 0 11 11

F F FF F

F F

→ +→

→

− − ≅ − − ≅ − − −

11 11 1z z= → =112 4 20 12 4 20 12 24 2zy z y y y=− − = → − − = → − = → = −

22 3 4 3 1yx y x x=−− = → + = → = −

( ) ( ), , 1, 2,1P x y z= = − −

r πP r π

3ℝ

( ) ( ) ( ): , , 4,1,0 ,1,1r x y z mλ= +2 0

:1

x y mzs

x y z

+ + = + + =

r s rv�

sv�

0r sv v⋅ =� �

( ) ( ) ( ) ( ): , , 4,1,0 ,1,1 ,1,1rr x y z m v mλ= + → =�



Ara podem resoldre el sistema per Cramer o també restant les dues equacions. Restant-les

tenim:

Així

Finalment

Per tant sabem que hi ha dos valors per als quals les dues rectes són perpendiculars. Ara ens queda per saber si en algun d’aquestos valors es compleix també que les dues rectes es tallen. Sabem que dues rectes tenen 4 posicions relatives (Coincidents, Paral·leles, es tallen , i es

creuen) però en els casos que estem estudiant aquestes rectes són

perpendiculars, per tant no poden ser ni coincidents ni paral·leles. Així ens queda per determinar, per a cada valor, i si i es tallen o es creuen. CAS :

Sigui i proporcional a

i es tallen

Però i es creuen.

CAS :

Sigui i proporcional a

i es tallen

2 0 2 2:

1 1 1zx y mz x y mz x y m

sx y z x y z x y

λ λλ

=+ + = + = − + = − → → + + = + = − + = −

( )1 1 1y m y mλ λ λ= − − + → = − + −

( ) ( )1 1 1 1 1 1 2 2x y x m x m x mλ λ λ λ λ λ λ+ = − → − + − = − → = − + − + → = + −

( ) ( ) ( )( ) ( ) ( ) ( ): , , 2 2 , 1 1 , , , 2, 1,0 2,1 ,1s x y z m m x y z m mλ λ λ λ= + − − + − → = − + − − →

( )2,1 ,1sv m m→ = − −�

( ) ( ) ( )0 ,1,1 2,1 ,1 0 2 1 1 0r sv v m m m m m m⋅ = → ⋅ − − = → − + − + = →� �

2 2 12 1 1 0 3 2 0

2

mm m m m m

m

=→ − + − + = → − + = → =

( )1 2m i m= =

1m= 2m= r s

1m=( ) ( )1,1,1 1,1,1m

r rv m v== → =� �

( ) ( )12,1 ,1 1,0,1ms sv m m v== − − → = −� �

( )4,1,0P r= ∈ ( ) ( )2, 1,0 2, 2,0Q s PQ= − ∈ → = − −��

( )' 1,1,0PQ =��

r s

1 1 1

, , 0 , , ' 0 1 0 1 0

1 1 0r s r sv v PQ v v PQ

− ↔ = ↔ = ↔ =

��

1 1 1

1 0 1 1 0

1 1 0

r

−= − ≠ → s

2m=( ) ( )2,1,1 2,1,1m

r rv m v== → =� �

( ) ( )22,1 ,1 0, 1,1ms sv m m v== − − → = −� �

( )4,1,0P r= ∈ ( ) ( )2, 1,0 2, 2,0Q s PQ= − ∈ → = − −��

( )' 1,1,0PQ =��

r s

2 0 1

, , 0 , , ' 0 1 1 1 0

1 1 0r s r sv v PQ v v PQ ↔ = ↔ = ↔ − =

��



En aquest cas i es tallen.

Per tant la resposta al problema era .

NOTA: També haguéssim pogut començar el problema a l’inrevés, imposant primer que les

rectes i es tallen i desprès comprovar que pel valor obtingut les rectes són a

més perpendiculars.

En aquest el raonament seria, , i donat i

sabem que proporcional a

Aleshores i es tallen

Una vegada sabem que l’únic valor per al qual i es tallen és solament resta per comprovar que a més ho fan perpendicularment. Per mirar-ho cal comprovar simplement si

.

Però:

,

i


Donats el pla i el punt

a) Calculeu l’equació contínua de la recta r que passa per P i és perpendicular a .

i

l’equació contínua serà:

b) Calculeu el punt simètric del punt P respecte del pla .

Per trobar el simètric del punt respecte del pla fem el següent: 1) Trobem el punt d’intersecció entre la recta r i el pla .

2) Finalment

1) Trobem el punt d’intersecció entre la recta r i el pla .

Per tant, el sistema format per i serà:

2 0 1

1 1 1 0

1 1 0

r− = → s

2m=

r s ( )2m=

( ),1,1rv m=� ( )2,1 ,1sv m m= − −�P r∈ Q s∈

PQ��

( )1,1,0

r s

2 1

, , 0 1 1 1 0 2 0 2

1 1 0r s

m m

v v PQ m m m

− ↔ = ↔ − = → − = → =

��

r s 2m=

0r sv v⋅ =� �

( ) ( )2,1,1 2,1,1mr rv m v== → =� � ( ) ( )22,1 ,1 0, 1,1m

s sv m m v== − − → = −� �

( ) ( )2,1,1 0, 1,1 0r s r sv v v v r s⋅ = ⋅ − = → ⊥ → ⊥� � � �

: 2 0x y zπ + − = ( )3,2,1P =π

( ) ( ) ( ) ( )1,2, 1 : , , 3,2,1 1,2, 1rr v n r x y z kππ⊥ → = = − → = + −� �

3 2 1:

1 2 1

x y zr

− − −= =−

πP π

Q π

'P Q PQ= +��

Q π

( )( )

2 3 2 2 6 2 2 43 2 1:

3 1 41 2 1 3 1

x y x y x yx y zr

x z x zx z

− = − − = − − = − − − = = → ≅ ≅ − + = − + =− − − = − π r



3 3 22 2 1

3 3 1

22 0 1 2 1 0 1 2 1 0 1 2 1 0

2 4 2 1 0 4 0 5 2 4 0 5 2 4

4 1 0 1 4 0 2 2 4 0 3 0 0

F F FF F F

F F F

x y z

x y

x z

→ −→ −

→ −

+ − = − − − − = → − ≅ − ≅ − + = −

3 0 0y y= → =05 2 4 2 4 2yy z z z=− + = → = → =

( )02

2 0 2 0 2 2,0,2yz

x y z x x Q==+ − = → − = → = → =

( ) ( ) ( )2,0,2 3,2,1 1, 2,1PQ Q P= − = − = − −��

( ) ( ) ( )' 2,0, 2 1, 2,1 1, 2,3P Q PQ= + = + − − = −��




Siguin P = (3 – 2a, b, –4), Q = (a – 1, 2 + b, 0) i R = (3, –2, –2) tres punts de l’espai . a) Calculeu el valor dels paràmetres a i b per als quals aquests tres punts estiguin alineats.

, i alineats i proporcionals.

i proporcionals

b) Trobeu l’equació contínua de la recta que els conté quan estan alineats.

Sabem que els punts , i estan alineats quan i .

Substituint per aquestos valors tenim que , i el vector és

proporcional a .

Així, la recta que conté a aquestos punts és la recta que passa pel punt

amb vector director amb equació continua:

c) Quan b = 0, trobeu els valors del paràmetre a perquè la distància entre els punts P i Q sigui la mateixa que la distància entre els punts P i R.

, i

Si aleshores els punts queden: , i

i per tant:

d) Si b = 0, calculeu el valor del paràmetre a perquè els punts P, Q i R determinin un triangle equilàter. Si els punts , i determinen un triangle equilàter, aleshores per definició de triangle equilàter, els seus tres costats mesuraran el mateix. És

3ℝ

P Q R PQ↔��

PR��

( ) ( ) ( )1, 2 , 0 3 2 , , 4 3 4, 2, 4PQ Q P a b a b a= − = − + − − − = −��

( ) ( ) ( )3, 2, 2 3 2 , , 4 2 , 2 , 2PR R P a b a b= − = − − − − − = − −��

PQ��

PR�� 3 4 3 44

2 2 2

2 4 22 2 2

23 4 2 4

2 2 2 2

a aa a

b b

a

a b

− −

− − − −

= = −↔ = = → → → − − = =

3 4 4 4 3 4 4

2 4 2 2 4 2 3

a a a a a

b b b

− = − = − = − ↔ → → = − − = − − = −

P Q R 4a = − 3b = −( )11, 3, 4P = − − ( )5, 1,0Q = − − PQ

��

( ) ( )43 4, 2, 4 16,2,4aPQ a PQ=−= − → = −��

( )8,1,2v = −�

r ( )11, 3, 4P = − −

( )8,1,2v = −�

( ) ( )3 411 11 3 4: :

8 1 2 8 1 2

y zx x y zr r

− − − −− − + += = → = =− −

( )3 2 , , 4P a b= − − ( )1, 2 , 0Q a b= − + ( )3, 2, 2R= − −

0b = ( )3 2 , 0, 4P a= − − ( )1, 2, 0Q a= −

( )3, 2, 2R= − −

( ) ( ) ( )1, 2, 0 3 2 , 0, 4 3 4, 2, 4PQ Q P a a a= − = − − − − = −��

( ) ( ) ( )3, 2, 2 3 2 , 0, 4 2 , 2, 2PR R P a a= − = − − − − − = −��

( ) ( ) ( ) ( ), , 3 4, 2, 4 2 , 2, 2d P Q d P R PQ PR a a= ↔ = ↔ − = − →��

( ) ( ) ( ) ( ) ( ) ( )2 2 2 2 2 22 2 2 2 2 23 4 2 4 2 2 2 3 4 2 4 2 2 2a a a a→ − + + = + − + → − + + = + − + →

2 2 2

145

29 24 16 4 16 4 4 4 5 24 28 0

aa a a a a

a

=→ − + + + = + + → − + = → =

P Q R



a dir: Però per l’apartat c) d’aquest mateix problema sabem

que si per a que es doni la primera igualtat, és a dir, s’ha de

complir que o .

Per tant, ara es tractarà de determinar quin d’aquests dos valors fa que es doni també la 2a igualtat.

Sabem que quan aleshores: , i

I per tant:

Estudiem els dos casos: • CAS 1:

Per tant en aquest cas els tres punts formen un triangle equilàter. • CAS 2:

Per tant en aquest segon cas els tres punts determinen un triangle isòsceles i la solució a

aquest apartat és:


Donats el punt i la recta

a) Trobeu l’equació cartesiana (és a dir, de la forma Ax + By + Cz + D = 0) del pla que passa per P i és perpendicular a la recta r.

Si el pla és perpendicular a la recta , aleshores el vector normal al pla coincidirà amb

el vector director de la recta .

Però de l’equació de la recta tenim que el seu vector director

és: . Per tant, i l’equació general

del pla serà de la forma:

Falta per determinar el paràmetre . Aquest el calcularem a partir de que .

( ) ( ) ( ), , ,d P Q d P R d R Q= =

0b = ( ) ( )( ), ,d P Q d P R=2a = 14

5a =

0b = ( )3 2 , 0, 4P a= − − ( )1, 2, 0Q a= − ( )3, 2, 2R= − −

( ) ( ) ( )1, 2, 0 3 2 , 0, 4 3 4, 2, 4PQ Q P a a a= − = − − − − = −��

( ) ( ) ( )3, 2, 2 3 2 , 0, 4 2 , 2, 2PR R P a a= − = − − − − − = −��

( ) ( ) ( )1, 2, 0 3, 2, 2 4, 4, 2RQ Q R a a= − = − − − − = −��

2a =( ) ( ) 2 2 2, 2,2,4 2 2 4 24 2 6d P Q PQ= = = + + = =

��

( ) ( ) ( )22 2, 4, 2,2 4 2 2 24 2 6d P R PR= = − = + − + = =��

( ) ( ) ( )2 2 2, 2,4,2 2 4 2 24 2 6d R Q RQ= = − = − + + = =��

145a =

( ) ( )225

14 2 246, 3 4,2,4 ,2,4

5 5d P Q PQ

= = ⋅ − = =

��

( ) ( )285

14 2 246, 2 , 2,2 , 2,2

5 5d P R PR

= = ⋅ − = − =

��

( ) ( ) ( )6145 5

2 134, 4,4,2 ,4,2

5d R Q RQ −= = − = =

��

2a =

( )1,2,3P = 1 2 5:

2 3 1

x y zr

− + −= =−

π

π r nπ�

rv�

r

( )2,3, 1rv = −� ( )2,3, 1nπ = −�

π : 2 3 0x y z Dπ + − + =D

P π∈



b) Trobeu el punt de tall entre la recta r i el pla .

Per tant, el sistema format per i és:

que matricialment podem escriure com:

Així, el punt de tall entre la recta i el pla és:

57) PAU LOGSE 2009 Sèrie 4 Problema 2: Siguin r i s dues rectes de l’espai les equacions respectives de les quals, que depenen d’un

paràmetre real b, són les següents: ,

a) Trobeu el punt de tall de la recta r amb el pla d’equació x = 0 i el punt de tall de la recta s amb aquest mateix pla.

• Tall de la recta amb el pla . El sistema format per la recta i el pla és:

• Tall de la recta amb el pla .

( )1,2,3 2 1 3 2 3 0 2 6 3 0 5 0 5P D D D Dπ= ∈ → ⋅ + ⋅ − + = → + − + = → + = → = − →

: 2 3 5 0x y zπ→ + − + =

π

( ) ( )( ) ( )

3 1 2 2 3 3 2 4 3 2 71 2 5:

1 2 10 2 112 3 1 1 1 2 5

x y x y x yx y zr

x z x zx z

− = + − = + − = − + − = = → → → − + = − − − = −− − − = −

r π3 2 7

2 11

2 3 5

x y

x z

x y z

− =− − = − + − = −

12 21 2 2 2 1 2

3 3 1

3

2

3 2 0 7 1 0 2 11 1 0 2 11

1 0 2 11 3 2 0 7 0 2 6 26

2 3 1 5 2 3 1 5 0 3 5 27

F FF F F F F

F F F

→↔ → +

→ +

− − − − − − − − − − ≅ − ≅ − − − ≅ − − − − − −

12 2 3 3 22 3

1 0 2 11 1 0 2 11

0 1 3 13 0 1 3 13

0 3 5 27 0 0 14 66

F F F F F→ → +− − − − − − ≅ − − − ≅ − − − − − − −

66 66 3314 14 714 66z z −

−− = − → = = =33 99 91 99 87 7 7 73 13 13 3 13 3 13y z y z − −− − = − → = − = − ⋅ = − = =

33 66 77 66 117 7 7 72 11 11 2 11 2 11x z x z −− − = − → = − = − ⋅ = − = =

r π ( )8 33117 7 7, ,Q −=

3 1:

2 5 1

bx y zr

x y z

+ + = + + =

1:

1 1 1

x y b zs

b

− + = = + −

r 0x =r : 0xπ =

2 2 12

3 1 0 3 1 3 1 3 1

2 5 1 0 2 5 1 2 5 1 1

0 0 0 0

F F F

bx y z b y z y z y z

x y z y z y z z

x x x x

→ −

+ + = ⋅ + + = + = + = + + = → + + = → + = → − = − → = = = =

( ) ( )3 1 2 , , 0, 2,1y y x y z→ + = → = − → = −

s 0x =( ) ( )1 11

:1 1 1 1 1

b x y b b x y bx y b zs

b x z x z

+ = − + − = − − + = = → → + − − = + + = −




b) Calculeu un vector director per a cada una de les dues rectes.

• Vector director de la recta :

Recordem que quan ens donen una recta amb la seva equació general, és a dir, com a intersecció de dos plans, aleshores el vector director de la recta és el producte vectorial dels dos vectors normals d’aquestos plans. En el nostre cas:

NOTA: També podríem calcular per exemple l’equació vectorial de la recta i a partir d’aquesta trobar el vector director però utilitzant aquesta opció els càlculs resulten força llargs.

• Vector director de la recta :

En aquest cas, donat que tenim la recta expressada mitjançant la seva equació continua

tenim directament que el seu vector director és:

c) Estudieu la posició relativa de les dues rectes en funció del paràmetre b. Utilitzant els resultats de l’apartat a) tenim que el sistema format per les rectes i és:

Aleshores:

s : 0xπ =( ) ( )

( ) ( )1 1 0

1 0 1 1 , , 0, , 1

0 0 0

b x y b b y b y b

x z z z x y z b

x x x

+ − = − + ⋅ − = − − = − + = − → + = − → = − → = − = = =

3 1:

2 5 1

bx y zr

x y z

+ + = + + =

( ) ( ),1,3 1,2,5 1 3 5 2 3 6 5

1 2 5r

i j k

v b b i bk j k i bj= × = = + + − − − =

��

� ��

( ) ( ) ( )3 5 2 1 1, 3 5 , 2 1i b j b k b b= − + − + − = − − −��

1:

1 1 1

x y b zs

b

− + = = + −s

( )1, 1, 1b+ −

r s

( )1 4

3 1 1 3 1 1 0 1 1

2 5 1 1 2 5 1 1 2 5 1

1 1 1 0 1 1 0

1 0 1 1 1 3 11

F F

bx y z b

x y z

b x y b b b b b

bx z

↔

+ + = − + + = → ≅ ≅

+ − = − + − − + − − −+ = −

( )2 2 1

3 3 1

4 4 1

1

F F F

F F b F

F F bF

→ −≅ → − +

→ −

12 2 3 3 22

4 4 2

1 0 1 1 1 0 1 1

0 2 4 2 0 1 2 1

0 1 1 1 0 1 1 1

0 1 3 1 0 1 3 1

F F F F F

F F Fb b

b b b b

→ → +

→ −

− − ≅ ≅ ≅ − − − − − − − + − +

3 3 2 4 4 3

4 4 2

1 0 1 1 1 0 1 1

0 1 2 1 0 1 2 1

0 0 1 2 0 0 1 2

0 0 1 0 0 0 2

F F F F F F

F F F b b

b b b

→ + → −

→ −

− − ≅ ≅ − + − + − + −



• Si es tallen en

un punt.

• Si aleshores són paral·leles.

• Si es creuen.

NOTA: Si mireu la solució que proposen a l’examen de les PAU, per resoldre aquest apartat ells utilitzen un altre raonament que nosaltres parcialment també hem fet a classe. 58) PAU LOGSE 2010 Sèrie 1 Qüestió 1: Trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que conté la

recta i és paral·lel a la recta .

• En primer lloc escriurem la recta amb tots 3 termes expressats de la forma :

• Anomenem al pla buscat.

Si conté la recta , aleshores, el punt que pertany a també serà un punt

de , i el vector director de , serà també un vector director de .

Com és paral·lel a la recta , el vector director de serà vector director de .

Calculem, per tant, el vector de

Quan tenim una recta expressada com a intersecció de dos plans podem calcular el vector director de la recta com el producte vectorial dels vectors normals d’aquests plans.

Així:

que si el canviem de signe per estalviar signes menys tenim que .

• Finalment, construïm el pla , com el pla que passa pel punt i té vectors

directors i .

NOTA: També podríem treure el vector director de la recta calculant la seva equació

vectorial.

( ) ( )2 ' 3 º . . .b Rang M Rang M n incògnites S C D r i s= → = = = → →

1b = ( ) ( )2 3 ' . .rang M Rang M S I r i s= ≠ = → →

( ) ( )1 2 3 4 . .b b Rang M Rang M S I r i s≠ ∧ ≠ → = ≠ = → →

1

1: 2

2

xr y z

− = = − 2

0:

2 0

x y zr

x y z

− − = − + =

1r1

1

x a

v

−

ππ 1r ( )1,0,2P = 1r

π 1r ( )1 2,1, 1v = − π

π 2r 2r π

2

0:

2 0

x y zr

x y z

− − = − + =

( ) ( )2 1, 1, 1 1, 2,1 1 1 1 2 2 3 2

1 2 1

i j k

v i k j k i j i j k= − − × − = − − = − − − + − − = − − − =−

��

� � ��

( )3, 2, 1= − − − ( )2 3,2,1v =�

π ( )1,0,2P =

( )1 2,1, 1v = − ( )2 3,2,1v =�

1 2 3

: 1 2 0 : 1 3 4 8 3 6 2 2 2 0

2 1 1

x

y x y z z x y

z

π π−

= → − − + − − + + − − = →− −

3 5 5 0x y z→ − + − =

2r




Donades les rectes i :

a) Comproveu que són paral·leles. Per comprovar que dues rectes són paral·leles és suficient comprovar que els seus vectors directors són proporcionals i que si agafem un punt d’una recta, aquest punt no pertany a l’altra recta.

La recta ve definida per la intersecció de dos plans. Per trobar el vector director d’una recta

definida com intersecció de dos plans fem el producte vectorial dels vectors normals a cadascun dels plans. Així:

Per tant, els dos vectors directors són proporcionals. Fins ara sabem que els vectors directors de les dues rectes són proporcionals. Això vol dir que les rectes o bé són paral·leles o bé són coincidents. Per veure que són paral·leles agafarem un punt d’una recta i veurem que aquest punt no pertany a l’altra recta.

Sigui . Vegem que .

Substituint en les equacions de tenim:

Així no pertany a la recta perquè no compleix la segona equació i podem afirmar que les

dues rectes són paral·leles. b) Trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté. • Podem trobar un únic pla que conté dues rectes si aquestes es tallen o si són paral·leles no coincidents. • En la figura adjunta podem observar que si dues rectes i

són paral·leles, per aconseguir el pla que les conté és

2 2 1

2

0 1 1 1 0 1 1 1 0:

2 0 1 2 1 0 0 1 2 0

F F Fx y zr

x y z

→ −− − = − − − − → ≅ − + = − − 2 0 2y z y z− + = → =

0 2 0 3x y z x z z x z− − = → − − = → =

( ) ( ) ( ) ( ) ( ) ( )2 2 2: , , 3 ,2 , : , , 0,0,0 3,2,1 3,2,1r x y z z z z r x y z vλ= → = + → =�

1

5 1 2:

3 2 4

x y zr

+ − −= =− 2

2 2 5 0:

2 11 0

x y zr

x y z

+ + + = − + + =

( )1 1

5 1 2: 3,2, 4

3 2 4

x y zr v

+ − −= = → = −−

�

2r

( ) ( ) ( )2 2,1,2 2, 1,1 2 1 2 2 4 2 2 2 3 2 4 3,2, 4

2 1 1

i j k

v i k j k i j i j k= × − = = − + − + − = + − = −−

��

� � ��

( ) 15,1,2P r= − ∈ 2P r∉P 2r

( ) ( )( )

5,1,22

2 5 1 2 2 5 10 1 4 5 10 10 02 2 5 0:

2 11 0 2 5 1 2 11 10 1 2 11 11 13 2 0Px y z

rx y z

= − ⋅ − + + ⋅ + = − + + + = − + =+ + + = → − + + = ⋅ − − + + = − − + + = − + = ≠

P 2r

1r

2r



suficient aconseguir un punt i de cada recta i formar un vector .

• Com ja sabem que solament necessitarem un punt

Si fem tenim

Per tant,

• Construïm el vector

• Finalment podem construir el pla que passa pel punt i té com a vectors

directors i .


Donats el pla i la recta , estudieu-ne la posició relativa

en funció del paràmetre a. • Creem el sistema format pel pla i la recta:

Com la matriu de coeficients és quadrada és molt útil utilitzar determinants. Així:

• Per tant, hem d’estudiar els casos i : Cas :

P Q PQ��

( ) 15,1,2P r= − ∈ 2Q r∈

2

2 2 5 0:

2 11 0

x y zr

x y z

+ + + = − + + =

0z=2 5 0 2 5

4 16 42 11 0 2 11

Sumantx y x yx x

x y x y

+ + = + = − → → = − → = − − + = − = −

( )2 5 2 4 5 8 5 5 8 3x y y y y y+ = − → ⋅ − + = − → − + = − → = − + → =

( ) 24,3,0Q r= − ∈

( ) ( ) ( )4,3,0 5,1,2 1,2, 2PQ Q P= − = − − − = −��

( )5,1,2P = −

( )1 3,2, 4v = −� ( )1,2, 2PQ= −��

5 3 1

: 1 2 2 0

2 4 2

x

y

z

π+− = →− − −

( ) ( ) ( ) ( ) ( ) ( )4 5 4 1 6 2 2 2 8 5 6 1 0x y z z x y→ − + − − + − − − + + + − = →

( ) ( ) ( )4 5 2 1 4 2 0 4 20 2 2 4 8 0x y z x y z→ + + − + − = → + + − + − = →24 2 4 10 0 2 2 5 0x y z x y z÷→ + + + = → + + + =

: 5 3 4x y zπ + + =2

:2 3

ax yr

y z

− = + = −

5 3 4 5 1 3 4

2 ' 1 0 2

2 3 0 2 1 3

x y z

ax y A a

y z

+ + = − = → = −

+ = − −

5 1 3

1 0 5 6 0 0 0 5 5 0 5 5 1

0 2 1

A a a a a a a= − = − + + − − − = − = → = → =

1a = 1a ≠

1a =



La recta i el pla són paral·lels.

Cas :

En aquest cas i es tallen en

un punt. NOTA 1: Si haguéssim volgut raonar per Gauss sense utilitzar el determinant, l’argument hagués estat el següent:

Per a que les dues últimes files de la matriu siguin proporcionals s’ha de complir que

obtenint evidentment els mateixos

casos que abans. NOTA 2: També podríem resoldre el problema per un procediment més geomètric i no tant algèbric. Seria el següent: Un pla i una recta a l’espai poden ser paral·lels, tallar-se en un punt o la recta pot estar continguda en el pla.

Sigui el vector normal al pla . Evidentment

Calculem ara el vector director de la recta . Aquest serà:

La recta i el pla es tallaran si els vectors i no són

perpendiculars, és a dir, si

Per tant, en el cas en que , la recta i el pla es tallaran.

12 232 2 12 1 5

5 1 3 4 1 1 0 2 1 1 0 2

' 1 1 0 2 5 1 3 4 0 6 3 6

0 2 1 3 0 2 1 3 0 2 1 3

FF F FF F F

A↔ →→ −

− − = − ≅ ≅ − ≅ − − −

3 3 2

1 1 0 2 1 1 0 2

0 2 1 2 0 2 1 2

0 2 1 3 0 0 0 1

F F F→ −− −

≅ − ≅ − − −

( ) ( )2 3 ' . .Rang A Rang A S I= ≠ → → r π

1a ≠( ) ( )3 ' º . . .Rang A Rang A n incògnites S C D r= = = → → π

2 2 15 2 255 3 10 45 5 5

5 1 3 4 5 1 3 4 5 1 3 4

' 1 0 2 0 0 5 3 10 4

0 2 1 3 0 2 1 3 0 2 1 3

aF F F F Fa a aA a a a a

→ − →− − − −

= − ≅ ≅ − − − − − − −

A5 3

5 6 5 5 12 1

a aa a a a

− − −= → − − = − → − = − → =

vπ� π ( )5,1,3vπ =�

r

( ) ( ), 1,0 0,2,1 1 0 2 0 0 0 2

0 2 1r

i j k

v a a i ak j k i aj i aj ak= − × = − = − + + + − − = − − + =

��

� � ��

( )1, , 2a a= − −

nπ�

rv�

0rn vπ ⋅ ≠� �

( ) ( )5,1,3 1, , 2 5 6rn v a a a aπ ⋅ = ⋅ = − − = − − + =� �

5 5 0 5 5 1a a a= − + = → = → =1a ≠



En l’altre cas, és a dir, quan , tenim dues possibilitats, que la recta i el pla siguin paral·lels o que la recta estigui continguda en el pla. Per decantar-nos per un cas o l’altre agafem un punt de la recta i comprovem si aquest punt pertany al pla. Així:

Tenim que . Comprovem si

i

paral·lels. 61) PAU LOGSE 2010 Sèrie 2 Qüestió 6:

Considereu la recta .

a) Trobeu els dos punts, A i B, de la recta r que estan situats a una distància del punt P = (–1, 1, 2). • En aquest tipus de problema ens interessa ficar la recta expressada amb la seva equació vectorial perquè així depèn d’un paràmetre que és el que després forçarem a complir la propietat que ens demanen. Així:

Un punt genèric de la recta és

• En la imatge adjunta podem apreciar que en principi, donat el punt P i la recta r, hi haurà dos

punts A i B de r que estaran a una distància de P. • Calculem ara, la distància entre aquest punt

de la recta i el punt que ens dóna l’enunciat.

1a =

( ) ( )1 : 02 2 0 2: , , 2,0, 3

2 3 2 3 3a yax y x y x

r x y zy z y z z

= =− = − = − = → → → = − + = − + = − = −

( )2,0, 3P r= − ∈ P π∈( ) ( )2,0, 3:5 3 4 5 2 0 3 3 10 0 9 1 4Px y z P r rπ = −+ + = → ⋅ + + ⋅ − = + − = ≠ → ∉ → π

4 1: 1

2 1

x yr z

+ −= = −− −

6d =

( ) ( ) ( )4 1: 1 , , 4,1,1 2, 1,1

2 1

x yr z x y z λ+ −= = − → = − + − − →

− −( ) ( ), , 4 2 , 1 , 1x y z λ λ λ→ = − − − +

r ( )4 2 , 1 , 1Q λ λ λ= − − − +

6

Q

( )1,1,2P = −

( ) ( ) ( )4 2 , 1 , 1 1,1,2 3 2 , , 1PQ Q P Q λ λ λ λ λ λ= − = = − − − + − − = − − − − +��

( ) ( ) ( ) ( ) ( )2 2 2, 3 2 , , 1 3 2 1d P Q PQ λ λ λ λ λ λ= = − − − − + = − − + − + − + =

��

2 2 2 29 12 4 1 2 6 10 10λ λ λ λ λ λ λ= + + + + − + = + +

( ) 2 2, 6 6 10 10 6 6 10 10 6d P Q λ λ λ λ= →= + + = → + + = →

2

23

16 10 4 0

λλ λ

λ −

= −→ + + = → =



b) Trobeu l’àrea del triangle de vèrtexs A, B i P.

L’àrea d’un triangle és . En el nostre cas, mirant la figura anterior,

agafarem com a base del triangle la distància entre els punts A i B i com altura del triangle la distància entre el punt P i la recta r.

on és punt qualsevol de la recta r i és el vector director de r.

Agafant tenim:

Finalment:

NOTA: Aquest apartat també es pot resoldre utilitzant que el mòdul del producte vectorial dels

vectors i és l’àrea del paral·lelogram que formen, per tant, l’àrea del nostre triangle

serà la meitat, és a dir, .

62) PAU LOGSE 2010 Sèrie 4 Qüestió 1: Donats el pla i els punts P = (3, 1, –2) i Q = (0, 1, 2):

a) Calculeu l’equació contínua de la recta perpendicular al pla que passa pel punt P.

( )( )

( )8 52 13 3 3 3

1 2,2,04 2 , 1 , 1

, ,

AQ

B

λλ λ λ

λ −−

= − → = −

= − − − + → = → =

2

base alturaA

×=

( ) ( ) ( )8 5 1 2 1 13 3 3 3 3 3, , 2, 2, 0 , ,AB B A − − −= − = − − =

��

( ) ( ) ( ) ( ) ( )2 2 2 662 1 1 2 1 1 4 1 1 23 3 3 3 3 3 9 9 9 9 3 3, , ,d A B AB − − − −= = = + + = + + = = =

��

( ),QP v

d P rv

×=

��

� Q v�

( )2,2,0Q A= = −

( ) ( ) ( )1,1,2 2,2,0 1, 1,2QP P Q= − = − − − = −��

( )4 1: 1 2, 1,1

2 1

x yr z v

+ −= = − → = − −− −

�

( )1 1 2 4 2 2 5 3 1, 5, 3

2 1 1

i j k

QP v i k j k i j i j k× = − = − − − − + − = − − = − −− −

��

��

( ) ( )( )

( ) ( )( ) ( )

2 22

2 2 2

1, 5, 3 1 5 3 1 25 9 35,

2, 1,1 4 1 1 62 1 1

QP vd P r

v

× − − + − + − + += = = = =− − + +− + − +

��

�

( ) ( ) 6, ,

2 2

d A B d P rbase alturaA

××= = =35

3 6⋅ 35

2 6=

AB��

AP��

1

2TA AB AP= ×��

: 2 3 4 0x y zπ + + − =π



Sigui r la recta buscada. Si r és perpendicular al pla aleshores el vector director de r,

coincidirà amb el vector normal a que és .

Si r també ha de complir que passa pel punt tindrem:

d’on podem deduir que l’equació continua és:

b) Calculeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla perpendicular a que passa pels punts i .

Sigui el pla buscat. En la figura adjunta podem observar que per ser perpendicular a el vector normal a serà un

vector director de . Per altra banda, si P i Q són punts de tindrem que el vector

serà un vector director de .

Per tant, podem calcular com el pla que té com a vectors

directors els vector i i que passa pel punt .

i

Així:


Donats el punt P = (1, 0, –2) i la recta :

a) Trobeu l’equació contínua de la recta que passa pel punt P i talla perpendicularment la recta r. • Sigui el pla perpendicular a r que passa per P. Per construcció, qualsevol recta continguda en tallarà perpendicularment a r. Sigui Q el punt de tall entre el pla i la recta r, la recta que passa per P i Q, estarà continguda en , per tant, tallarà

π rv�

π ( )1,2,3nπ =�

( )3,1, 2P = −

( ) ( ) ( ): , , 3,1, 2 1,2,3r x y z λ= − +

3 1 2:

1 2 3

x y zr

− − += =

π P Q

'ππ π

'π

'πPQ��

'π

'πnπ�

PQ��

P

( )1,2,3nπ =� ( ) ( ) ( )0,1,2 3,1, 2 3,0,4PQ Q P= − = − − = −��

( ) ( ) ( ) ( ) ( ) ( )3 1 3

' : 1 2 0 0 8 3 9 1 0 2 6 2 0 3 4 1 0

2 3 4

x

y x y z z x y

z

π− −− = → − − − + + + + + − − − = →+

( ) ( ) ( )8 3 13 1 6 2 0 8 24 13 13 6 12 0x y z x y z→ − − − + + = → − − + + + = →

8 13 6 1 0x y z→ − + + =

5 3 3:

2 2 3

x y zr

− − += =−

ππ

ππ



perpendicularment a r i evidentment passarà per P satisfent totes les condicions del problema. • Càlcul del pla perpendicular a r que passa per P:

• Càlcul del punt de tall entre la recta r i el pla :

• Finalment calculem la recta que passa per P i per Q:

,

b) Calculeu la distància del punt P a la recta r. Si utilitzem la fórmula de la distància entre un punt i una recta tenim:

on és punt qualsevol de la recta r i és el vector director de r.

Substituint en el nostre cas:

( ) ( ) ( )1,0, 22,2 3 2,2 3 : 2 2 3 0 Prv n x y z k π

π π = − ∈= − → = − → + − + = →� �

( )2 1 2 0 3 2 0 2 0 6 0 8 0 8k k k k→ ⋅ + ⋅ − ⋅ − + = → + + + = → + = → = − →: 2 2 3 8 0x y zπ + − − =

π35

2 2 25 3 3:

2 2 3

yxx y zr

−− = →− − += = →−

( )5 2x − = ( )5 3

2 3

3 5 3 2

3 15 2 6 3 2 9 3 2 9x z

y x y x y

x z x z x z− +−

− → − = − → − =

= → − + = + → − − = − → + =

1 2 2 2 1

3 3 1

2

3

: 2 2 3 8 0 2 2 3 8 1 1 0 2

' 1 1 0 2 2 2 3 82:

3 0 2 9 3 0 2 93 2 9

F F F F F

F F F

x y z

Ax yr

x z

π↔ → −

→ −

+ − − = − − → = − ≅ − ≅− = + =

3 3 22 2

3 3

3

4

1 1 0 2 1 1 0 2 1 1 0 2

0 4 3 4 0 12 9 12 0 12 9 12

0 3 2 3 0 12 8 12 0 0 17 0

F F FF F

F F

→ −→

→

− − − ≅ − ≅ − ≅ −

17 0 0z z= → =012 9 12 12 12 1zy z y y=− = → = → =

2 1 2 3x y x x− = → − = → =

( )3,1,0Q =

( )1,0, 2P = − ( )3,1,0Q =

( ) ( ) ( )3,1,0 1,0, 2 2,1,2PQ Q P= − = − − =��

( ) ( ) ( ) 1 2' : , , 1,0, 2 2,1,2 ' :

2 1 2

x y zr x y z rλ − += − + → = =

( ),QP v

d P rv

×=

��

� Q v�

( ) ( ) ( )2,1,2 2,2, 3 2 1 2 3 4 4 2 4 6 7 10 2 7,10,2

2 2 3

i j k

i k j k i j i j k× − = = − + + − − + = − + + = −−

��

� � ��

( ) ( ) ( )( )

( )( )

2,1,2 2,2, 3 7,10,2 49 100 4,

2,2, 3 2,2, 3 4 4 9

QP vd P r

v

× × − − + += = = = =− − + +

��

�



64) PAU LOGSE 2010 Sèrie 5 Qüestió 5: Siguin r i s dues rectes d’equacions

i

a) Trobeu el valor del paràmetre a perquè aquestes rectes es tallin. Utilitzarem el mètode genèric per comprovar la posició relativa entre dues rectes:

Restant la 1a i la 3a equació tinc que i .

Substituint en la 2a equació tinc que .

Finalment, substituint en la 4a equació tinc que

Per tant, si les rectes r i s es tallen i ho fan en el punt

NOTA: Per demostrar que les rectes r i s es tallen també es pot fer que el sistema de vectors format pels vectors directors de les dues rectes i un 3r vector que construïm mitjançant un punt de la recta r i un altre punt de la recta s tingui rang 2. Seria així:

i

i

té així:

Obtenint, evidentment el mateix resultat que abans. b) En el cas en què es tallen, trobeu l’equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté.

153 1539 3

1717= = = =

( ) ( ) ( ): , , 4,3,4 2, 1,1r x y z t= − + − 2: 1

1 3

y z as x

− −+ = =−

( ) ( ) ( ) 4 2 6 2 24 3 4: , , 4,3,4 2, 1,1

3 4 72 1 1

x y x yx y zr x y z t

y z y z

− − = − = + + − −= − + − → = = → → − = − + + =−

1 2 12: 1

3 3 3 31 3

x y x yy z as x

x z a x z a

− − = − = + − −+ = = → → + = − − = − −−

2 2

7

1

3 3

x y

y z

x y

x z a

+ = + = + = − = − −

1y = 0x =6z=

3 0 6 3 6 3 3a a a⋅ − = − − → − = − − → =

3a = ( ) ( ), , 0,1,6x y z =

( )2, 1,1rv = −� ( )1, 1,3sv = −�

( )4,3,4P r= − ∈ ( )1,2,Q a s= − ∈

( ) ( ) ( )1,2, 4,3,4 3, 1, 4PQ Q P a a= − = − − − = − −��

{ }, ,r sv v PQ��

3 , , 0Rang u v PQ= ↔ ≠��

2 1 3

1 1 1 0 2 8 9 1 3 6 4 0 3 0 3

1 3 4

a a a a

a

− − − = → − + − − + + + − = → − + = → =−



Per formar un pla necessitem un punt i dos vectors directors.

Agafarem , i , aleshores:


Donada la recta :

a) Trobeu-ne un vector director. Hi ha diferents formes de buscar aquest vector director quan la recta ve donada per la intersecció de dos plans. Potser la forma més comuna de trobar aquest vector és fer el producte vectorial dels vectors normals de cada pla. Així:

NOTA: Un mètode alternatiu seria resoldre el sistema compatible indeterminat que formen les dues equacions de la recta per trobar l’equació vectorial de la recta d’on podríem obtenir el vector director. Seria així:

Així:

b) Calculeu l’equació contínua de la recta paral·lela a r que passa pel punt P=(1, 0, −1). Sigui s la recta buscada. Per ser paral·lela a r tindrà el mateix vector director que r, per tant:

Aleshores, s passa per amb vector director , aleshores:

( )4,3,4P r= − ∈ ( )2, 1,1rv = −� ( )1, 1,3sv = −�

( ) ( ) ( ) ( ) ( ) ( )4 2 1

: 3 1 1 0 3 4 3 2 4 4 4 6 3 0

4 1 3

x

y x y z z x y

z

π+− − − = → − + + − − − + − + + − − = →−

( ) ( ) ( )2 4 5 3 4 0 2 8 5 15 4 0x y z x y z→ − + − − − − = → − − − + − + = →

: 2 5 11 0x y zπ→ − − − + =

2 3 2:

1 0

x y zr

x z

− + = + + =

( ) ( ) ( )2, 1,3 1,0,1 2 1 3 0 3 0 2 1,1,1

1 0 1r

i j k

v i k j k i j i j k= − × = − = − + + + − − = − + + = −

��

� � ��

2 3 2 2 1 3 2 1 0 1 1 1 0 1 1: '

1 0 1 0 1 1 2 1 3 2 0 1 1 4

x y zr A

x z

− + = − − − → = ≅ ≅ + + = − − −

4 4 4zy z y yλ λ λ=− + = → − + = → = −2 3 2 2 4 3 2 2 2 4 2 2 2 2x y z x x xλ λ λ λ− + = → − + + = → + + = → = − − →

2 22 1x xλ λ− −→ = → = − −

( ) ( ) ( ) ( ) ( ): , , 1 , 4, 1, 4,0 1,1,1 1,1,1rr x y z vλ λ λ λ= − − − = − − + − → = −�

( )1,1,1s rv v= = −� �

( )1,0, 1P = − ( )1,1,1sv = −�

1 0 1:

1 1 1

x y zs

− − += =−




Siguin i i .

a) Comproveu que i són perpendiculars.

Dues rectes són perpendiculars sii ho són els seus vectors directors. Dos vectors són perpendiculars sii el seu producte escalar dóna zero.

b) Comproveu que es tallen mitjançant la determinació del punt de tall.

Sumant les files 3 i 4 tenim i

Substituint en la 2a equació tenim

Finalment comprovem si també es compleix la 1a equació:

Així les rectes es tallen en el punt


Donada la recta , calculeu l’equació general (és a dir, de la forma Ax + By +

Cz +D= 0) del pla perpendicular a la recta que passa pel punt P = (1, 0, –1). Primer trobarem el vector director de la recta. Quan una recta ve donada per la intersecció de dos plans, podem trobar el vector director de la recta mitjançant el producte vectorial dels vectors d’aquests plans. En el nostre cas:

1

3 1: 2

2 2

y zr x

− −− = = 2

3 1: 1

2 2

x zr y

+ += + =

1r 2r

( )1 1

3 1 3 1: 2 : 2 1,2, 2

2 2 2 2

y z y zr x r x v

− − − −− = = → − = = → = −−

�

( )2 2

3 1: 1 2,1,2

2 2

x zr y v

+ += + = → =�

( ) ( )1 2 1 2 1 21,2, 2 2,1,2 2 2 4 0v v v v r r⋅ = − ⋅ = + − = → ⊥ → ⊥� �

32

1 13 12 2

2 2 4 3 2 1 2 13 1: 2 :

42 2 3 1 4

y

y z

x x y x y x yy zr x r

y zy z y z

−

− −

− = → − = − → − = − =− − − = = → → + == → − = − → + = 3

22 21

2

1 3 2 2 2 1 2 13 1: 1 :

2 12 2 1 2 2 1 2 1

x

z

y x y x y x yx zr y r

y zy y z y z

+

+

= + → + = + → − = − − = −+ += + = → → − = −+ = → + = + → − = −

2 3

2 1 2 1

4 2 1

2 1 4

2 1 2 1

F F

x y x y

y z x y

x y y z

y z y z

↔

− = − = + = − = − ≅ − = − + = − = − − = −

3 3 1y y= → = 3z=y 2 1 1 2 1 1x x x− ⋅ = − → − = − → =

2 2 1 1 2 1 1x y− = ⋅ − = − =

( )1,1,3P =

2 3 2

1 0

x y z

x z

− + = + + =



Estem

buscant un pla perpendicular a la recta r, aleshores, el vector normal al pla serà el vector

director de la recta r, és a dir, el pla serà de la forma:

Aleshores el pla buscat és

NOTA: Una altra manera de trobar el vector director de la recta era passar de la seva equació general a per exemple l’equació vectorial. Això es fa resolvent el sistema compatible indeterminat que suposen les dues equacions de la recta. En el nostre cas:

Així:


Considereu la recta i el pla .

a) Estudieu la posició relativa de la recta r i el pla en funció del paràmetre a.

Una recta i un pla poden tenir 3 posicions relatives. Que la recta talli al pla en un punt, que sigui paral·lela al pla o que estigui continguda en el pla. En els dos últims casos (paral·lela i continguda) podem veure que aleshores el vector director de la recta i el vector normal al pla han de ser ortogonals, és a dir el seu producte escalar ha de ser zero.

Per tant, ja sabem que o bé, r és paral·lela a o bé r està continguda en . Per decidir en quin dels dos casos ens trobem, agafem un punt de r i comprovem si pertany a

.

Sigui .

Aleshores: Si la recta està continguda en el pla i si aleshores la recta és paral·lela a . NOTA: Evidentment també es pot discutir la posició relativa de la recta i el pla resolvent el sistema d’equacions lineals que formen i utilitzar el teorema de Rouché Frobenius. Seria així:

( )( ) ( ) ( )

'

2, 1,32 3 22, 1,3 1,0,1

1 0 1,0,1r

nx y zv

x z n

π

π

= −− + = → → = − × = + + = =

��

( ) ( )2 1 3 0 3 0 2 1,1,1 1,1,1

1 0 1r

i j k

i k j k i j i j k v= − = − + + + − − = − + + = − → = −

��

� � ��

( )1,0, 10 1 0 1 0 2 0 2Px y z k k k k= −− + + + = →− + − + = → − + = → =

2 0x y z− + + + =

2 3 2 2 3 2 2 3 2

1 0 1 1 1zx y z x y z x y

x z x z x xλ λ

λ λ=− + = − + = − + = ≅ → + + = + = − + = − → = − −

( ) ( )12 3 2 2 1 3 2 2 1 3 2xx y y yλλ λ λ λ λ=− −− + = → ⋅ − − − + = → ⋅ − − + − = →2 2 3 2 4y yλ λ λ→ = − − + − → = − +

( ) ( ) ( ) ( ) ( ) ( ), , 1 , 4 , , , 1, 4,0 1,1,1 1,1,1rx y z x y z vλ λ λ λ= − − − + → = − − + − → = −�

1 2:

3 1

x yr z a

− += = −−

: 2 5 5x y zπ + − =

π

( ) ( )3, 1,1 2,1, 5 6 1 5 0rv nπ⋅ = − ⋅ − = − − =� �

π π

π( )1, 2,P a r= − ∈

( )1, 2,: 2 5 5 2 2 5 5 5 5 1P ax y z a a aπ = −+ − = → − − = → − = → = −

1a = − r π 1a ≠ − rπ



Aleshores el sistema serà:

Aleshores:

Si , .

Si , i paral·lels.

b) Quan , calculeu la distància de la recta r al pla .

En el cas en que sabem que i són paral·lels. Aleshores podrem calcular la distància entre la recta i el pla com la distància de qualsevol punt al pla .

Quan tenim que el punt

Donat un punt i un pla tenim que:

Aleshores

69) PAU LOGSE 2011 Sèrie 4 Qüestió 2: Donat el pla :

a) Calculeu l’equació del pla paral·lel al pla que passa pel punt P=(1, 0, −1).

Sigui el pla buscat: Per ser paral·lel a l’equació de és de la forma

Com aleshores:

213 1

21

1 3 6 3 5 3 51 2: :

23 1 2 2

yx

y

x y x y x yx yr z a r

y z az a y z a y z a

+−−

+−

= → − + = + → − − = − − =− + = = − → → + = −− = − → + = − + → + = −

13 33 3 1 52

3 5 1 3 0 5 1 3 0 5

2 ' 0 1 1 2 0 1 1 2

2 5 5 2 1 5 5 0 5 5 15

F FF F Fx y

y z a A a a

x y z

→→ +− − = − − − − + = − → = − ≅ − ≅

+ − = − − −

3 3 2

1 3 0 5 1 3 0 5

0 1 1 2 0 1 1 2

0 1 1 3 0 0 0 1

F F F

a a

a

→ +− − − − ≅ − ≅ − − − +

1a = − ( ) ( )' 2 3 º . .Rang A Rang A n incògnites S C I rπ= = < = → → ⊂

1a ≠ − ( ) ( )2 3 ' .Rang A Rang A S I r= ≠ = → → π

3a = π

3a = r πr π P r∈ π

3a = ( )1, 2,3P r= − ∈

( )1 2 3, ,P p p p= : 0Ax By Cz Dπ + + + =

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +

( ) ( ) ( )( )( )22 2

2 1 2 5 3 5, , 1, 2,3 , 2 5 5 0

2 1 5d r d P d x y zπ π

⋅ − − ⋅ −= = − + − − = = =

+ + −

2 2 15 5 20 20 20 30 2 30

30 34 1 25 30 30

− − − −= = = = =

+ +

: 2 5x y zπ + − =π

'ππ 'π ' : 2 0x y z kπ + − + =

( )1,0, 1 'P π= − ∈

( )' : 2 1 0 1 0 2 0 1 0 3 0 3k k k kπ ⋅ + − − + = → + + + = → + = → = − →



b) Determineu també la distància entre el punt P i el pla .

Donat un punt i un pla tenim que:

En el nostre cas i

NOTA: Donat que el punt pertany al pla també podem calcular la distància entre el punt i el pla com la distància

entre els plans paral·lels i . És a dir:

70) PAU LOGSE 2011 Sèrie 4 Qüestió 5: Calculeu l’equació general (és a dir, de la forma Ax+By+Cz+D=0) dels plans que

contenen la recta i que formen un angle de 45° amb el pla .

MÈTODE 1: Imaginant els plans solució:

' : 2 3 0x y zπ→ + − − =

π

( )1 2 3, ,P p p p= : 0Ax By Cz Dπ + + + =

( ) 1 2 3

2 2 2,

Ap Bp Cp Dd P

A B Cπ

+ + +=

+ +

( )1,0, 1P = − : 2 5 0x y zπ + − − =

( ) ( )( )22 2

2 1 0 1 5 2 0 1 5 2 2 2 6 6,

6 34 1 1 6 62 1 1d P π

⋅ + − − − + + − −= = = = = =

+ ++ + −

P 'πP π

π 'π( ) ( ), ' , 'd P dπ π π= =

( ): 2 5 0, ' :2 3 0d x y z x y zπ π= + − − = + − − = =

( )( )22 2

5 3 5 3 2 2 6

34 1 1 6 62 1 1

− − − − + −= = = = =

+ ++ + −

2:

1

yr

z

= =

0z=



En el gràfic podem observar amb color blau la recta . Per dibuixar-la solament cal

representar dos punts que compleixin les dues equacions, per exemple, els punts

i i després unir-los.

També he intentat representar, amb poc èxit, els dos plans i que contenen a la recta r i que formen un angle de 45º amb el pla horitzontal representat en color groc. • Podem observar que el pla , a banda de contenir a la recta r, passa per exemple pel punt

mentre que el pla conté a la recta r i passa pel punt , per tant, ja

tenim suficient informació per trobar les seves equacions. Restant els dos punts A i B de r obtindrem el seu vector director:

i , aleshores

• Aleshores podem construir el pla com el pla que passa pel punt i té com a

vectors directors i , així:

• Anàlogament i , restant-los obtindrem un vector director de :

Finalment podem construir el pla com el pla que passa pel punt i té com a

vectors directors i , així:

MÈTODE 2:

La recta conté tots els punts en que la coordenada val i la coordenada val

1. Per tant, passa pels punts i .

Restant-los obtenim que el vector director de és:

.

Si el pla que busquem conté la recta , aleshores el vector normal a i el vector director de seran ortogonals. És a dir, si tindrem que

.

2:

1

yr

z

= =

( )0,2,1A=

( )1,2,1B =π 'π

0z=

π( )0,3,0C = 'π ( )0,1,0D =

( ) ( ) ( ) ( )1,2,1 0,2,1 1,0,0 1,0,0rAB B A v= − = − = → =��

C π∈ A π∈ ( ) ( ) ( )0,2,1 0,3,0 0, 1,1CA A C= − = − = −��

π ( )0,2,1A=

( )1,0,0rv =� ( )0, 1,1CA= −��

( ) ( )1 0

: 2 0 1 0 1 1 1 2 0 1 2 0 : 3 0

1 0 1

x

y z y z y y z

z

π π− − = → − − − − = → − + − + = → + − =−

( )0,1,0 'D π= ∈ 'A π∈ 'π

( ) ( ) ( )0,2,1 0,1,0 0,1,1DA A D= − = − =��

'π ( )0,2,1A=

( )1,0,0rv =� ( )0,1,1DA=��

( ) ( )1 0

' : 2 0 1 0 1 1 1 2 0 1 2 0 : 1 0

1 0 1

x

y z y z y y z

z

π π− = → − − − = → − − + = → − + + =−

2:

1

yr

z

= =

y 2 z

( )0,2,1A= ( )' 1,2,1A =r

( ) ( ) ( )' ' 1,2,1 0,2,1 1,0,0rv AA A A= = − = − =��

π r πr : 0Ax By Cz Dπ + + + =

( ) ( )1,0,0 , , 0 0rv n A B C Aπ⊥ → ⋅ = → =� �



Així, donat que , el pla serà de la forma i per tant el seu vector

normal serà de la forma .

Finalment utilitzarem el fet de que el pla que estem buscant forma un angle de 45º amb el

pla que té com a vector normal

Per definició de producte escalar:

Per tant, tenim dues solucions i . Així si, per exemple fem tenim:

I en el cas en que tenim:

MÈTODE 3: Per feixos de plans:

Donada la recta sabem que el feix de plans que la conté és

i per tant,

el seu vector normal serà .

Si el pla i el pla han de formar un angle de 45º, aleshores els seus vectors

normals i també formaran el mateix angle.

Per definició de producte escalar:

0A= π : 0By Cz Dπ + + =

( )0, ,n B Cπ =�

π: 0z zπ = ( )0,0,1zn =�

�( ) ( ) ( )( ) ( ) 2 2

0, , 0,0,1 2cos , cos45º

20, , 0,0,1 1

zz

z

B Cn n Cn n

n n B C B C

ππ

π

⋅⋅= → = → = →

⋅ ⋅ + ⋅

� ��

� �

2

2 22 2

2 2 2 22 2 2 2

2 2 2 1

2 2 4 2xC C C C

B C B CB C B C

→ = → = → = → = → + ++ +

2 2 2 2 2 22B C C B C C B C B→ + = → = → = ± → = ±

C B= C B= −1B =

( )0,2,11: 0 0 0B C BBy Cz D y Cz D y z D ππ ∈= =+ + = → + + = → + + = →

2 1 0 3 : 3 0D D y zπ→ + + = → = − → + − =

C B= −( )0,2,1 '1' : 0 0 0B C BBy Cz D y Cz D y z D ππ ∈= =−+ + = → + + = → − + = →

2 1 0 1 ' : 1 0D D y zπ→ − + = → = − → − − =

2 2 0:

1 1 0

y yr

z z

= − = ≅ = − =

( ) ( ): 2 1 0 : 2 0 : 2 0y z y z y zλ λ λπ λ π λ λ π λ λ− + − = → − + − = → + − − =

( )0,1,nλ λ=�

λπ : 0z zπ =

( )0,1,nλ λ=� ( )0,0,1zn =�

( ) ( ) 2 2 2 22 2cos45º 0,1, 0,0,1 1 1 1

2 2z zn n n nλ λ λ λ λ λ⋅ = → ⋅ = + ⋅ ⋅ → = + ⋅ →� � � �

( )2 22 2 2 2 2 22 1 2 4 1 2 2 1 1xλ λ λ λ λ λ λ÷→ = + ⋅ → = + ⋅ → = + → = →

1 1λ λ→ = → = ±



71) PAU LOGSE 2012 Sèrie 1 Qüestió 1: Donats els plans i ,

a) Comproveu que són perpendiculars. Dos plans seran perpendiculars sii ho són els seus vectors normals. Així .

Dos vectors són perpendiculars sii el seu producte escalar és zero. Així:

b) Calculeu l’equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla perpendicular a

i , que passa pel punt P=(1, 3, 2).

Sigui el pla buscat. Per ser perpendicular als plans i tenim que el vector normal al

nostre pla també serà perpendicular als vectors normals a i . És a dir, per buscar el

vector normal a solament necessitem buscar un vector ortogonal a i a .

Això ho podem fer mitjançant el producte vectorial d’aquests dos vectors. És a dir:

Dividint les components del vector entre dos podem agafar el vector

Per tant, l’equació del pla és de la forma

Imposant que passi pel punt P=(1, 3, 2) tenim:


Siguin i . Estudieu-ne la posició relativa segons

el valor del paràmetre m.

1 3 0: 2 0

1 1 0

Si y zy z

Si y zλ

λπ λ λ

λ

= → + − =+ − − = → = − → − − =

1 : 3 2 15 0x y zπ + − + = 2 : 2 103 0x y zπ + + − =

1 21 2 n nπ ππ π⊥ ↔ ⊥� �

( )11 : 3 2 15 0 3,1, 2x y z nππ + − + = → = −�

( )22 : 2 103 0 1,1,2x y z nππ + + − = → =�

( ) ( )1 2 1 23,1, 2 1,1,2 3 1 4 0n nπ π π π⋅ = − ⋅ = + − = → ⊥� �

1π 2π

3π 1π 2π

3π 1π 2π

3π1

nπ�

2nπ�

( )3 1 2

3 1 2 2 3 2 2 6 4 8 2 4, 8,2

1 1 2

i j k

n n n i k j k i j i j kπ π π= × = − = + − − + − = − + = −

��

� � ��

( )3

2, 4, 1nπ = −�

3π 3 : 2 4 0x y z kπ − + + =

( ) 31,3,23 : 2 4 0 2 1 4 3 2 0 2 12 2 0Px y z k k kππ = ∈− + + = → ⋅ − ⋅ + + = → − + + = →

38 0 8 : 2 4 8 0k k x y zπ→ − + = → = → − + + =

: 3 2 1x y zπ − + =3 1

:2 1

x yr

x y mz

+ = − + =



Una recta i un pla de admeten 3 posicions relatives diferents. La recta talla al pla en un punt, la recta és paral·lela al pla o la recta està continguda en el pla. D’entrada podem resoldre l’exercici de tres formes diferents. • MÈTODE 1: Amb el teorema de Rouché-Frobenius actuant per determinants: Donat que la matriu de coeficients és una matriu quadrada podem aprofitar per calcular el seu determinant i estudiar els valors que l’anul·lin. És a dir:

. Per tant, hem d’estudiar els casos i

. Cas , en aquest cas:

Aleshores:

• Si , solucions La

recta està continguda en el pla.

• Si

La recta i el pla es tallen en un punt. • MÈTODE 2: Amb el teorema de Rouché-Frobenius esgraonant la matriu pel mètode de Gauss:

• Si solucions La

recta està continguda en el pla.

• Si La

recta i el pla es tallen en un punt. • MÈTODE 3: Podríem anomenar-lo mètode geomètric.

3ℝ

A

1 3 2

3 1 0 6 0 4 0 9 10 10

2 1

A m m m

m

− = = − + − + + = − −

0 10 10 0 10 10 1A m m m= → − = → = → = 1m=1m≠

1m=1

2 2 3 3 22 2 1 2

3 3 1

3

2

1 3 2 1 1 3 2 1 1 3 2 1

' 3 1 0 1 0 10 6 2 0 5 3 1

2 1 1 1 0 5 3 1 0 5 3 1

F F F F FF F F

F F FA

→ → −→ −

→ −

− − − = ≅ − − ≅ − − ≅ − − − − −

1 3 2 1

0 5 3 1

0 0 0 0

− ≅ − −

1m= ( ) ( )' 2 3 º . .Rang A Rang A n incògnites SC I= = < = → → ∞ →

1m≠ ( ) ( )0 ' 3 º . .A Rang A Rang A n incògnites SC D≠ → = = = → →solució única→

12 22 2 1 2

3 3 1

3

2

: 3 2 1 1 3 2 1 1 3 2 1

' 3 1 0 1 0 10 6 23 1:

2 1 1 0 5 4 12 1

F FF F F

F F F

x y z

Ax yr

m mx y mz

π→→ −

→ −

− + = − − → = ≅ − − ≅+ = − − −− + =

3 3 2

1 3 2 1 1 3 2 1

0 5 3 1 0 5 3 1 1 0 1

0 5 4 1 0 0 1 0

F F F

m m

m m

→ −− −

≅ − − ≅ − − → − = → = − − −

1m= ( ) ( )' 2 3 º . .Rang A Rang A n incògnites SC I= = < = → → ∞ →

1m≠ ( ) ( )' 3 º . .Rang A Rang A n incògnites SC D solució única= = = → → →



En la figura adjunta podem observar que si la recta r és paral·lela o està continguda en el pla aleshores el vector normal al pla , i el vector director de la recta r, seran

perpendiculars. Càlcul del vector normal a :

Càlcul del vector director de la recta r:

Estudiem ara, quan els vectors i són perpendiculars:

.

Per tant, en el cas en que tindrem que els vectors i no seran perpendiculars i per

tant la recta i el pla es tallaran en un punt. Queda per estudiar el cas . En aquest cas tenim dues possibilitats, que la recta r sigui paral·lela al pla o que la recta estigui continguda en el pla. Per decantar-nos per una o l’altra possibilitat agafarem un punt de la recta i comprovarem si pertany o no al pla.

Per trobar un punt fem per exemple , aleshores, de la 1a equació tenim que que

substituint en la 2a equació ens dóna que .

Per tant, el punt és un punt de la recta r. Comprovem ara si substituint en

l’equació de .

Per tant, amb aquest tercer mètode, com era evident, hem arribat a la mateixa conclusió que amb els altres dos, que és que: Si la recta i el pla es tallen en un punt. Si la recta està continguda en el pla. 73) PAU LOGSE 2012 Sèrie 3 Qüestió 1: Digueu per a quin valor del paràmetre m els plans , i

tenen com a intersecció una recta.

Estudiem el sistema que formen els 3 plans mitjançant el teorema de Rouché-Frobenius:

MÈTODE 1: Donat que la matriu de coeficients és quadrada el mètode més segur és fer el seu determinant. Així:

π π nπ�

rv�

π( ): 3 2 1 1, 3,2x y z nππ − + = → = −�

( ) ( )3 1: 3,1,0 2, 1, 3 1 0

2 12 1

r

i j kx y

r v mx y mz

m

+ = → = × − = = − + = −

��

�

( ) ( )3 0 2 0 3 3 5 , 3 , 5 , 3 , 5rmi k j k i mj mi mj k m m v m m= − + − + − = − − = − − → = − −� � ��

nπ�

rv�

( ) ( )1, 3,2 , 3 , 5 9 10 10 10 0 1rn v m m m m m mπ ⋅ = − ⋅ − − = + − = − = → =� �

1m≠ nπ�

rv�

1m=

13 1 3 1: :

2 1 2 1mx y x y

r rx y mz x y z

=+ = + = → − + = − + = 0x = 1y =2 0 1 1 0 1 1 2z z z⋅ − + = → − + = → =

( )0,1,2P = P π∈π

( )0,1,2: 3 2 1 0 3 1 2 2 0 3 4 1Px y z P rπ π π=− + = → − ⋅ + ⋅ = − + = → ∈ → ⊂

1m≠1m=

1 : 1x y mzπ − + = 2 : x y z mπ − + =

3 : 2 3my zπ + =

1 1 1 1

' 1 1 1

2 3 0 2 3

x y mz m

x y z m A m

my z m

− + = − − + = → = −

+ =

A



• Cas :

En aquest cas els tres plans no tenen cap punt en comú. Si ens ho demanessin caldria estudiar els plans dos a dos per acabar de decidir la seva posició relativa. • Cas :

En aquest cas els tres plans es tallen en una recta, per tant la resposta al problema és

• En el cas en que i tindríem:

Els tres plans es tallen

en un punt. MÈTODE 2: Esgraonant la matriu mitjançant el mètode de Gauss.

Una vegada esgraonada la matriu, els valors que anul·larien el determinant de A són els que

estan en la diagonal de A, per tant, cal estudiar els valors que fan que i

evidentment obtenim els mateixos valors que abans. 74) PAU LOGSE 2012 Sèrie 3 Qüestió 3:

Donats el pla i la recta

a) Calculeu el punt d’intersecció entre el pla i la recta.

( )2 2

1 1 1

1 1 3 0 0 3 0 1 0

0 3

A m m m m m m m

m

−= − = − + + − − + = − + = → ⋅ − + = →

0

1 0 1

m

m m

=→ − + = → =0m=

1 1 0 1 1 1 0 1 1 1 0 1

' 1 1 1 0 0 0 1 1 0 0 1 1

0 0 2 3 0 0 2 3 0 0 0 5

A

− − − = − ≅ − ≅ − →

( ) ( )2 3 ' . .Rang A Rang A S I→ = ≠ = →

1m=1 1 1 1 1 1 1 1

1 1 1 1' 1 1 1 1 0 0 0 0

0 1 2 30 1 2 3 0 1 2 3

A

− − − = − ≅ ≅ →

( ) ( )2 ' 3 º . . .Rang A Rang A n incògnites S C I→ = = < = →

1m=

1m≠ 0m≠( ) ( )0 ' 3 º . . .A Rang A Rang A n incògnites S C D≠ → = = = → →

112 2 2

1 1 1 1 1 1 1 1 1

' 1 1 1 0 0 1 1 0 2 3

0 2 3 0 2 3 0 0 1 1

FF F F Fm m m

A m m m m

m m m m

→ − ↔− − −

= − ≅ − − ≅ − −

( )1 1 0m m⋅ ⋅ − =

: 2 5 0x y zπ − + − =0

:2 10

x y zr

x y z

+ + = − + =



Així el punt de tall entre el pla i la recta és .

b) Trobeu l’equació contínua de la recta s continguda en el pla , que és perpendicular a la recta r i talla la recta r. MÈTODE 1: Quan donem una recta mitjançant la seva equació general en realitat l’estem donant com a intersecció de dos plans. Intentarem donar la recta s que ens demanen com a intersecció de dos plans. Com la recta s està continguda en el pla , un dels dos plans que la determinarà serà precisament el pla , per

tant, s serà de la forma: .

Per tant, el que ens queda es calcular el pla . Sabem que s ha de ser perpendicular a la recta r, aleshores si fem el pla perpendicular a r que passa pel punt d’intersecció P tindrem precisament el pla que necessitem. Així:

Com aleshores:

i per tant la recta buscada és:

2 2 1

3 3 12

2 5 0 2 5 1 1 2 5 1 1 2 5

0 0 ' 1 1 1 0 0 2 1 5

2 10 2 10 2 1 1 10 0 1 3 0

F F F

F F F

x y z x y z

x y z x y z A

x y z x y z

→ −

→ −

− + − = − + = − − + + = ≅ + + = → = ≅ − − ≅

− + = − + = − −

2 3 3 3 221 1 2 5 1 1 2 5

0 1 3 0 0 1 3 0

0 2 1 5 0 0 5 5

F F F F F↔ → −− −

≅ − ≅ − − − −

5 5 1z z= − → = −( )3 0 3 1 0 3 0 3y z y y y− = → − − = → + = → = −

2 5 3 2 5 1 5 4x y z x x x− + = → + − = → + = → =

( )4, 3, 1P = − −

π

π π: 2 5 0

:' :

x y zs

ππ

− + − =

'π

'π'' rr n vππ ⊥ → =� �

( )0: 1 1 1 2 2 2 3 2,1, 3

2 102 1 1

r r

i j kx y z

r v i k j k i j i j k vx y z

+ + =→ = = − + − + − = + − → = − − + = −

��

� � ��

( )' 2,1, 3rn vπ = = −� �

( ) ( )4, 3, 1 '' : 2 3 0 2 4 3 3 1 0 8 3 3Px y z k kππ = − − ∈+ − + = → ⋅ − − ⋅ − + = → − + 0k+ = →8 ' : 2 3 8 0k x y zπ→ = − → + − − =

: 2 5 0:

' : 2 3 8 0

x y zs

x y z

ππ

− + − = + − − =



MÈTODE 2: La recta s està continguda en el pla , per tant, el vector director de s serà

perpendicular al vector normal al pla . És a dir, .

Però també ens diuen que s ha de ser perpendicular a la recta r, per tant el vector director de s també ha de ser perpendicular al vector director de la recta r que ja hem calculat abans que és

.

Donat que el vector director ha de ser perpendicular als vectors i

podem calcular el vector com el producte vectorial d’aquests dos, és a dir:

Donat que la recta s passa pel punt tenim que:

75) PAU LOGSE 2012 Sèrie 3 Qüestió 6: Donats els punts P = (1, 0, 0), Q= (0, 2, 0), R = (0, 0, 3) i S = (1, 2, 3), a) Calculeu l’equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla que conté els punts P, Q i R. Per formar el pla necessitem un punt i dos vectors directors.

El pla que passa pel punt i té com a vectors directors i

és:

b) Comproveu si els quatre punts són coplanaris (és a dir, si els quatre estan continguts en un mateix pla). Per comprovar-ho, solament caldrà comprovar si el punt D satisfà l’equació del pla que passa pels altres tres punts:

Els quatre punts no són coplanaris.

ππ ( )1, 1,2sv nπ⊥ = −� �

( )2,1, 3rv = −�

sv� ( )1, 1,2nπ = −�

( )2,1, 3rv = −�sv�

( )1 1 2 3 4 2 2 3 7 3 1,7,3

2 1 3s s

i j k

v i k j k i j i j k v= − = + + + − + = + + → =−

��

� � ��

( )4, 3, 1P = − −

4 3 1:

1 7 3

x y zs

− + += =

( ) ( ) ( )0,2,0 1,0,0 1,2,0PQ Q P= − = − = −��

( ) ( ) ( )0,0,3 1,0,0 1,0,3PR R P= − = − = −��

( )1,0,0P = ( )1,2,0PQ = −��

( )1,0,3PR= −��

( )1 1 1

: 2 0 0 6 1 2 3 0 6 6 2 3 0

0 3

x

y x z y x z y

z

π− − −

= → − + + = → − + + = →

: 6 3 2 6 0x y zπ→ + + − =

( )1,2,3: 6 3 2 6 0 6 1 3 2 2 3 6 6 6 6 6 12 0Sx y z Sπ π=+ + − = → ⋅ + ⋅ + ⋅ − = + + − = ≠ → ∉ →



76) PAU 2012 Sèrie 3 Qüestió 6: Considereu les rectes de l’espai següents:

,

a) Comproveu que són secants. Per comprovar que efectivament les dues rectes es tallen en un punt hi ha dos mètodes, resoldre el sistema que formen o bé demostrar que si agafem un punt P de r, un punt Q de s i

construïm el vector , aleshores aquest vector, el vector director de r i el vector director de s són coplanaris. MÈTODE 1: Resolució del sistema que formen les dues rectes.

Així, les dues rectes es tallen en el punt

MÈTODE 2: Agafant un punt P de r, un punt Q de s, construint el vector i demostrant

que , el vector director de r i el vector director de s són coplanaris.

r i s es tallen en un punt

b) Calculeu l’equació contínua de la recta que les talla i que és perpendicular a totes dues.

1 1: 1

2 1

x zr y

+ −= − =−

4 1 2:

3 1 2

x y zs

− − −= =−

PQ��

12

11

1 1 2 2 2 31 1: 1

2 1 1 1 1 2 2

x

z

y x y x yx zr y

y y z z y y z

+

−−

= − → + = − → − = −+ −= − = → − − = → − + = − → = + → + =14

3 1

1 21 2

4 3 3 7 3 3 74 1 2:

3 1 2 2 2 2 2 4

yx

y z

x y y x x yx y zs

y z y z

−−−

− −−

= → − + = − → = + → + =− − − = = → − = → − = − + → + =

Restant

Restant

2 32 35 10 2 1

3 72

3 7 22 0

2 4 2 4

x yx yy y x

x yy z

x y y zy z

y z y z

− = −− = − → = → = = + =+ = → + = + = → = = + = + =

( )1,2,0

PQ��

PQ��

( )( )

1,1,11 1: 1

2 1 2,1, 1r

P rx zr y

v

= − ∈+ − = − = → − = −�

( )( )4,1,24 1 2

:3 1 2 3, 1,2s

Q sx y zs

v

= ∈− − − = = → − = −�

( ) ( ) ( )4,1,2 1,1,1 5,0,1PQ Q P= − = − − =��

5 2 3

, , 0 1 1 10 0 2 3 5 0 0

1 1 2r sPQ v v = − = + − − − − = →

−

��



Sigui la recta que busquem. Com talla a les dues rectes i , aleshores passa pel punt

de tall de i , és a dir, .

Com és perpendicular a i a , aleshores el vector director de , serà perpendicular a

i .

que si passem a la seva equació continua tenim:

77) PAU 2013 Sèrie 3 Qüestió 1: Sigui : 3 2 10x y zπ − + = .

a) Trobeu l’equació continua de la recta r perpendicular a π que passa pel punt

( )1,3,2P = − .

( ) ( )1 3 23, 2,1 :

3 2 1r r

x y zr v n v rππ

− − − −⊥ → = → = − → = = →−

� � �

1 3 2:

3 2 1

x y zr

+ − −→ = =−

b) Trobeu també l’equació cartesiana (és a dir, de la forma 0Ax By Cz D+ + + = del pla 1π

paral·lel a π que passa pel mateix punt P .

Els plans paral·lels a π tenen la forma 1 : 3 2 0x y z Dπ − + + =

( ) ( )1 11,3,2 :3 1 2 3 2 0 3 6 2 0 7 0P D D Dπ π= − ∈ → ⋅ − − ⋅ + + = → − − + + = → − + = →

17 :3 2 7 0D x y zπ→ = → − + + =


Un triangle d’àrea 3 / 2 té dos dels vèrtexs als punts ( )0,0,0P = i ( )2,0,1Q = . El

tercer vèrtex, R, és un punt de la recta 0

:1

x y zr

y

+ + = =

i té la primera coordenada

no nul·la. Calculeu les coordenades del vèrtex R.

t t r s t

r s ( )1,2,0A t= ∈t r s t tv

�

rv�

sv�

( )2 1 1 2 2 3 3 4 7 5 1, 7, 5

3 1 2t r s

i j k

v v v i k j k i j i j k= × = − = − − − − − = − − = − −−

��

� � ��

( ) ( ) ( ): , , 1,2,0 1, 7, 5t x y z λ= + − −

1 2:

1 7 5

x y zt

− −= =− −



Primer calcularem un punt genèric de la recta r . Per a aconseguir-ho hem d’expressar la recta com a suma d’un punt més el múltiple d’un vector.

:0:

1 1

1 1

1 1

zx y z x y zr

y y

x x

y y

λ

λ λ

=+ + = + = − → → = =

+ = − = − − → → → = =

( ) ( ), , 1 , 1,x y z λ λ→ = − −

Així ( )1 , 1,R λ λ= − −

Recordant que el mòdul del producte vectorial de dos vectors és l’àrea del paral·lelogram que formen i que l’àrea del triangle PQR serà la meitat de l’àrea del

paral·lelogram de costats PQ��

i PR��

tenim:

( ) ( ) ( )2,0,1 0,0,0 2,0,1PQ Q P= − = − =��

( ) ( ) ( )1 , 1, 0,0,0 1 , 1,PR R P λ λ λ λ= − = − − − = − −��

( ) ( ) ( )2,0,1 1 , 1, 2 0 1 2 1 2

1 1

i j k

PQ PR k j i jλ λ λ λλ λ

× = × − − = = + − − − − =− −

��

��

( ) ( )1 3 2 1, 1 3 , 2i j kλ λ= − + − − + = − − − →��

( ) ( ) ( )2 2 2 21, 1 3 , 2 1 1 3 2 1 1 6 9 4PQ PR λ λ λ λ→ × = − − − = − + − − + = + + + + =��

29 6 6λ λ= + +

Àrea triangle 3

2PQR= → Àrea paral·lelogram de costats PQ

�� i 3PR= →��

2 2 2 33 9 6 6 3 9 6 6 9 9 6 3 0PQ PR λ λ λ λ λ λ ÷→ × = → + + = → + + = → + − = →��

1

2 33 2 1 01

λλ λ

λ=

→ + − = → = −

( ) ( )( )

13

1

4 13 3,1,

1 , 1,0,1, 1

Rλ

λλ λ

=

=−

−→= − − → → −



Com l’enunciat diu que la primera coordenada del punt R és no nul·la, aleshores hem

de descartar la segona solució i quedar-nos amb ( )4 13 3,1,R −=

79) PAU 2013 Sèrie 4 Qüestió 5: Donats els punts i , trobeu un punt de la recta

que compleixi que el triangle de vèrtexs , i és

isòsceles, en què i són els costats iguals del triangle.

Un punt genèric de la recta seria:

Per tant:

80) PAU 2013 Sèrie 5 Qüestió 1: Siguin el pla i el pla .

a) Comproveu que els plans i són perpendiculars.

( )1,0, 1P = − ( )1,2,3Q = − R

3 4 3:

2 3 1

x y zr

+ + −= =−

P Q R

PR QR

( ) ( ) ( )

3 4 3:

2 3 1, , 3, 4,3 2,3, 1

x y zr

x y z λ

+ + −= = →−

→ = − − + −

( )3 2 , 4 3 ,3R λ λ λ= − + − + −

( ) ( ) (3 2 , 4 3 ,3 1,0, 1 4 2 , 4 3 ,4PR R P λ λ λ λ λ λ= − = − + − + − − − = − + − + −��

( ) ( ) ( )3 2 , 4 3 ,3 1,2,3 2 2 , 6 3 ,QR R Q λ λ λ λ λ λ= − = − + − + − − − = − + − + −��

( ) ( )4 2 , 4 3 ,4 2 2 , 6 3 ,PR QR λ λ λ λ λ λ= → − + − + − = − + − + − →��

( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 2 2 24 2 4 3 4 2 2 6 3 xλ λ λ λ λ λ→ − + + − + + − = − + + − + + − →

( ) ( ) ( ) ( ) ( ) ( )2 2 2 2 2 24 2 4 3 4 2 2 6 3λ λ λ λ λ λ→ − + + − + + − = − + + − + + − →

2 2 2 2 2 216 16 4 16 24 9 16 8 4 8 4 36 36 9λ λ λ λ λ λ λ λ λ λ λ→ − + + − + + − + = − + + − + + →

48 48 44 40 48 40 48 44 8 4 2λ λ λ λ λ λ→ − + = − + → − = − → = → =

( ) ( )23 2 , 4 3 ,3 1,2,1R Rλλ λ λ == − + − + − → =

1π 2 3 4x y z+ − = 2π 2 4 10x y z− − =

1π 2π



b) Trobeu l’equació continua de la recta paral·lela als plans i i que passa pel

que .

Els plans i seran perpendiculars si ho són els seus vectors normals, és a dir, si el

producte escalar dels seus vectors normals és zero.

Sigui la recta buscada. Si és paral·lela als plans i , aleshores el vector

director de serà perpendicular als vectors normals dels dos plans, és a dir:

Per tant, té la mateixa direcció que el vector que dividint-lo entre

tenim:

Aleshores és la recta que passa pel punt i té com a vector director

i per tant la seva equació continua serà:


Donats els punts , i ,

a) Trobeu l’equació cartesiana (és a dir, de la forma ) del pla que determinen.

b) Trobeu un punt pertanyent a la recta , de manera que el

tetraedre de vèrtexs , , i tinguin un volum igual a .

A partir d’aquests tres punts trobarem un punt i dos vectors.

, i

1π 2π( )1,3,2P = −

1π 2π

( )1 1: 2 3 4 2,3, 1x y z nπ + − = → = −�

( )2 2: 2 4 10 1, 2, 4x y z nπ − − = → = − −�

( ) ( )1 2 1 22,3, 1 1, 2, 4 2 6 4 0n n π π⋅ = − ⋅ − − = − + = → ⊥� �

r r 1π 2πr

( ) ( )1 2 2,3, 1 1, 2, 4 2 3 1 12 4 3 2 8

1 2 4r

i j k

v n n i k j k i j= × = − × − − = − = − − − − − + =− −

��

� ��

( )14 7 7 14,7, 7i j k= − + − = − −��

rv� ( )14,7, 7− − 7−

( )2, 1,1rv = −�

r ( )1,3,2P = −

( )2, 1,1rv = −�

1 3 2:

2 1 1

x y zr

+ − −= =−

( )1, 1,2P = − ( )2,0,1Q = ( )3,2, 1R= −0Ax By Cz D+ + + =

S5 1 5

:2 1 3

x y zr

− − −= =− −

P Q R S 1/ 2

( )1, 1,2P = − ( )2,0,1Q = ( )3,2, 1R = −

( ) ( ) ( )2,0,1 1, 1,2 1,1, 1PQ Q P= − = − − = −��

( ) ( ) ( )3,2, 1 1, 1,2 2,3, 3PR R P= − = − − − = −��



El volum del tetraedre format per 4 punts és la sisena part del volum del paral·lelepípede que determinen. El volum d’aquest paral·lelepípede es pot calcular com el valor absolut del producte mixt dels 3 vectors amb origen comú que formen els 4 punts.

Un punt genèric de la recta és:

Per tant, tenim els punts: , , i

Que formen els vectors amb origen comú en :

Per tant, hi ha dos punts amb les condicions del problema:


Considereu els punts i .

a) Trobeu l’equació del pla format per tots els punts que equidisten de i . b) Donat un punt , dividim el segment en tres parts iguals i obtenim

els punts , i . Trobeu el punt .

( ) ( ) ( ) ( ) ( ) ( )1 1 2

: 1 1 3 0 3 1 2 1 3 2 2 2 3 1 3 1 0

2 1 3

x

y x y z z x y

z

π−+ = → − − − + + − − − + − + + = →− − −

( ) ( )1 2 0 1 0y z y z→ + + − = → + − =

5 1 5:

2 1 3

x y zr

− − −= =− −

( ) ( ): , , 5 2 ,1 ,5 3S x y z λ λ λ= + − −

( )1, 1,2P = − ( )2,0,1Q = ( )3,2, 1R = − ( )5 2 ,1 ,5 3S λ λ λ= + − −P

( ) ( ) ( )2,0,1 1, 1,2 1,1, 1PQ Q P= − = − − = −��

( ) ( ) ( )3,2, 1 1, 1,2 2,3, 3PR R P= − = − − − = −��

( ) ( ) ( )5 2 ,1 ,5 3 1, 1,2 4 2 ,2 ,3 3PS S P λ λ λ λ λ λ= − = + − − − − = + − −��

1 2 4 2

, , 1 3 2

1 3 3 3

PQ PR PS

λλλ

+ = − =

− − −

��

( ) ( ) ( ) ( ) ( ) ( )3 3 3 3 4 2 2 2 3 4 2 3 2 2 3 3λ λ λ λ λ λ= − − + − − + + + − − − =

( ) ( )3 3 2 5 4λ λ λ= − + − = −

61· 3 , , 3

2xVolum tetaedre Volum paral lelepípede PQ PR PS = → = → = →

��

125 4 3 2 4

5 4 3 5 4 35 4 3 8 4 2

λ λ λλ λ

λ λ λ− = → = → =

→ − = → − = ± → − = − → = → =

S

( ) ( )12

71 1 1 11 12 2 2 2 25 2 ,1 ,5 3 6, ,S S

λ =

= + ⋅ − − ⋅ → =

( ) ( )2

2 25 2 2,1 2,5 3 2 9, 1, 1S Sλ == + ⋅ − − ⋅ → = − −

( )1,2,4A= − ( )3,0, 2B = −A B

( ), ,C x y z= AC

,A 1A B C C



El punt mitjà del segment serà:

El pla buscat serà el pla que passa per i

té com a vector normal el vector , per

tant:

D’acord amb el dibuix tenim:


Donats el pla : 2 3x y zπ + − = i la recta 1

:2 4

x z mr y

− += = ,

a) Comproveu que el vector característic (o normal) de π i el vector director de són perpendiculars.

b) Estudieu la posició relativa de i en funció del paràmetre m. El vector normal al pla : 2 3x y zπ + − = és ( ): 1,2, 1nπ = −�

mentre que el vector

director de la recta 1

:2 4

x z mr y

− += = és ( )2,1,4rv =� .

Aquests vectors seran perpendiculars sii el seu producte escalar és zero. ( ) ( )1,2, 1 2,1,4 2 2 4 0rn v n vπ ⋅ = − ⋅ = + − = → ⊥� � � �

El fet de que nπ

� i rv�

siguin perpendiculars fa que el pla

π i la recta r solament puguin ser o bé paral·lels o

( ) ( ) ( )3,0, 2 1,2,4 4, 2, 6AB B A= − = − − − = − −��

AB

( ) ( )( ) ( ) ( )

1 11,2,4 4, 2, 6

2 21,2,4 2, 1, 3 1,1,1

ABM A AB= + = − + − − =

= − + − − =

��

( )1,1,1ABM =

( )4,0, 6AB= −��

( )1,1,1: 4 0 6 0 4 6 0 4 1 6 1 0x y z D x z D Dππ ∈+ − + = → − + = → ⋅ − ⋅ + = →24 6 0 2 0 2 : 4 6 2 0D D D x zπ ÷→ − + = → − + = → = → − + = →

: 2 3 1 0x zπ→ − + =

( ) ( )

( ) ( ) ( )

3 31,2,4 4, 2, 6

2 2

1,2,4 6, 3, 9 5, 1, 5

C A AB= + = − + − − =

= − + − − = − −

��

rπ r



que la recta estigui continguda en el pla tal i com es pot apreciar en el dibuix adjunt. Donat que el paràmetre m no influeix en el vector de la recta per a qualsevol valor de m solament hi haurà les dos possibilitats anteriors, és a dir, que la recta sigui paral·lela al pla o que hi estigui continguda. Sigui ( )1,0,A m= − un punt de la recta r . Aleshores si A π∈ la recta estarà

continguda en el pla i si A π∉ aleshores serà paral·lela. Substituint el punt A en l’equació del pla π tenim que

( )1 2 0 1 0 1 3 2m m m m+ ⋅ − − = + + = + = → =

Per tant, Si 2m= aleshores la recta r està continguda en el pla π mentre que Si 2m≠ aleshores la recta r és paral·lela a π . NOTA: També podíem treballar per rangs arribant com és evident al mateix resultat.

11 2 2 1

2 11 2:42 4

4 44

xy x y x y

x yx z mr y

z m y z my y z m y z m

− = → − = → − = − =− + = = → → + − = = → = + → − =

2 2 1

: 2 3 2 3 1 2 1 3 1 2 1 3

2 1 1 2 0 1 0 4 1 22 1:

4 0 4 1 0 4 14

F F Fx y z x y z

x yx yr

y z m m my z m

π→ −

+ − = + − = − − ≅ − = ≅ − ≅ − − ≅− = − = − −− =

2 3 3 3 2

1 2 1 3 1 2 1 3

0 4 1 0 4 1

0 4 1 2 0 0 0 2

F F F F F

m m

m

↔ → +− −

≅ − ≅ − − − −

2 0 2m m− = → =

• ( ) ( )2 ' 2 3 º . .I.m Rang A Rang A n incògnites S C= → = = < = → amb un grau de

llibertat → la recta r i el pla π tenen una recta en comú r π→ ⊂ . • ( ) ( )2 2 3 ' . .m Rang A Rang A S I r≠ → = ≠ = → → i π no tenen cap punt en comú

r π→ � . 84) PAU 2013 Sèrie 1 Qüestió 5: Donats el pla : 2 3 8 0x y zπ − + − = i el punt ( )6, 3,7P = − ,

a) Trobeu l’equació contínua de la recta que passa per P i és perpendicular a π . b) Trobeu el punt del pla π que està més proper al punt P .



Sigui r la recta buscada. Per ser perpendicular a π tindrem que el vector director de r coincidirà amb el vector normal al pla π , és a dir: ( )2, 1,3rv nπ= = −� �

.

Per tant la recta r serà la recta que passa pel punt ( )6, 3,7P = − i té com a vector

director ( )2, 1,3rv = −� és a dir:

6 3 7:

2 1 3

x y zr

− + −= =−

Òbviament el punt del pla π que està més proper a P serà la intersecció entre el pla π i la recta r . Aquest punt l’anomenarem Q. Així, per trobar el nostre punt Q solament hem de resoldre el sistema format per la recta i el pla.

6 36 2 6

26 3 7 2 1: :3 7 3 22 1 3

3 9 71 3

x yx y

x yx y zr r

y z y zy z

− + = → − + = + − =− + − −= = → → + − + = −− = → + = − + −

2 1 2 0 0 1 2 0 0

: 3 2 0 3 1 2 0 3 1 2

2 3 8 0 2 1 3 8 0 5 3 8

x y

r y z

x y z

π− = ∩ + = − → − ≅ − ≅ − + − = − −

1 2 0 0 1 2 0 0

0 15 5 10 0 15 5 10

0 15 9 24 0 0 14 14

≅ − ≅ − −

14 14 1z z= → = 3 2 3 1 2 3 3 1y z y y y+ = − → + = − → = − → = −

( )2 0 2 1 0 2 0 2x y x x x+ = → + ⋅ − = → − = → =

Per tant, ( )2, 1,1Q = − .

85) PAU 2014 Sèrie 3 Qüestió 2: Considereu el punt ( )1,2,3A = .

a) Calculeu el punt simètric del punt A respecte de la recta d’equació ( ) ( ): , , 3 , 1, 3r x y z λ λ= + − .

• Calculem el pla π perpendicular a la recta r i que passa pel punt A.

( ) ( ) ( ): , , 3 , 1, 3 1,0, 1rr x y z vλ λ= + − → = −�

Per ser perpendicular a r , aquest pla π tindrà com a vector normal el vector director de r . És a dir, ( )1,0, 1 :1 0 1 0 : 0rn v x y z D x z Dπ π π= = − → + − + = → − + = →� �



( )1,2,3A π= ∈→ 1 3 0 2 : 2 0D D x zπ− + = → = → − + = • Calculem el punt de tall entre r i π :

( ) ( ) 0 1 13 1 3: , , 3 , 1, 3 : :

3 3 6 01 0 1

y yx y zr x y z r r

x z x zλ λ

= − → =− − −= + − → = = → − + = − → + − =− Així el sistema format per r i π és:

1 1

6 0 6

2 0 2

y y

x z x z

x z x z

= = + − = ≅ + = − + = − = −

Sumant les dues últimes equacions tenim

2 4 2 4x x z= → = → = Per tant el pla π i la recta r es tallen en el punt ( )2,1,4P = .

• Finalment el simètric de A respecte de r serà 'A P AP= +

��.

( ) ( ) ( )2,1,4 1,2,3 1, 1,1AP P A= − = − = −��

( ) ( ) ( )' 2,1,4 1, 1,1 ' 3,0,5A P AP A= + = + − → =��

b) Calculeu el punt simètric del punt A respecte del pla que té per equació

: 3x y zπ + + = .

• Calculem l’equació de la recta r perpendicular al pla π i que passa pel punt A.

( )( ) ( ) ( )

1,1,1

: , , 1,2,3 1,1,1

A rr rr v n v

r x y z

ππλ

∈⊥ → = → = →

= +

� � �

• Calculem el punt de tall entre r i π . Un punt genèric de r és ( )1, 2, 3P λ λ λ= + + + .

Si obliguem a que aquest punt pertany també a π tenim: ( ) ( ) ( )1 2 3 3 3 6 3 3 3 1λ λ λ λ λ λ+ + + + + = → + = → = − → = − →

( ) ( )1 1, 1 2, 1 3 0, 1, 2P P→ = − + − + − + → =

• Finalment el simètric de A serà 'A P AP= +

��.

( ) ( ) ( )0, 1, 2 1, 2, 3 1, 1, 1AP P A= − = − = − − −��

( ) ( ) ( )' 0,1,2 1, 1, 1 ' 1,0,1A P AP A= + = + − − − → = −��




Siguin r i s les rectes de 3ℝ d’equacions

2 1:

3 4

x zr y

− += = i

( ) ( ): , , 1 2 , 3 , 4 3s x y z α α α= + − + , amb α ∈ℝ .

a) Comproveu que els punts mitjans dels segments que tenen un extrem situat sobre la recta r i l’altre extrem situat sobre la recta s formen un pla.

( ) ( ) ( )2 1: : , , 2,0, 1 3,1,4

3 4

x zr y r x y z µ− += = → = − + Per tant un punt genèric de r

serà ( )2 3 , , 1 4P µ µ µ= + − +

( ) ( ): , , 1 2 , 3 , 4 3s x y z α α α= + − + → Un punt genèric de s serà

( )1 2 , 3 , 4 3Q α α α= + − + .

Per calcular el punt mitjà d’aquest segment PQ��

sumem els punts i dividim el resultat

entre 2, és a dir: ( ) ( )2 3 , , 1 4 1 2 , 3 , 4 3

2 2PQ

P QM

µ µ µ α α α+ − + + + − ++= = =

( )3 3 2 , 3 , 3 4 3 3 3 3 3 1 1 3, , , , 2 1, ,

2 2 2 2 2 2 2 2

µ α µ α µ αµ α

+ + + − + + = = + + −

Multiplicant els vectors per 2 per tal d’evitar denominadors, tenim que els punts mitjans dels segments formats amb un extrem en la recta r i l’altre extrem en la recta s són:

( ) ( )3 3 3, , 3, 1, 4 2, 1, 3

2 2 2PQM µ α = + + −

, per tant aquests punts formen el pla

que passa pel punt 3 3 3

, ,2 2 2

i té com a vectors directors ( )3,1,4u =� i ( )2, 1,3v = −�.

Evidentment és un pla perquè els vectors u�

i v�

són linealment independents perquè 3 1

2 1≠

−.

b) Trobeu l’equació general (és a dir, que té la forma Ax By Cz D+ + = ) del pla de l’apartat anterior.

( ) ( )

33 2

23 3 3 3

: , , 3, 1, 4 2, 1, 3 : 1 1 02 2 2 2

34 3

2

x

y

z

π µ α π

−

+ + − → − − = →

−

3 3 3 3 3 33 8 3 2 4 9 0

2 2 2 2 2 2x y z z x y → ⋅ − + ⋅ − − ⋅ − − ⋅ − + ⋅ − − ⋅ − = →



3 3 3 21 3 157 5 0 7 5 0

2 2 2 2 2 2x y z x y z → ⋅ − − − − ⋅ − = → − − + − + = →

23

7 5 0 :14 2 10 3 02

xx y z x y zπ→ − − − = → − − − =

87) PAU 2014 Sèrie 4 Qüestió 3: Siguin els punts ( )1,1,0P = , ( )1,0,1Q = i ( )0,1,1R = i el pla : 4x y zπ + + = .

a) Trobeu l’equació general (es a dir, que té la forma Ax By Cz D+ + = ) del pla que passa pels punts P, Q i R. Per determinar un pla 'π necessitem un punt i dos vectors directors. Podem calcular el pla 'π que passa pels punts P, Q i R com el pla que passa per P i té com a vectors

directors PQ��

i PR��

.

( ) ( ) ( )1,0,1 1,1,0 0, 1,1PQ Q P= − = − = −��

( ) ( ) ( )0,1,1 1,1,0 1,0,1PR R P= − = − = −��

1 0 1

' : 1 1 0 0

0 1 1

x

y

z

π− −− − = →−

( ) ( ) ( ) ( ) ( ) ( )' : 1 1 1 1 0 0 1 0 0 1 0 1 0x y z z x yπ→ − − − − + − − − − − − − = →

( ) ( ) ( )' : 1 1 1 1 1 0 0 ' : 1 1 0x y z x y zπ π→ − − − − − − = → − + − + − = →

( )1' : 2 ' : 2xx y z x y zπ π−→ − − − = − → + + =

b) Si S és un punt de π , comproveu que el volum del tetraedre de vèrtexs P, Q, R i S no depèn del punt S. El volum del tetraedre de vèrtexs P, Q, R i S és la sisena part del volum del paral·lelepípede de costats PQ, PR i PS . Per altra banda sabem que el volum d’aquest paral·lelepípede coincideix amb el valor absolut del producte mixt dels vectors PQ

��, PR��

i PS��

. Sigui S un punt genèric del pla : 4x y zπ + + = , aleshores S serà de la forma

( ), ,4S x y x y= − − i per tant:

( ) ( ) ( )1,0,1 1,1,0 0, 1,1PQ Q P= − = − = −��

( ) ( ) ( )0,1,1 1,1,0 1,0,1PR R P= − = − = −��

( ) ( ) ( ), ,4 1,1,0 1, 1, 4PS S P x y x y x y x y= − = − − − = − − − −��



Finalment:

( ) ( ) ( )0 1 1

1 1 1, , 1 0 1 1 1 1 1 1 4

6 6 61 1 4

x

V PQ PR PS y x y x y

x y

− − = ⋅ = ⋅ − − = ⋅ − − − − − − − =

− −

��

1 1 1 2 1

1 1 4 2 26 6 6 6 3

x y x y= ⋅ − + − + − + + = ⋅ − = ⋅ = =

Com podem observar el volum del tetraedre sempre és 1

3 i no depèn del punt S triat.

NOTA: També podem calcular el volum del tetraedre de vèrtexs P, Q, R i S mitjançant la fórmula del volum d’una piràmide. El volum d’una piràmide és un terç de l’àrea de la base per l’altura. Si considerem com a base de la piràmide el triangle de vèrtexs P, Q i R que pertanyen al pla 'π , el volum del tetraedre seria l’àrea del triangle PQR per l’altura del tetraedre. Una manera de veure que el volum de la piràmide és fix i no depèn de l’elecció del punt S de π seria demostrar que els plans 'π i π són paral·lels, així l’altura del tetraedre no dependria de l’elecció de S. Però el paral·lelisme entre els dos plans és evident perquè ' : 2x y zπ + + = i

: 4x y zπ + + = , per tant, ( )' 1,1,1nπ =� i ( )1,1,1nπ =� . Així els plans 'π i π tenen el

mateix vector normal i per tant són paral·lels. 88) PAU 2014 Sèrie 4 Qüestió 4: Donats els plans 1 : 4 2 1x y z mπ − + = − i ( )2 : 2 2 2 2 3 1x m y z mπ − + + = + ,

a) Determineu els valors de m perquè els plans 1π i 2π s’intersequin en una recta i

calculeu un vector director de la recta resultant que no depengui de m. Dos plans s’intersequen en una recta sii el sistema que formen les seves equacions és compatible determinat amb un grau de llibertat. Considerem la matriu ampliada del sistema:

2 2 121 4 1 2 1 1 4 1 2 1'

2 2 2 2 3 1 0 2 6 0 3

F F Fm mA

m m m m

→ −− − − − = ≅ − − + − + − +

2 6 0 2 6 3m m m− + = → = → =

Noteu que: • Si 3m= tota la segona fila es converteix en zeros i aleshores

( ) ( )' 1Rang A Rang A= = i el sistema és compatible indeterminat amb dos graus de

llibertat, és a dir, el sistema format pels dos plans té tot un pla de solucions i per tant el que està passant és que en aquest cas els dos plans són el mateix.



• Si 3m≠ aleshores ( ) ( )' 2 3 ºRang A Rang A n incògnites= = < = → Sistema

Compatible Indeterminat amb un grau de llibertat, per tant, en aquest cas els dos plans tenen una recta en comú, és a dir s’intersequen en una recta. Així la resposta a

aquest apartat és 3m≠

El vector director de la recta que defineixen dos plans és perpendicular a cadascun dels vectors normals d’aquests plans, per tant, es pot calcular com el producte vectorial dels vectors normals a 1π i 2π .

( )1 1: 4 2 1 1, 4,1x y z m nπ − + = − → = −�

( ) ( )2 2: 2 2 2 2 3 1 2, 2 2, 2x m y z m n mπ − + + = + → = − −�

( ) ( )1 2 1, 4,1 2, 2 2, 2 1 4 1

2 2 2 2r

i j k

v n n m

m

= × = − × − − = − =− −

��

� � �

( ) ( ) ( ) ( )8 2 2 2 8 2 2 2 2 6 0 2 6i m k j k m i j m i j m k= − + − − + + + + − = − + + − + =� � ��

( ) ( )(*)

2 6, 0, 2 6 1, 0, 1m m= − − + ≅ −

(*) Com estem en el cas en que 3m≠ aleshores 2 6 0m− ≠ i podem dividir tot el vector per 2 6m− .

Per tant la solució al problema és ( )1,0, 1rv = −�

b) Sigui el pla : 3 2 3 8x y zπ − + = . Estudieu la posició relativa del pla π amb la recta

r definida per la intersecció dels plans 1π i 2π quan 1m= .

( ): 3 2 3 8 3, 2,3x y z nππ − + = → = −�

( ) ( )1,0, 1 3, 2,3 3 0 3 0r rv n v nπ π⋅ = − ⋅ − = − − = → ⊥ →� � � � r és paral·lela a π o r està

continguda en π . Per distingir en quin dels dos casos ens trobem agafem un punt de r i comprovem si aquest punt pertany a π . Si en les equacions de r , fem per exemple 0x = :

2 2 12 11 4 1 2 1 1 4 1 2 1'

2 2 2 2 3 1 0 2 6 0 3

F F F mm mA

m m m m

→ − =− − − − = ≅ ≅ − − + − + − +

0

130 4 1

1 4 1 1 4 1 2: 10 4 0 2 4 2 1

22

x

zzx y z

ry y

y

=

=− ⋅ + = − − + = ≅ → → → = = =



Per tant un punt de la recta r és 1

0, , 32

P =

. Substituint en l’equació de

: 3 2 3 8x y zπ − + = tenim 1

3 0 2 3 3 0 1 9 82

P rπ⋅ − ⋅ + ⋅ = − + = → ∈ → està

continguda en π . NOTA: Una altra manera de resoldre el problema és la següent: r és la recta intersecció dels plans 1 : 4 2 1x y z mπ − + = − i

( )2 : 2 2 2 2 3 1x m y z mπ − + + = + quan 1m= .

La matriu ampliada del sistema format per 1π i 2π és:

2 2 12 11 4 1 2 1 1 4 1 2 1 1 4 1 1'

2 2 2 2 3 1 0 2 6 0 3 0 4 0 2

F F F mm mA

m m m m

→ − =− − − − − = ≅ ≅ − − + − + − +

Si ara volem intersecar la recta anterior amb el pla : 3 2 3 8x y zπ − + = l’únic que hem de fer és afegir al sistema l’equació del pla, és a dir, obtenim el sistema:

12 23 3 1 2 32

13 35

31 4 1 1 1 4 1 1 1 4 1 1

1 4 1 1' 0 4 0 2 0 4 0 2 0 2 0 1

0 2 0 13 2 3 8 0 10 0 5 0 2 0 1

F FF F F F F

F FA

→→ − =

→

− − − − = ≅ ≅ ≅ →

−

( ) ( )' 2Rang A Rang A→ = = → La recta r i el pla π formen un sistema compatible

indeterminat amb un grau de llibertat, és a dir, r i π tenen una recta en comú r→ està continguda en π . 89) PAU 2014 Sèrie 5 Qüestió 1: Siguin r i s les rectes de 3

ℝ que tenen les equacions següents: 3

: 5 52

zr x y

−+ = − = i 3 2 1

:2 3 1

x y zs

− − += =−

a) Estudieu el paral·lelisme i la perpendicularitat entre les rectes r i s.

3 5 5 3

: 5 5 :2 1 1 2

z x y zr x y r

− + − −+ = − = → = =

Els vectors directors de les rectes són ( )1,1,2rv =� i ( )2,3, 1sv = −�

• Paral·lelisme: 1 1

2 3≠ → rv

� i sv�

no proporcionals r→ i s no són paral·leles

• Perpendicularitat: ( ) ( )1,1,2 2,3, 1 2 3 2 3 0r sv v r⋅ = ⋅ − = + − = ≠ →� �

i s no són perpendiculars

b) Trobeu l’equació general (és a dir, que té la forma 0Ax By Cz D+ + + = ) del pla π que

conté la recta r i és paral·lel a la recta s . Calculeu la distància entre la recta s i el pla π obtingut.



Si el pla π conté a la recta r aleshores el punt ( )5,5,3A = − de r també serà un punt

de π i el vector director de r , ( )1,1,2rv =� serà un vector director de π .

Si el pla π és paral·lel a la recta s, aleshores el vector director de s, ( )2,3, 1sv = −�

també serà vector director de π . Per tant, π és el pla que passa pel punt ( )5,5,3A = − i té com a vectors directors

( )1,1,2rv =� i ( )2,3, 1sv = −�.

( ) ( ) ( ) ( ) ( ) ( )5 1 2

: 5 1 3 0 5 4 5 3 3 2 3 6 5 1 5 0

3 2 1

x

y x y z z x y

z

π+− = → − + + − + − − − − + + − = →− −

( ) ( ) ( )7 5 5 5 1 3 0 7 35 5 25 3 0x y z x y z→ − + + − + − = → − − + − + − = →

7 5 63 0 : 7 5 63x y z x y zπ→ − + + − = → − + + =

Com que la recta s és paral·lela al pla π la distància entre s i π serà igual a la distància entre qualsevol punt sP de s i π .

( )3 2 1: 3,2, 1

2 3 1 s

x y zs P s

− − += = → = − ∈−

( ) ( ) ( )( )( )2 2 2

7 3 5 2 1 63, , 3,2, 1 , 7 5 63 0

7 5 1sd s d P d x y zπ π

− ⋅ + ⋅ − −= = − − + + − = = =

− + +

21 10 1 63 75 75 75 7575 5 3

7549 25 1 75 75

− + − − −= = = = = =

+ +




Sigui r la recta de l’espai que té per equació 1 3

:2 1

x yr z

− += =−

i sigui P el punt de

coordenades ( )6,0, 1− .

a) Trobeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla que passa

pel punt P i talla perpendicularment la recta r .

Anomenem π al pla buscat:

( ) ( )6,0, 12, 1,1 : 2 0rPr n v n x y z D π

π ππ π = − ∈⊥ → = → = − → − + + = →� � �

12 0 1 0 11 0 11 : 2 11 0D D D x y zπ→ − − + = → + = → = − → − + − =

b) Trobeu l’equació paramètrica del pla que passa pel punt P i conté la recta r .

La recta r passa pel punt ( )1, 3,0Q = − i té com a vector director ( )2, 1,1rv = −�

Sigui 'π el pla buscat. Com 'π conté la recta r aleshores el vector rv�

serà vector

director de 'π i el punt Q també serà un punt de 'π .

Però si els punts P i Q són de 'π aleshores el vector PQ��

serà vector director de 'π.

( ) ( ) ( )1, 3,0 6,0, 1 5, 3,1PQ Q P= − = − − − = − −��

.

Finalment calculem l’equació del pla 'π com el pla que passa pel punt ( )6,0, 1P = − i té

com a vectors directors ( )2, 1,1rv = −� i ( )5, 3,1PQ = − −��

, per tant:

( ) ( ) ( ) ( )' : , , 6,0, 1 2, 1,1 5, 3,1x y zπ λ µ= − + − + − −


Considereu a 3ℝ la recta que té per equació ( ) ( ): , , 4 2 , 2,1r x y z λ λ= − + − − i els

plans 1π i 2π d’equacions 1 : 2 2 1x y zπ + + = − i 2 : 2 2 3x y zπ − + = − , respectivament.

a) Determineu la posició relativa de 1π i 2π .

1 1: 2 2 1 : 2 2 1 0x y z x y zπ π+ + = − → + + + =

2 2: 2 2 3 : 2 2 3 0x y z x y zπ π− + = − → − + + =

1

1 2

1 2n≠ →

−�

i 2n�

no proporcionals 1n→ � i 2n�

no paral·lels 1π→ i 2π es tallen en

una recta.



b) Comproveu que tots els punts de la recta r estan situats a la mateixa distància dels plans 1π i 2π .

NOTA: Podeu calcular la distància d’un pont de coordenades ( )0 0 0, ,x y z al pla


2 2 2

Ax By Cz D

A B C

+ + +

+ +

Hem d’agafar un punt genèric de la recta r i comprovar que la distància d’aquest punt a cadascun dels plans és la mateixa.

( ) ( ): , , 4 2 , 2,1r x y z λ λ= − + − − → Un punt genèric P de la recta r és

( )4 2 , 2,1P λ λ= − + − − .

( ) ( ) ( )1 2 2 2

4 2 2 2 2 1 1 4 2 4 2 2 1 5 5,

31 4 4 91 2 2d P

λ λ λ λπ

− + + − + − + − + − + − + −= = = =

+ ++ +

( ) ( ) ( )( )

2 22 2

4 2 2 2 2 1 3 4 2 4 2 2 3 5 5,

31 4 4 91 2 2d P

λ λ λ λπ

− + − − + − + − + + + − += = = =

+ ++ − +

92) PAU 2015 Sèrie 4 Qüestió 3: Siguin el punt ( )2,0,2P = i el pla π d’equació 1x y z− + = .

a) Calculeu l’equació paramètrica de la recta que passa pel punt P i és perpendicular al pla π.

Sigui r la recta buscada. ( )1, 1,1r rr v n vππ⊥ → = → = −� � �

Per tant, la recta buscada és:

( ) ( ) ( )2 1 2

: , , 2,0,2 1, 1,1 : 0 1 :

2 1 2

x x

r x y z r y r y

z z

λ λλ λ λ

λ λ

= + = + = + − → = − → = − = + = +

b) Calculeu la distància del punt P al pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

: 1 : 1 0x y z x y zπ π− + = → − + − =



( )( )

0 0 0

2 2 2 22 2

1 2 1 0 1 2 1 2 0 2 1 3 3, 3

1 1 1 3 31 1 1

Ax By Cz Dd P

A B Cπ

+ + + ⋅ − ⋅ + ⋅ − − + −= = = = = =

+ ++ + + − +

93) PAU 2015 Sèrie 4 Qüestió 6: Siguin a 3

ℝ el punt ( )2,3,3P = i la recta ( ) ( ) ( ): , , 1,2,3 1,1,1r x y z t= + .

a) Calculeu l’equació paramètrica del pla que passa pel punt P i conté la recta r .

Sigui ( )1,2,3A r= ∈

Sigui π el pla que ens demanen. Com π conté la recta r aleshores el punt A π∈ i

per tant com que P també pertany a π podem assegurar que el vector AP��

és un vector director de π . Així podem calcular el pla π com el pla que passa pel punt

( )2,3,3P = i té com a vectors directors ( )1,1,1rv =� i

( ) ( ) ( )2,3,3 1,2,3 1,1,0AP P A= − = − =��

. Així:

( ) ( ) ( ) ( ) ( ): , , 2,3,3 1,1,1 1,1,0 : 2 , 3 , 3x y zπ λ µ π λ µ λ µ λ= + + → + + + + +

b) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla que passa pel punt P i és perpendicular a la recta r . Sigui π el pla demanat. Com que rπ ⊥ aleshores ( )1,1,1rn vπ = =� �

Per tant π és de la forma 1 1 1 0x y z D+ + + = Finalment com que π passa pel punt P tenim que P π∈ i així:

( )2,3,3 : 0 2 3 3 0 8P x y z D D Dπ= ∈ + + + = → + + + = → = − →

: 8 0 : 8x y z x y zπ π→ + + − = → + + =

94) PAU 2015 Sèrie 5 Qüestió 2: A l’espai tridimensional considereu la recta ( ) ( ): , , 3 2 , , 3r x y z α α α= + − − i els plans

1 : 1x y zπ + + = − i ( ) ( )2 : , , 2 ,1 ,x y zπ λ λ µ µ= + − + .

a) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = del pla 2π

( ) ( ) ( ) ( ) ( ) ( )2 : , , 2 ,1 , , , 2,1,0 1, 1,0 0,1,1x y z x y zπ λ λ µ µ λ µ= + − + → = + − + →

( ) ( )2 1 0

: 1 1 1 0 1 2 1 1 0 2 1 0

0 1

x

y x z y x z y

z

π−

→ − − = → − − + − − = → − + + − + = →

( )123 0 : 3 0xx y z x y zπ−→ − − + + = → + − − =



b) Trobeu els dos punts de la recta r que equidisten dels plans 1π i 2π .

NOTA: Podeu calcular la distància d’un punt de coordenades ( )0 0 0, ,x y z al pla


2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Un punt genèric de la recta ( ) ( ): , , 3 2 , , 3r x y z α α α= + − − serà

( )3 2 , , 3P α α α= + − − .

Calculem la distància d’aquest punt als dos plans 1 : 1 0x y zπ + + + = i

2 : 3 0x y zπ + − − = :

( ) ( ) ( ) ( )1 2 2 2

1 3 2 1 1 3 1 3 2 3 1 7 7,

1 1 1 3 31 1 1d P

α α α α α απ

⋅ + + ⋅ − + ⋅ − + + − + − += = = =

+ ++ +

( ) ( ) ( ) ( )( )

2 22 2

1 3 2 1 1 3 3 3 2 3 3 2 3,

1 1 1 31 1 1d P

α α α α α α απ

⋅ + + ⋅ − − ⋅ − − + − − + − −= = =

+ ++ + −

( ) ( )13

2

2 37, , 7 2 3 2 3 7

3 3xd P d P

απ π α α

−= → = → = − → − = ± →

( )3 2 , , 32 3 7 2 7 3 2 10 5

2 3 7 2 7 3 2 4 2P α α αα α α α

α α α α= + − −− = = + = =

→ → → → → − = − = − + = − = −

( )

( )

13, 5, 2

1,2,5

P

P

= − −

→ = −

95) PAU 2015 Sèrie 5 Qüestió 4: Siguin els plans de 3

ℝ 1 : 2y zπ − + = , 2 : 2 1x y zπ − + + = i 3 : 2 2 1x zπ − = − .

a) Calculeu la posició relativa dels tres plans. • Primer estudiarem les solucions del sistema format pels tres plans:

1 3 2 2 1

2 0 1 1 2 2 0 2 1

2 1 2 1 1 1 2 1 1 1

2 2 1 2 0 2 1 0 1 1 2

F F F F Fy z

x y z

x z

↔ → +− + = − − − − + + = ≅ − ≅ − ≅ − = − − − −

3 3 2

2 0 2 1 2 0 2 1

0 1 1 0 0 1 1 0

0 1 1 2 0 0 0 2

F F F→ +− − − −

≅ − ≅ − → −



( ) ( )2 3 ' . .Rang A Rang A S I→ = ≠ = → → Els tres plans no tenen cap punt en comú.

• Ara estudiem la existència de plans paral·lels:

1 2

0 1

2 1iπ π−≠ →

− no són paral·lels

1 3

0 1

2 0iπ π−≠ → no són paral·lels

2 3

2 1

2 0iπ π− ≠ → no són paral·lels

Per tant no hi ha cap parell de plans paral·lels i estem en el cas 7, els plans es tallen dos a dos. En la figura de la dreta hem representat els plans.

b) Comproveu que el pla 3π és paral·lel a la recta definida per la intersecció dels plans

1π i 2π .

Calculem primer l’equació vectorial de la recta intersecció de 1π i 2π .

1

2

:: 2 2 2 2

: 2 1 2 1 2 1 2 1zy z y z y z y

x y z x y z x y z x yλπ λ

π λ=− + = − = − = − = −

≅ ≅ → − + + = − + = − − + = − − + = −

2 3 2 2 3

2 1 2 2 1 2 3 22 2

yx y x x x xλ λ λλ λ λ λ= − − −− + = − →− + − = − → − = − → = → =−

Per tant: ( ) ( ) ( )2 3 3, , , 2, , , , 2,0 1,1,1

2 2x y z x y z

λ λ λ λ− − = − → = − +

Així la intersecció dels plans 1π i 2π és la recta que passa pel punt 3

, 2,02

A− = −

i té

com a vector director ( )1,1,1v =� .

Finalment per comprovar que el pla 3π és paral·lel a aquesta recta demostrarem que

v�

és ortogonal al vector normal de 3π i que el punt A no pertany a aquest pla.

( ) ( )3 33 : 2 2 1 2,0, 2 1,0, 1x z n nπ ππ − = − → = − → −� �

≃

( ) ( )3 3

1,1,1 1,0, 1 1 0 1 0v n v nπ π⋅ = ⋅ − = + − = → ⊥� � � �

?

3

3, 2,0

2A π− = − ∈

3

32 2 0 3 0 3 1

2A π−⋅ − ⋅ = − − = − ≠ − → ∉ i per tant la recta és paral·lela a aquest pla.



96) PAU 2016 Sèrie 1 Qüestió 1: Siguin la recta r: (x, y, z) = (5 + k, k, –2 – 2k) i els punts P = (1, 0, –1) i Q = (2, 1, 1). a) Calculeu l’equació paramètrica de la recta que passa pel punt Q i és perpendicular al pla determinat per la recta r i el punt P.

• En primer lloc calcularem el pla determinat per la recta r i el punt P. Per determinar aquest pla que anomenarem π necessitem un punt i dos vectors directors. Com que el vector director de la recta r és ( )1,1, 2rv = −�

aleshores aquest vector

també serà vector director del pla. Com que el punt ( )5,0, 2R = − és un punt de la recta r també serà un punt del pla π

i per tant el vector ( ) ( ) ( )1,0, 1 5,0, 2 4,0,1RP P R= − = − − − = −��

serà un vector del pla

π donat que tant el punt P com el punt R són punts de π . Finalment calculem el pla π com el pla que passa pel punt ( )1,0, 1P = − i té com a

vectors directors ( )1,1, 2rv = −� i ( )4,0,1RP= −��

. Aquest pla és el següent:

( ) ( )1 1 4

: 1 0 0 1 8 4 1 0 1 7 4 4 0

1 2 1

x

y x y z y x y z

z

π− −

= → − + + + − = → − + + + = →+ −

: 7 4 3 0x y zπ→ + + + =

Finalment calculem la recta que ens demana l’enunciat, és a dir, la recta perpendicular al pla π que passa pel punt ( )2,1,1Q = .

Anomenem s a la recta buscada, aleshores tenim: ( )1,7,4ss v nππ⊥ → = =� � i

finalment les equacions paramètriques de la recta s seran:

2

: 1 7

1 4

x k

s y k k

z k

= + = + ∈ = +

ℝ

b) Calculeu el punt de la recta r que equidista dels punts P i Q.

Un punt genèric de la r té la forma ( )5 , , 2 2A k k k= + − − .

La distància d’aquest punt A als punts P i Q és el mòdul del vector que determinen. Així:

( ) ( ) ( )1,0, 1 5 , , 2 2 4 , ,1 2AP P A k k k k k k= − = − − + − − = − − − +��

( ) ( ) ( )2,1,1 5 , , 2 2 3 ,1 ,3 2AQ Q A k k k k k k= − = − + − − = − − − +��

( ) ( ) ( ) ( ), , 4 , ,1 2 3 ,1 ,3 2d A P d A Q AP AQ k k k k k k= → = → − − − + = − − − + →��



( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 2 2 24 1 2 3 1 3 2 xk k k k k k→ − − + − + + = − − + − + + →

( ) ( ) ( ) ( ) ( ) ( )2 2 2 2 2 24 1 2 3 1 3 2k k k k k k→ − − + − + + = − − + − + + →

2 216 8k k k→ + + + 21 4 4k k+ + + 29 6k k= + + 21 2k k+ − + 29 12 4k k+ + + → 1

12 17 16 19 17 19 16 12 2 42

k k k k k k⇒ + = + → − = − → − = → = −

Per tant, el punt buscat serà:

( )1

29 1

5 , , 2 2 , , 12 2

kA k k k A

−= − = + − − → = −

97) PAU 2016 Sèrie 1 Qüestió 6: Responeu a les qüestions següents: a) Calculeu l’equació cartesiana (és a dir, que té la forma Ax + By + Cz = D) del pla que passa pel punt de coordenades (0, 0, 1) i és perpendicular als plans 3x + y – z = 1 i x + y + 2z = 5. Sigui π el pla que busquem.

1π π⊥ → El vector normal a 1π serà vector director de π .

2π π⊥ → El vector normal a 2π serà vector director de π .

Per tant, en el nostre cas, ( )1 3,1, 1n = −� i ( )2 1,1,2n =� seran vectors directors de π .

Així podem calcular el pla π com el pla que passa pel punt ( )0,0,1 i té com a vectors directors

( )1 3,1, 1n = −� i ( )2 1,1,2n =� .

( ) ( )0 3 1 3 1

: 0 1 1 0 1 1 0 2 3 1 1 6 0

1 1 2 1 1 2

x x

y y x y z z x y

z z

π−− = → = → − + − − − + − = →− − − −

( )3 7 2 1 0 :3 7 2 2 0x y z x y zπ→ − + − = → − + − =

b) Suposeu que un pla 1π és perpendicular a un segon pla 2π i que el pla 2π és a la vegada

perpendicular a un tercer pla 3π . Expliqueu raonadament si necessàriament els plans 1π i 3π

han de ser perpendiculars entre ells. Agafem com a pla 1π el pla que conté

els eixos X i Y, és a dir, el pla 0z = . Agafem com a pla 2π el pla que conté

els eixos Y i Z, és a dir, el pla 0x = . Agafem com a pla 3π el pla 3y z+ = .



Podem observar que 1 2π π⊥ perquè el vector normal de 1π està contingut en el pla 2π .

També podem observar que 2 3π π⊥ perquè el vector normal de 2π està contingut en el pla

3π .

Però els plans 1π i 3π no són perpendiculars perquè el vector normal de 1π que és el vector

( )0,0,1 , és a dir, l’eix Z, no està contingut en el pla 3π .

NOTA 1: També es pot raonar analíticament. Dos plans són perpendiculars sii ho son els seus vectors normals. Dos vectors són perpendiculars sii el seu producte escalar dóna zero.

( )1 1: 0 0,0,1z nπ = → =�

( )2 2: 0 1,0,0x nπ = → =�

( )3 3: 3 0,1,1y z nπ + = → =�

( ) ( )1 2 1 20,0,1 1,0,0 0 0 0 0n n π π⋅ = ⋅ = + + = → ⊥� �

( ) ( )2 3 2 31,0,0 0,1,1 0 0 0 0n n π π⋅ = ⋅ = + + = → ⊥� �

Però ( ) ( )1 3 10,0,1 0,1,1 0 0 1 1 0n n π⋅ = ⋅ = + + = → → ⊥� �3π

NOTA 2: Una altra il·lustració gràfica encara més fàcil serien dos plans paral·lels tallats per un perpendicular comú. Per exemple agafant 1 : 0zπ =

2 : 3x yπ + = i 3 : 6zπ = podem observar que

1 2π π⊥ , que 2 3π π⊥ però 1π ⊥ 3π perquè de fet

1π i 3π són paral·lels.


A 3ℝ , siguin la recta r que té per equació ( ) ( ), , 1 , , 1x y z λ λ λ= + − i el pla π d’equació

2 2x y z− + = − .

a) Determineu la posició relativa de la recta r i el pla π .

( ) ( ) ( ) ( ) ( ) ( ): , , 1 , , 1 : , , 1,0,1 1,1, 1 1,1, 1rr x y z r x y z vλ λ λ λ= + − → = + − → = −�

( ): 2 2 : 2 2 0 2, 1,1x y z x y z nππ π− + = − → − + + = → = −�

( ) ( )1,1, 1 2, 1,1 2 1 1 0r rv n v nπ π⋅ = − ⋅ − = − − = → ⊥ →� � � � o bé r és paral·lela a π o bé r

està continguda en el pla π . Per saber en quin dels dos casos ens trobem agafem un punt de r i comprovem si pertany a π :

Sigui ( )1,0,1P r= ∈ aleshores 2 1 0 1 2 2 0 1 2 5 0 P rπ π⋅ − + + = − + + = ≠ → ∉ → �



NOTA: També podríem calcular la posició relativa entre la recta i el pla mitjançant la resolució del sistema format per les seves equacions generals. En aquest cas tindríem:

( ) ( ) 1 11 1: , , 1 , , 1

1 11 1 1

x y x yx y zr x y z

y z y zλ λ λ

− = − = − −= + − → = = → ≅ − = − + =−

Per tant el sistema format per la recta i el pla és:

1 2 2 2 122 2 2 1 1 2 1 1 0 1

1 ' 1 1 0 1 2 1 1 2

1 0 1 1 1 0 1 1 1

E E E E Ex y z

x y A

y z

↔ → −− + = − − − −

− = → = − ≅ − − ≅ + =

( ) ( )3 3 2

1 1 0 1 1 1 0 1

0 1 1 4 0 1 1 4 2 3 '

0 1 1 1 0 0 0 5

E E E

Rang A Rang A r iπ→ −

− − ≅ − ≅ − → = ≠ = →

no tenen cap punt en comú r π→ � b) Calculeu la distància entre la recta r i el pla π .

Nota: Podeu calcular la distància d’un punt de coordenades ( )0 0 0, ,x y z al pla d’equació


2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Com la recta r és paral·lela al pla π , la distància entre qualsevol punt de r i el pla π serà constant i coincidirà amb la distància entre r i π . És a dir:

( ) ( ) ( )( )22 2

2 1 0 1 21,0,1 , ,

2 1 1

rP r d r d Pπ π π⋅ − + +

= ∈ → = = =+ − +

�

2 0 1 2 5 5 5 6

64 1 1 6 6

− + += = = =

+ +

NOTA: En lloc d’aplicar una fórmula també es pot calcular el punt Q projecció perpendicular de

P sobre π i calcular ( ),d P Q .


Siguin a 3ℝ el pla π d’equació 2 2x y z− + = i els punts ( )3, 1,2A = − i ( )1,1, 2B = − .

a) Comproveu que els punts A i B són simètrics respecte del pla π .

Per veure que els dos punts A i B són simètrics respecte del pla π demostrarem que el

vector que formen AB��

és perpendicular al pla π i que el punt mitjà del segment AB és un punt de π .



Noteu que NO seria suficient demostrar que estan a la mateixa distància del pla tal i com mostra la figura.

( ) ( ) ( )1,1, 2 3, 1,2 2,2, 4AB B A= − = − − − = − −��

Aquest segment serà perpendicular al pla π si té la mateixa direcció que el vector normal al pla

nπ�

, és a dir, si els dos vectors són proporcionals. És evident que ( )2,2, 4AB = − −��

i ( )1, 1,2nπ = −� són proporcionals perquè 2AB nπ= −

�� .

Finalment demostrem que el punt mitjà del segment AB és un punt del pla. Calculem el punt mitjà mitjançant la fórmula:

( ) ( ) ( ) ( ) ( )1 13, 1,2 2,2, 4 3, 1,2 1,1, 2 2,0,0

2 2ABM A AB= + = − + − − = − + − − =

��

Aquest punt pertany al pla perquè compleix la seva equació, és a dir: 2 0 2 0 2− + ⋅ = . Aleshores podem assegurar que A i B són simètrics respecte del pla π .

NOTA: També haguéssim pogut demostrar que el vector AB��

és perpendicular al pla i desprès comprovar que la distància entre els dos punts i el pla és la mateixa.

b) Si r és la recta dels punts P que té per equació P B vλ= + , en què λ és un paràmetre

real i ( )1,1,0v =� , verifiqueu que els punts mitjans dels segments AP pertanyen al pla π .

Si ens imaginem la situació, donat que els punts A i B són simètrics respecte del pla π , per a que es compleixi la condició solament seria necessari que el vector director de la recta r fos paral·lel al pla, és a dir, és suficient

demostrar que ( )1,1,0v =� és perpendicular a

( )1, 1,2n = −�. Però ( ) ( )1, 1,2 1,1,0 1 1 0 0n v n v⋅ = − ⋅ = − + = → ⊥� � � �

.

● També podem resoldre el problema fent exactament el que ens marca l’enunciat tot i que evidentment és més llarg. Agafem un punt genèric de la recta :r

( ) ( ) ( ): 1,1, 2 1,1,0 1 ,1 , 2r P B v Pλ λ λ λ= + = − + → = + + −�

Calculem el punt mitjà del segment AP com la semisuma dels seus extrems:

( ) ( ) ( ) ( )2 2

3, 1,2 1 ,1 , 2 4 , , 02 , , 0

2 2 2

A PM λ λλ λ λ λ− + + + − ++= = = = +

Finalment comprovem que aquest punt mitjà ( )2 22 , , 0M λ λ= + pertany al pla π :

2 2: 2 2 0 2 2 0 2 0Mx y z Mλ λπ π− + − = → + − + ⋅ − = → ∈




Siguin les rectes ( ) ( ) ( ): , , 2,3, 3 1, 1,0r x y z λ= − + − i 3

: 5 22

xs y z

− = − = + .

a) Estudieu si les rectes r i s són paral·leles o perpendiculars.

( )1, 1,0rv = −� i ( )2,1,1sv =�

1 1

2 1 rv−≠ → � i sv

� no proporcionals r→ i s no són paral·leles.

( ) ( )1, 1,0 2,1,1 2 1 0 1 0r s rv v v⋅ = − ⋅ = − + = ≠ →� � � i sv�

no són perpendiculars r→ i s no són

perpendiculars Per tant, les rectes r i s no són ni paral·leles ni perpendiculars. b) Determineu la posició relativa de les rectes r i s i calculeu l’equació paramètrica de la recta t que talla perpendicularment la recta r i la recta s.

• Posició relativa de les rectes r i s:

( ) ( ) ( )( ) ( ) ( )

2 3 2 2 1 1: , , 2,3, 3 1, 1,0

3 5 3 4 1: , , 3,5, 2 2,1,1

3 2 1 1 1

r x y z

s x y z

λ µ λ λλλ µ λ λ

µ µ µ µ µ

+ = + + = = − = − + − → − = + → − = → = − → = − + − = − + → = − = − = −

Per tant, el sistema format per les dues rectes és compatible determinat i r i s es tallen en un punt que és:

( ) ( ) ( )( ) ( ) ( )

( ) ( )( ) ( ) ( )1

1

: , , 2,3, 3 1, 1,0 , , 1,4, 31,4, 3

: , , 3,5, 2 2,1,1 , , 1,4, 3

r x y z x y zP

s x y z x y zλµ

λµ

=−=−

= − + − = − → → = − = − + = −

NOTA: Una altra manera de saber la posició relativa entre les rectes r i s és fer el següent:

Agafem un punt de r , en aquest cas el més fàcil és el punt ( )2,3, 3A = − i un punt de s, en

aquest cas el més fàcil seria ( )3,5, 2B = − .

Construïm el vector ( ) ( ) ( )3,5, 2 2,3, 3 1,2,1AB B A= − = − − − =��

.

Si , , 0r sAB v v =

�� aleshores les rectes es tallen en un punt mentre que si , , 0r sAB v v ≠

��

aleshores les rectes es creuen. En aquest cas:

1 1 2

, , 2 1 1 1 0 1 2 0 2 0

1 0 1r sAB v v r = − = − + + + − − = →

�� i s es tallen.

Aquest mètode, en aquest cas, té l’inconvenient de que no ens dóna el punt de tall necessari per acabar el problema. • Equació paramètrica de la recta t que talla perpendicularment la recta r i la recta s.



Observant l’esquema de la dreta podem veure que la recta t buscada passarà pel punt P i

tindrà com a vector director tv�

un vector que ha de ser perpendicular a rv�

i a sv�

, per tant:

( )1 1 0 2 3 1, 1,3

2 1 1t r s

i j k

v v v i k k j i j k= × = − = − + + − = − − + = − −

��

� � ��

Finalment la recta t serà:

1

: 4

3 3

x k

t y k

z k

= − = − = − +

101) PAU 2017 Sèrie 1 Qüestió 2: a) Considereu els plans 1 : 5 7 1x y zπ − − = i 2 : 2 3 5x y zπ + + = .

Determineu l’equació general (és a dir, la que té la forma Ax By Cz D+ + = ) del pla que

passa per l’origen de coordenades i és perpendicular als plans 1π i 2π .

Sigui π el pla buscat.

1π π⊥ i 2π π⊥ aleshores 1

n nπ π⊥� � i

2n nπ π⊥� �

. Per tant, podem calcular nπ�

com el producte

vectorial dels vectors 1

nπ�

i 2

nπ�

.

Aleshores tenim que ( ) ( )1 2

5, 1, 7 2,3,1 5 1 7

2 3 1

i j k

n n nπ π π= × = − − × = − − =

��

� � �

( )15 14 2 21 5 20 19 17 20, 19, 17i k j k i j i j k= − + − + + − = − + = −� � ��

I si ha de passar per l’origen de coordenades aleshores 0D = obtenint que l’equació del pla buscat és:

: 20 19 17 0x y zπ − + =

b) Calculeu l’angle que formen els plans 1π i 2π .

L’angle entre els plans 1π i 2π serà el mateix que l’angle entre els seus vectors normals.

Calculem aquest últim angle mitjançant la definició de producte escalar.

cos cosu v

u v u vu v

α α ⋅⋅ = → =� �

� � � ��

En el nostre cas ( ) ( )( ) ( )

1 2

1 2

5, 1, 7 2, 3, 1cos

5, 1, 7 2, 3, 1

n n

n n

π π

π π

α⋅ − − ⋅

= = =− −

� �

� �

( ) ( )( )

2 22 2 2 2

10 3 7 00 cos 0 arcos 0

75 145 1 7 2 3 1α α− −= = = → = → = →

⋅+ − + − ⋅ + +

90ºα→ =




Considereu el pla : 1x y zπ + + = i la recta r que passa pels punts ( )0,0,6P = i

( )1,2,3Q =

a) Estudieu la posició relativa de la recta r i el pla π .

El vector director de la recta r és ( ) ( ) ( )1,2,3 0,0,6 1,2, 3rv PQ Q P= = − = − = −��

( ) ( )1,2, 3 1,1,1 1 2 3 0r rv n v nπ π⋅ = − ⋅ = + − = → ⊥ →� � � � O bé la recta i el pla són paral·lels o

bé la recta està inclosa en el pla. Per saber en quin dels dos casos ens trobem, agafem P r∈ i comprovem si aquest punt pertany a π .

( )0,0,6P r= ∈ i 0 0 6 6 1 P rπ+ + = ≠ → ∉ → paral·lela a π .

b) Calculeu la distància entre la recta r i el pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

: 1 : 1 0x y z x y zπ π+ + = → + + − =

( ) ( ) ( )( )2 2 2

0 0 6 1 5 5 5 3, , 0,0,6 , 1 0

33 31 1 1d r d P d x y zπ π

+ + −= = + + − = = = = =

+ +


A 3ℝ , siguin la recta

2:

2 4

x zr

y z

− = + =

i el punt ( )0,1, 1P = − .

a) Calculeu l’equació general (és a dir, la que té la forma Ax By Cz D+ + = ) del pla π

perpendicular a la recta r i que passa pel punt P .

rr n vππ ⊥ → =� �

( ) ( ) ( )1,0, 1 0,2,1 1 0 1 0 2 0 0 2 2 2 2, 1,2

0 2 1r

i j k

v i k j k i j i j k= − × = − = + − − + − = − + = −

��

� � ��

( ) ( ) ( )0,1, 12, 1,2 : 2 2 0 2 0 1 2 1 0Pn x y z D Dππ π = − ∈= − → − + + = → ⋅ − + ⋅ − + = →�

0 1 2 0 3 0 3 : 2 2 3 0D D D x y zπ→ − − + = → − + = → = → − + + =

b) Calculeu el punt simètric del punt P respecte del pla 3x y z+ + = − .

1) Calculem la recta r perpendicular al pla : 3x y zπ + + = − i que passa pel punt

( )0,1, 1P = − :



( )( ) ( ) ( ) ( )

1,1,1 0 1 1: , , 0,1, 1 1,1,1 :

1 1 10,1, 1

rr v n x y zr x y z r

P r

ππλ

⊥ → = = − − +→ = − + → = = →= − ∈

� �

1 1

: :1 1 2

x y x yr r

y z y z

= − − = − → ≅ − = + − =

2) Calculem el punt Q intersecció del pla π amb la recta r : Per fer-ho resolem el sistema d’equacions format per π i per r :

2 32 2 1

3 1 1 1 3 1 1 1 3

1 ' 1 1 0 1 0 2 1 2

2 0 1 1 2 0 1 1 2

F FF F Fx y z

x y A

y z

↔→ −+ + = − − −

− = − → = − − ≅ − − ≅ − = − −

3 3 221 1 1 3 1 1 1 3

0 1 1 2 0 1 1 2

0 2 1 2 0 0 3 6

F F F→ +− −

≅ − ≅ − − − −

3 6 2z z− = → = −

( )2 2 2 2 2 0y z y y y− = → − − = → + = → =

3 0 2 3 3 2 1x y z x x x+ + = − → + − = − → = − + → = −

Per tant, el punt Q intersecció entre la recta i el pla és ( ) ( ), , 1,0, 2x y z = − −

3) Finalment calculem el simètric de P que anomenarem 'P amb la fórmula 'P Q PQ= +��

:

( ) ( ) ( )1,0, 2 0,1, 1 1, 1, 1PQ Q P= − = − − − − = − − −��

( ) ( ) ( )' 1,0, 2 1, 1, 1 2, 1, 3P Q PQ= + = − − + − − − = − − −��


Sigui r la recta que passa pels punts ( )0,1,1A = i ( )1,1, 1B = − .

a) Trobeu l’equació paramètrica de la recta r .

El vector de la recta serà ( ) ( ) ( ) ( )1,1, 1 0,1,1 1,0, 2 1,0, 2rAB B A v= − = − − = − → = −��

Per tant, l’equació paramètrica de r serà:

0

: 1

1 2

x

r y

z

λ

λ

= + = = −

b) Calculeu tots els punts de la recta r que estan a la mateixa distància dels plans

1 : 2x yπ + = − i 2 : 1x zπ − = .





2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Per calcular els punts de r que equidisten dels plans 1π i 2π hem d’agafar un punt genèric de

r i notar que tal i com tenim expressats els plans no podem emprar la fórmula de la distància entre un punt i un pla perquè per emplear-la el terme independent ha d’estar a l’esquerra. Així:

1 1: 2 : 2 0x y x yπ π+ = − → + + = i 2 2: 1 : 1 0x z x zπ π− = → − − =

Un punt genèric de r serà: ( ), 1, 1 2P λ λ= − i aleshores:

( )1 2 2 2

1 2 3,

21 1 0d P

λ λπ

+ + += =

+ +

( ) ( )( )

2 22 2

1 2 1 1 2 1 3 2,

2 21 0 1d P

λ λ λ λ λπ

− − − − + − −= = =

+ + −

( ) ( ) ( )1 2

3 3 2, , 3 3 2 3 3 2

2 2d P d P

λ λπ π λ λ λ λ

+ −= → = → + = − → + = ± − →

52

14

3 3 2 5 2

3 3 2 4 1

λλ λ λλ λ λ λ −

=+ = − = → → → + = − + = − =

Amb 52λ = obtenim ( ) ( )5

2, 1, 1 2 , 1, 4P λ λ= − = −

Amb 14λ −= obtenim ( ) ( )31

4 2, 1, 1 2 , 1,P λ λ −= − =


Considereu els punts ( )3, 2,1P = − , ( )5,0,3Q = , ( )1,2,3R = i la recta 1 0

:2 3 5 0

x yr

y z

+ + = + − =

a) Determineu l’equació general (és a dir, que té la forma Ax By Cz D+ + = del pla que

passa per P i Q i és paral·lel a la recta r .

Sigui π el pla buscat. Com que P i Q són punts de π el vector PQ��

serà vector director de π . Com que π és paral·lel a la recta r el vector director de r també serà vector director de π .

( ) ( ) ( ) 25,0,3 3, 2,1 2,2,2PQ Q P ÷= − = − − = →��

Podem agafar com a vector

( )1,1,1PQ=��

Càlcul del vector director de la recta r :



( ) ( ) ( )1,1,0 0,2,3 1 1 0 3 3 2 3, 3,2

0 2 3r

i j k

v i j k= × = = − + = −

��

��

Finalment calculem el pla π com el pla que passa pel punt ( )3, 2,1P = − i té com a vectors

directors ( )1,1,1PQ=��

i ( )3, 3,2rv = −�.

( ) ( ) ( )3 1 3

: 2 1 3 0 5 3 2 6 1 0

1 1 2

x

y x y z

z

π−+ − = → ⋅ − + + − ⋅ − = →−

5 15 2 6 6 0 :5 6 7 0x y z x y zπ→ − + + − + = → + − − =

b) Donats el pla 2 7x y mz+ + = i el pla que passa per P , Q i R , trobeu m perquè siguin

paral·lels i no coincidents. Primer calculem el pla π que passa pels punts P , Q i R com el pla que passa pel punt P i

té com a vectors directors PQ��

i PR��

.

( ) ( ) ( ) 25,0,3 3, 2,1 2,2,2PQ Q P ÷= − = − − = →��

Podem agafar ( )1,1,1PQ=��

( ) ( ) ( ) 21,2,3 3, 2,1 2,4,2PR R P ÷= − = − − = − →��

Podem agafar ( )1,2,1PR= −��

Per tant: ( ) ( ) ( )3 1 1

: 2 1 2 0 3 2 2 3 1 0

1 1 1

x

y x y z

z

π− −+ = → − − − ⋅ + + ⋅ − = →−

3 2 4 3 3 0 : 2 3 4 0x y z x y zπ→ − + − − + − = → − − + − =

NOTA: Dos plans : 0Ax By Cz Dπ + + + = i ' : ' ' ' ' 0A x B y C z Dπ + + + = són paral·lels si

' ' ' '

A B C D

A B C D= = ≠

En el nostre cas : 2 3 4 0x y zπ − − + − = i ' : 2 7 0x y mzπ + + − = seran paral·lels sii

1 2 3 4 1 33 3

1 2 7 1m m

m m

− − − −= = ≠ → = → − = → = −−


Considereu el pla que té com a vectors directors ( )1,3,2u = − i ( )2,1,0v = i que passa pel

punt ( )1,0,3A = .

a) Calculeu l’equació de la recta que és perpendicular al pla i passa pel punt A. L’equació del pla serà:



( ) ( ) ( ) ( ) ( )1 1 2

: 3 1 0 1 2 4 3 7 0

3 2 0

x

y x y z

z

π− −

= → − ⋅ − − ⋅ − + − ⋅ − = →−

( )12 2 4 7 21 0 2 4 7 23 0 : 2 4 7 23 0xx y z x y z x y zπ−→ − + + − + = → − + − + = → − + − =

Sigui r la recta que hem de calcular.

Com que r π⊥ aleshores ( )2, 4,7rv nπ= = −� �

Com r passa per ( )1,0,3A = tenim que l’equació vectorial de r serà:

( ) ( ) ( ): , , 1,0,3 2, 4,7r x y z λ= + −

b) Calculeu la distància del punt ( )1,5,0P = al pla.



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Substituint el punt ( )1,5,0P = i el pla : 2 4 7 23 0x y zπ − + − = en la fórmula

( ) 0 0 0

2 2 2,

Ax By Cz Dd P

A B Cπ

+ + +=

+ + obtenim que:

( )( )

2

22 2

2 1 4 5 7 0 23 2 20 0 23 41 41 41 69, 4,94

694 16 49 69 692 4 7d P uπ

⋅ − ⋅ + ⋅ − − + − −= = = = =

+ ++ − +≃


Considereu els punts de l’espai tridimensional ( )1,1,0A = , ( )3,5,0B = i ( )1,0,0C = i la

recta : 12

zr x y= − = .

a) Trobeu el punt d’intersecció de la recta r amb el pla que passa pels punts A, B i C .

Per poder calcular la intersecció del pla i la recta prèviament hem de calcular l’equació del pla. ● Càlcul del pla π que passa pels punts A, B i C .

π serà el pla que passa pel punt A i té vectors directors AB��

i AC��

.

( ) ( ) ( )3,5,0 1,1,0 2,4,0AB B A= − = − =��

( ) ( ) ( )1,0,0 1,1,0 0, 1,0AC C A= − = − = −��

Noteu que per calcular l’equació de π podríem agafar vectors proporcionals a AB��

i a AC��

donat que el primer es pot dividir entre 2 i el segon entre 1− . Per tant:



( ) ( )2

1 2 0

: 1 4 1 0 2 0 2 0 : 0

0 0

x

y z z z

z

π π÷ −

−− − = → ⋅ − = → − = → =

Per tant el pla π és el pla horitzontal que conté els eixos OX i OY, 0z = .

● Càlcul del punt d’intersecció entre la recta : 12

zr x y= − = i el pla : 0zπ =

( )

1 1: 1 :

2 12 12

x y x yzr x y rz

y zy

= − = − = − = → ≅ ⋅ − =− =

Que intersectada amb el pla 0z = tindrem:

( )0 2 1 0 1 0 1z y y y= → ⋅ − = → − = → =

1 1 1 0 0x y x= − = − = → =

Per tant el punt d’intersecció és ( ) ( ), , 0,1,0x y z =

b) Trobeu els punts P de la recta r per als quals el tetraedre de vèrtexs P, A, B i C té un

volum de 32u . NOTA: El volum d’un tetraedre de vèrtexs P , Q , R i S es pot calcular amb l’expressió

( )1det , ,

6PQ PR PS��

.

Per poder trobar el punt P de la recta r que compleixi la condició que ens demanen agafarem un punt genèric de la recta.

( )( ) ( ) ( ) ( )0,1,0

: 1 : , , 0,1,0 1,1,22 1,1,2r

A rzr x y r x y z

vλ

= ∈= − = → → = +=�

Així un punt genèric de r serà: ( ), 1, 2P λ λ λ= +

Finalment calcularem el volum del tetraedre de vèrtexs P , A, B i C mitjançant la fórmula que ens proporcionen en l’enunciat del problema. Com que el punt P té l’expressió més complicada de tots, enlloc d’agafar-lo com a referència i

calcular els vectors PA��

, PB��

i PC��

, agafarem com a origen el punt C i calcularem els vectors

CA��

, CB��

i CP��

. Aleshores obtindrem:

( ) ( ) ( )1,1,0 1,0,0 0,1,0CA A C= − = − =��

( ) ( ) ( )3,5,0 1,0,0 2,5,0CB B C= − = − =��

( ) ( ) ( ), 1, 2 1,0,0 1, 1, 2CP P C λ λ λ λ λ λ= − = + − = − +��



Calculem el volum del tetraedre:

( )0 2 1

2 1det , , 1 5 1 1 1 4 4

0 20 0 2

CA CB CP

λλ

λ λ λλ

λ

−−

= + = − ⋅ = − ⋅ = −��

( )1 1det , , 4

6 6V CA CB CP λ= = −

��

4 12 312 4 2 4 12 3

4 12 36V

λ λλ λ λ

λ λ− = = −

= → − = → − = → → → = ± − = − =

Substituint els valors de λ en el punt genèric ( ), 1, 2P λ λ λ= + obtenim:

( ) ( )3 3, 3 1, 2 3 3,4,6Pλ = → = + ⋅ =

( )( ) ( )3 ' 3, 3 1, 2 3 3, 2, 6Pλ = − → = − − + ⋅ − = − − −

Per tant hi ha dos punts de r que compleixen la condició del volum.

Són ( )3,4,6P = i ( )' 3, 2, 6P = − − −




Siguin el pla d’equació : 0x y zπ + − = i el punt ( )2,3,2P = .

a) Calculeu el punt simètric del punt P respecte del pla π .

Tal i com mostra la figura per calcular el punt 'P simètric del punt P respecte del pla π calcularem: 1) La recta r perpendicular al pla π que passa pel punt P. 2) El punt de tall A entre la recta r i el pla π .

3) El punt 'P com 'P A PA= +��

. 1) Comencem aleshores amb la recta r perpendicular al pla π que passa pel punt P.

( )1,1, 1rr v nππ⊥ → = = −� �

( ) ( ) ( ) ( )2,3,2 : , , 2,3,2 1,1, 1P r r x y z λ= ∈ → = + −

2) Calculem el punt de tall A entre la recta r i el pla π . Per poder calcular el punt de tall necessitem expressar la recta r amb la seva equació general per plantejar un sistema.

( ) ( ) ( ) ( )( )

2 22 3 2: , , 2,3,2 1,1, 1

1 1 1 3 2

x zx y zr x y z

y zλ

− − = −− − − = + − → = = → →− − − = −

2 2 4:

3 2 5

x z x zr

y z y z

− + = − = + → → − + = − = +

Per tant el sistema format per π i r serà:

0

4

5

x y z

x z

y z

+ − = + = + =

3 3 22 2 1

1 1 1 0 1 1 1 0 1 1 1 0

' 1 0 1 4 0 1 2 4 0 1 2 4

0 1 1 5 0 1 1 5 0 0 3 9

F F FF F F

A→ +→ −

− − − = ≅ − ≅ −

3 9 3z z= → =

2 4 2 3 4 6 4 2 2y z y y y y− + = → − + ⋅ = → − + = → − = − → =

0 2 3 0 1 0 1x y z x x x+ − = → + − = → − = → =

Per tant el punt de tall és ( )1,2,3A =

3) Finalment calculem el punt 'P com 'P A PA= +��

:

( ) ( ) ( )1,2,3 2,3,2 1, 1,1PA A P= − = − = − −��

( ) ( ) ( ) ( )' 1,2,3 1, 1,1 0,1,4 ' 0,1,4P A PA P= + = + − − = → =��



b) Calculeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = ) dels dos plans

paral·lels a π que estan a una distància 3 del punt P.



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Els plans paral·lels al pla : 0x y zπ + − = seran de la forma ' : ' 0x y z Dπ + − + =

Donat que volem que la distància d’aquests plans al punt P sigui 3 tindrem:

( ) ( )( )( )22 2

2 3 2 '', 3 ' : ' 0, 2,3,2 3 3

1 1 1

Dd P d x y z D Pπ π

+ − += → + − + = = → = →

+ + −

3 ' 3 ' 03 '3 3 ' 3 3 ' 3

3 ' 3 ' 63

D DDD D

D D

+ = =+ → = → + = → + = ± → → + = − = −

Tal i com mostra la figura adjunta, donats el pla π i el punt P hi haurà dos plans paral·lels a π que estiguin a una distància determinada del punt P (un per sota i l’altre per

sobre de P ). En aquest cas són: ' : 0x y zπ + − = que

casualment coincideix amb el pla π del primer apartat i el pla

'' : 6 0x y zπ + − − = .


Siguin les rectes 1

2: 1 5

1

yr x z

−− = = −−

i ( ) ( )2 : , , 2 3 , 1 ,2r x y z λ λ= − − + .

a) Trobeu l’equació cartesiana (és a dir, que té la forma Ax By Cz D+ + = ) del pla que conté

la recta 1r i és paral·lel a la recta 2r .

Per definir un pla necessitem un punt i dos vectors directors. Sigui π el pla buscat.

Com que la recta 1r està continguda en el pla π aleshores el punt ( )1,2,5A = de r també

serà un punt de π i el vector director de 1r , ( )1 1, 1,1v = −� serà vector director de π .

Com que π és paral·lel a la recta 2r aleshores el vector director de 2r , ( )2 3,1,0v = −� serà

vector director de π .

Per tant ja podem calcular π com el pla que passa per ( )1,2,5A = i té vectors directors

( )1 1, 1,1v = −� i ( )2 3,1,0v = −�

.



( ) ( ) ( ) ( ) ( )1 1 3

: 2 1 1 0 1 1 2 3 5 2 0

5 1 0

x

y x y z

z

π− −− − = → − ⋅ − − − ⋅ + − ⋅ − = →−

( )11 3 6 2 10 0 3 2 17 0 : 3 2 17 0xx y z x y z x y zπ−→ − + − + − + = → − − − + = → + + − =

b) Digueu quina condició s’ha de complir perquè existeixi un pla que contingui la recta 1r i sigui

perpendicular a la recta 2r . Amb les rectes 1r i 2r de l’enunciat, comproveu si existeix un pla

que contingui la recta 1r i sigui perpendicular a la recta 2r .

Anomenem π al pla buscat.

És més fàcil raonar en ordre invers. Si π és perpendicular a la recta 2r està clar que el vector

director de 2r és el vector normal de π . Això ens donaria la

següent construcció: Si ara afegim que el pla π contingui la recta 1r hem de poder “acoplar” 1r dintre del pla, i això

solament ho podrem fer si 1r és perpendicular a 2r . Per tant, les

dues rectes han de ser perpendiculars. Noteu que la recta 1r la podem girar per dintre del pla però no

aixecar-la de manera que deixi d’estar continguda en el pla. Per tant, totes les rectes 1r vàl·lides són perpendiculars a 2r tal i com

mostra el dibuix de la dreta. Finalment, per comprovar si amb les rectes de l’enunciat existeix aquest tipus de pla hem de comprovar si les rectes són perpendiculars, és a dir, si el producte escalar dels seus vectors directors dóna zero.

( )1 1

2: 1 5 1, 1,1

1

yr x z v

−− = = − → = −−

�

( ) ( ) ( )2 2: , , 2 3 , 1 ,2 3,1,0r x y z vλ λ= − − + → = −�

( ) ( )1 2 11, 1,1 3,1,0 3 1 0 4 0v v r⋅ = − ⋅ − = − − + = − ≠ →� � i 2r no són perpendiculars i per tant en

aquest cas no existeix aquest tipus de pla. 110) PAU 2019 Sèrie 1 Qüestió 3:

Un dron es troba en el punt ( )2, 3,1P = − i volem dirigir-lo en línia recta fins al punt més

proper del pla d’equació : 3 4 15 0x zπ + + = .



a) Calculeu l’equació de la recta, en forma paramètrica, que ha de seguir el dron. Quina distància ha de recórrer fins a arribar al pla? La recta que seguirà el dron és la perpendicular al pla que passa per P. Per tant, hem de calcular la recta perpendicular al pla

: 3 4 15 0x zπ + + = que passa pel punt ( )2, 3,1P = − .

Sigui r la recta buscada. Tenim que el vector director de r

serà el vector normal de π . Per tant, ( )3,0,4rv nπ= =� �.

Com que sabem que el punt P és un punt de r aleshores l’equació vectorial de r serà:

( ) ( ) ( ): , , 2, 3,1 3,0,4r x y z λ= − + i per tant la paramètrica:

2 3

: 3

1 4

x

r y

z

λ

λ

= + = − = +

La distància que ha de recórrer el dron és la distància que el separa del pla, és a dir:

( ) ( )( )2 2 2

3 2 4 1 15 6 4 15, 2, 3,1 , :3 4 15 0

9 0 163 0 4d P d x zπ π

⋅ + ⋅ + + += − + + = = = =

+ ++ +

25 255

525= = =

b) Trobeu les coordenades del punt del pla on arribarà el dron.



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

El punt del pla on arribarà el dron és la intersecció Q entre la recta r i el pla π .

Calculem per tant la intersecció entre la recta

2 3

: 3

1 4

x

r y

z

λ

λ

= + = − = +

i

el pla : 3 4 15 0x zπ + + = . Per crear el sistema d’equacions, en primer lloc hem de passar la recta r a la seva equació general:

( ) ( )2

3 2 13 4

14

2 3 2 34 2 3 1

: 3 3 33 3

1 4 1 4

x

x z

z

x xx z

r y y yy y

z z

λλ λ

λ λ λ

−− −

−

== + − = = ⋅ − = ⋅ − = − → = − → = − → → →

= − = − = + − = =



4 8 3 3 4 3 5

3 3

x z x z

y y

− = − − = → → = − = −


1 1

2 2

4

3

4 3 5 4 3 5 16 12 204 3 5:

3 3 4 15 9 12 453

3 4 15 3 3: 3 4 15 0

F F

F F

x z x z x zx zr

y x z x zy

x z y yx zπ

→

→

− = − = − = − = ≅ = − ≅ + = − ≅ + = −= − + = − = − = −+ + =

Sumant les dues primeres equacions obtenim que 25 25x = − i per tant 1x = −

Substituint en l’equació ( )14 3 5 4 1 3 5 4 3 5xx z z z=−− = → ⋅ − − = → − − = →

3 5 4 3 9 3z z z→ − = + → − = → = −

I per tant el punt de tall entre la recta i el pla serà: ( )1, 3, 3Q = − − −

NOTA: Una manera molt original de trobar el punt Q és aprofitar que en un moment de l’exercici hem expressat la recta r mitjançant les seves equacions paramètriques.

Recuperant aquestes equacions tenim:

2 3

: 3

1 4

x

r y

z

λ

λ

= + = − = +

Això vol dir que qualsevol punt de la recta r és de la forma ( )2 3 , 3,1 4λ λ+ − + .

Si volem intersecar la recta amb el pla : 3 4 15 0x zπ + + = només necessitem substituir:

( ) ( )3 2 3 4 1 4 15 0 6 9 4 16 15 0 25 25 0 1λ λ λ λ λ λ⋅ + + ⋅ + + = → + + + + = → + = → = −

I per tant:

( ) ( )12 3 , 3, 1 4 1, 3, 3Qλλ λ =−+ − + → = − − −


Siguin la recta 2

:1

xr

y z

= − =

i el pla : 3x zπ − = .

a) Calculeu l’equació paramètrica de la recta que és perpendicular al pla π i que el talla en el mateix punt en què el talla la recta r. Primer haurem de calcular el punt de tall entre la recta r i el pla π :

22:

11

3: 3

xxr

y zy z

x zx zπ

= = ≅ − =− = − =− =

23 2 3 2 3 1xx z z z z=− = → − = → − = → = −

( )11 1 1 1 1 0zy z y y y=−− = → − − = → + = → =

Per tant, el punt de tall entre r i π és ( )2,0, 1P = −



Ara hem de calcular l’equació paramètrica de la recta s perpendicular a : 3x zπ − = i que

passa pel punt ( )2,0, 1P = − .

( ) ( ) ( ) ( )2

1,0, 1 : , , 2,0, 1 1,0, 1 : 0

1s

x

s v n s x y z s y

zπ

λπ λ

λ

= +⊥ → = = − → = − + − → = = − −

� �

b) Trobeu els punts de r que estan a una distància de 8 unitats del pla π .



2 2 2

Ax By Cz D

A B C

+ + +

+ +.

Buscarem un punt genèric de la recta r i obligarem a que la distància d’aquest punt al pla π

sigui 8 .

( ) ( )2 2 2: , , 2, 1 ,

1 1 1zx x x

r x y zy z y y

λ λ λλ λ

== = = → → → = + − = − = = +

Sigui ( )2, 1 ,P λ λ= + un punt genèric de r, obliguem ara a que la distància entre P i el pla

π sigui 8 .

( ) ( )( ), 8 2, 1 , , : 3 8d P d x zπ λ λ π= → + − = = →

( )( )( )22 2

2 3 12, 1 , , : 3 0 8 8 8

1 0 11 0 1d x z

λ λλ λ π

− − − −→ + − − = = → = → = →

+ ++ + −

1 418 1 8 2 1 4 1 4

1 42

λλλ λ λ

λ− − =− −

→ = → − − = ⋅ → − − = → − − = ± → →− − = −

( ) ( )( )

2, 1 , 2, 4, 51 4 5

1 4 3 2, 4, 3P P

Qλ λλ λ

λ λ= + = − −− − = = − → → → − + = = =

NOTA: Cal vigilar amb la forma en que ens donin el pla. Per poder utilitzar la fórmula de la

distància entre un punt ( )0 0 0, ,P x y z= i un pla : 0Ax B Dy Czπ + + + = necessitem que

tots els termes de π estiguin a l’esquerra de l’igual, és a dir, si utilitzéssim π expressat com : Ax By Cz Dπ + + = − el raonament seria incorrecte.

112) PAU 2019 Sèrie 4 Qüestió 5: Considereu els plans 1 : 2 5x ay zπ + + = , 2 : 1x ay zπ + + = i

( ) ( )3 : 2 1 1 0x a y a zπ + + + + = , en què a és un paràmetre real.

a) Estudieu per a quins valors del paràmetre a els tres plans es tallen en un punt.

Els plans es tallaran en un únic punt sii el sistema que formen és compatible determinat. Estudiem la matriu ampliada del sistema.



2 1 5

' 1 1 1

2 1 1 0

a

A a

a a

= + +

Aprofitant que la matriu de coeficients és quadrada treballarem per determinants.

( ) ( )Desenvolupant3a fila

2 11 2 1 2

1 1 2 1 11 1 1 1

2 1 1

aa a

A a A a aa a

a a

= → = ⋅ − + + + = + +

( ) ( ) 2 22 0 1 1 1 0 1 1a a a a a a a= ⋅ − + ⋅ + + ⋅ = − − + + = −

2 20 1 0 1 1 1A a a a a= ↔ − = ↔ = ↔ = ↔ = ±

Per tant els 3 plans es tallaran en un únic punt sempre que a sigui diferent de 1 i de -1.

b) Comproveu que per al cas 1a = la interpretació geomètrica del sistema format per les equacions dels tres plans és la que es mostra en la imatge següent:

1

2 1 5 2 1 1 5

' 1 1 1 ' 1 1 1 1

2 1 1 0 2 2 2 0

a

a

A a A

a a

=

= → = ≅ + +

( ) ( )1 2 2 2 1

3 3 1

2

2

1 1 1 1 1 1 1 1

2 1 1 5 0 1 1 3 2 3 ' . .

2 2 2 0 0 0 0 2

F F F F F

F F FRang A Rang A S I

↔ → −

→ −

≅ ≅ − − → = ≠ = → → −

→ Els tres plans no tenen cap punt en comú. Hi ha 4 posicions relatives entre 3 plans de manera que no tinguin cap punt en comú, són les següents:

Cas 1 Cas 2 Cas 3 Cas 4

Tres plans paral·lels Dos plans coincidents paral·lels a un tercer

Dos plans paral·lels i l’altre oblicu

Tres plans que es tallen 2 a 2 formant rectes

paral·leles

En els dos primers casos el paral·lelisme entre tots tres plans fa que ( ) 1Rang A = . Com que

en el nostre cas ( ) 2Rang A = podem descartar aquests dos casos.



Per tant ens queda saber si ens trobem en el cas 3 o en el cas 4. Ens hem de plantejar... ¿què diferencia aquests dos casos? La resposta és òbvia, en el cas 3 existeixen plans paral·lels i en el cas 4 no. Per tant ens preguntem: Existeixen plans paral·lels? Noteu que l’existència de plans paral·lels l’hem de mirar a la matriu 'A original perquè les transformacions Gaussianes roten els plans i per tant trenquen el paral·lelisme.

2 1 1 5

' 1 1 1 1

2 2 2 0

A

=

on podem observar que les files 2 i 3 corresponen a plans paral·lels

perquè 1 1 1 1

2 2 2 0= = ≠ . Per tant, estem en el cas 3 que és el que correspon amb la figura

proposada.

Recull de problemes de selectivitat sobre geometria afí i mètrica · 2019-10-14 · 2) PAU LOGSE...

Documents

Transcript of Recull de problemes de selectivitat sobre geometria afí i mètrica · 2019-10-14 · 2) PAU LOGSE...